Aufgabe 3.4Z: GSM–Vollraten–Sprachcodec

• Zurück zum Buch

LPC-, LTP- und RPE-Parameter beim GSM-Vollraten-Codec

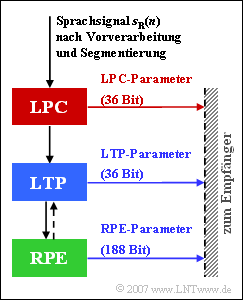
Dieser 1991 für das GSM–System standardisierte Codec – dieses Kunstwort steht für eine gemeinsame Realisierung von Coder und Decoder – mit der englischen Bezeichnung GSM Fullrate Vocoder kombiniert drei Methoden zur Kompression von Sprachsignalen:

• Linear Predictive Coding (LPC),
• Long Term Prediction (LTP), und
• Regular Pulse Excitation (RPE).

Die in der Grafik angegebenen Zahlen geben die Bitzahl an, die von den drei Einheiten dieses FR–Sprachcodecs pro Rahmen von jeweils $20$ Millisekunden Dauer generiert werden.

Anzumerken ist dabei, dass LTP und RPE im Gegensatz zu LPC nicht rahmenweise, sondern mit Unterblöcken von $5$ Millisekunden arbeiten. Dies hat jedoch keinen Einfluss auf die Lösung der Aufgabe.

Das Eingangssignal in obiger Grafik ist das digitalisierte Sprachsignal $s_{\rm R}(n)$. Dieses entsteht aus dem analogen Sprachsignal $s(t)$ durch

• eine geeignete Begrenzung auf die Bandbreite $B$,
• Abtastung mit der Abtastrate $f_{\rm A} = 8 \ \rm kHz$,
• Quantisierung mit $13 \ \rm Bit$,
• anschließender Segmentierung in Blöcke zu je $20 \ \rm ms$.

Auf die weiteren Aufgaben der Vorverarbeitung soll hier nicht näher eingegangen werden.

Hinweis:

Diese Aufgabe gehört zum Themengebiet „Sprachcodierung” im Gemeinsamkeiten von GSM und UMTS dieses Buches sowie zum Sprachcodierung des Buches „Beispiele von Nachrichtensystemen”.

Fragebogen

1

Auf welche Bandbreite muss das Sprachsignal begrenzt werden?

$B \ = \ $ $\ \rm kHz$

2

Aus wie vielen Abtastwerten $(N_{\rm R})$ besteht ein Sprachrahmen? Wie groß ist die Eingangsdatenrate $R_{\rm In}$?

$N_{\rm R} \ = \ $ $\ \rm Abtastwerte$

$R_{\rm In} \ = \ $ $\ \rm kbit/s$

3

Wie groß ist die Ausgangsdatenrate $R_{\rm Out}$ des GSM-Vollraten-Codecs?

$R_{\rm Out} \ = \ $ $\ \rm kbit/s$

4

Welche Aussagen treffen hinsichtlich des Blocks „LPC” zu?

	LPC macht eine Kurzzeitprädiktion über eine Millisekunde.
	Die $36$ LPC–Bits geben Koeffizienten an, die der Empfänger nutzt, um die LPC–Filterung rückgängig zu machen.
	Das Filter zur Kurzzeitprädiktion ist rekursiv.
	Das LPC–Ausgangssignal ist identisch mit dem Eingang $s_{\rm R}(t)$.

5

Multiple-Choice Frage

	Falsch
	Richtig

6

Multiple-Choice Frage

	Falsch
	Richtig

Musterlösung

Musterlösung

(1)  (2)  (3)  (4)  (5)  (6)