Aufgabe 3.13: Nochmals zu den Pfadgewichtsfunktionen

Zur Reduktion des Zustandsübergangsdiagramms

Auf der Seite 4c des Theorieteils zu Kapitel 3.5 wurde für das Beispiel unseres Rate–1/2–Standardcodes mit Gedächtnis $m = 2$ und der Übertragungsfunktionsmatrix

$${\boldsymbol{\rm G}}(D) = \big ( 1 + D + D^2\hspace{0.05cm},\hspace{0.1cm} 1 + D^2 \hspace{0.05cm}\big )$$

die Berechnung der Pfadgewichtsfunktionen sehr ausführlich beschrieben. Als Ergebnisse wurden genannt:

$$T_{\rm enh}(X, U) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{U\hspace{-0.05cm} X^5}{1- 2U\hspace{-0.05cm}X} =$$

$$\ = \ \hspace{-0.2cm} U\hspace{-0.05cm}X^5 \cdot \left [ 1 + (2U\hspace{-0.08cm}X) + (2U\hspace{-0.08cm}X)^2 + ... \hspace{0.05cm} \right ] \hspace{0.01cm},$$

$$T(X) \hspace{-0.2cm} \ = \ \hspace{-0.2cm} \frac{X^5}{1- 2X} =$$

$$\ = \ \hspace{-0.2cm} X^5 \cdot \left [ 1 + (2X) + (2X)^2 + ... \hspace{0.05cm} \right ] \hspace{0.05cm}.$$

Nun sollen die gleichen Berechnungen für den Äquivalenten systematischen Code mit der Übertragungsfunktionsmatrix

$${\boldsymbol{\rm G}}(D) = \big ( 1 \hspace{0.05cm},\hspace{0.1cm} (1 + D^2)/(1 + D + D^2) \hspace{0.05cm}\big )$$

durchgeführt werden.

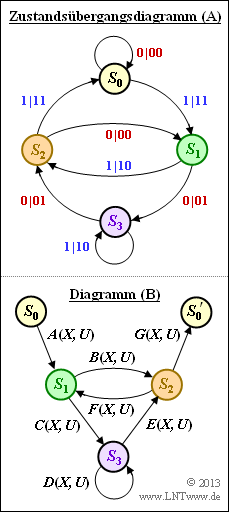
Die Grafik zeigt das Zustandsübergangsdiagramm (A) und die Struktur des reduzierten Diagramms (B), wobei die Übergänge mit $A(X, \, U), \ ... \ , \ G(X, \, U)$ allgemein bezeichnet sind. In der Teilaufgabe (1) sollen diese Abkürzungen an das Zustandsübergangsdiagramm (A) angepasst werden.

Hinweis:

Die Aufgabe bezieht sich auf das Kapitel Distanzeigenschaften und Fehlerwahrscheinlichkeitsschranken.
Zur Lösung der Teilaufgaben (b) und (c) verweisen wir hier nochmals auf die Seite 4c im Theorieteil.

Fragebogen

Musterlösung

(1) (2) (3) (4) (5)

	correct
	false

	correct
	false