Aufgabe 2.6: Zyklisches Präfix

DSL/DMT mit zyklischem Präfix

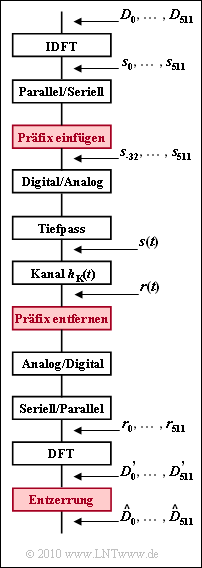
Ein wesentlicher Vorteil von DSL/DMT ist die einfache Entzerrung von Kanalverzerrungen durch die Einfügung eines Guard–Intervalls und eines zyklischen Präfix. Die Grafik zeigt ein vereinfachendes Blockschaltbild, wobei die zur Entzerrung des Kanalfrequenzgangs

$$H_{\rm K}(f) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} h_{\rm K}(t)$$

erforderlichen Komponenten rot hervorgehoben sind.

Für den ADSL/DMT–Downstream gelten folgende Parameter:

Mit jedem Rahmen werden die Subkanäle $k = 64, ... , 255$ bei den Trägerfrequenzen $f_k = k \cdot f_0$ mit den QAM–Symbolen $D_k$ belegt. Wegen der Reservierung der untersten Frequenzen für ISDN und Upstream gilt $D_0 = ... D_{63} = 0$.

Die Grundfrequenz ist zu $f_0 = 4.3125 \ \rm kHz$ gewählt und die Rahmendauer beträgt $T = 1/f_0 \approx 232 \ {\rm\mu s}$. Diese Werte ergeben sich aus der Forderung, dass pro Sekunde $4000$ Rahmen übertragen werden sollen und nach jedem $68$. Rahmen ein Synchronisationsrahmen eingefügt wird.

Nach Belegung der oberen Koeffizienten $(k = 257, ... , 448)$ gemäß $D_k = D_{512–k}^{\ast}$ wird der gesamte Block $D_0, ... , D_{511}$ einer Inversen Diskreten Fouriertransformation (IDFT) zugeführt. Die Zeitkoeffizienten sind dann $s_0, ... , s_{511}$.

Um Impulsinterferenzen – auch Inter–Symbol–Interferenzen (ISI) genannt – zwischen benachbarten Rahmen zu vermeiden, wird zwischen zwei Rahmen ein Schutzabstand („Guard–Intervall”) der Dauer $T_{\rm G}$ eingefügt. Der Rahmenabstand muss dabei mindestens so groß sein wie die Länge $T_{\rm K}$der Impulsantwort.

Zudem werden die IDFT–Ausgangswerte $(s_{480}, ... , s_{511})$ dupliziert, als $(s_{–32}, ..., s_{–1})$ dem Ausgangsvektor $(s_0, ... , s_{511})$ vorangestellt und im Guard–Intervall übertragen. Man nennt dies das „zyklische Präfix”. Somit stören sich auch die Subträger eines Rahmens nicht, das heißt, es gibt nicht nur keine ISI, sondern auch keine Inter–Carrier–Interferenzen (ICI).

Hinweis:

Die Aufgabe bezeiht sich auf die letzte Seite von Kapitel 2.4. Im Fragebogen bezeichnet $s_k(t)$ den (zeitkontinuierlichen) Signalverlauf, wenn allein der Koeffizient $D_k$ des Trägers bei $f_k = k \cdot f_0$ von $0$ verschieden ist.

Fragebogen

$T_{\rm G} \ = \ $

$ \ \rm \mu s$

$T_{\rm K, \ max} \ = \ $

$ \ \rm \mu s$

	Alle Spektralkoeffizienten nach der DFT $(D_k')$ sind gleich $D_k$.
	Die Koeffizienten nach Entzerrung ($D_k$ mit ^) sind gleich $D_k$.
	Das Guard–Intervall hat keine Auswirkung auf die Datenrate.

	Das würde nichts verbessern.
	Daten verschiedener Rahmen stören sich nicht gegenseitig.
	Daten innerhalb eines Rahmens stören sich nicht gegenseitig.

	Der Einfluss von $h_K(t)$ wird auf $t < 0$ begrenzt.
	Für $0 ≤ t ≤ T$ stellt $s_k(t)$ eine harmonische Schwingung dar.
	$h_{\rm K}(t)$ hat keinen Einfluss auf Betrag und Phase von $s_k(t)$.

Musterlösung

(1)