Binomial and Poisson Distribution (Applet)

Applet Description

This applet allows the calculation and graphic display of

• the probabilities ${\rm Pr}(z=\mu)$ of a discrete random variable $z \in \{\mu \} = \{0, 1, 2, 3, \text{...} \}$, that determine its Probability Density Function (PDF) (graphic representation with Dirac functions ${\rm \delta}( z-\mu)$):

$$f_{z}(z)=\sum_{\mu=1}^{M}{\rm Pr}(z=\mu)\cdot {\rm \delta}( z-\mu),$$

• the probabilities ${\rm Pr}(z \le \mu)$ of the Cumulative Distribution Function (CDF) $F_{z}(\mu)={\rm Pr}(z\le\mu)$.

Discrete distributions are available in two sets of parameters:

• the Binomial distribution with the parameters $I$ and $p$   ⇒   $z \in \{0, 1, \text{...} \ , I \}$   ⇒   $M = I+1$ possible values,
• the Poisson distribution with the parameter $\lambda$   ⇒   $z \in \{0, 1, 2, 3, \text{...}\}$   ⇒   $M \to \infty$.

At the exercises below you are to compare:

• two Binomial distributions with different sets of parameters $I$ and $p$,
• two Poisson distributions with different rates $\lambda$,
• a Binomial distribution with a Poisson distribution.

Theoretical Background

Properties Of A Binomial Distribution

The Binomial distribution represents an important special case for the likelihood of occurence of a discrete random variable. For the derivation we assume, that $I$ binary and statistically independent random variables $b_i \in \{0, 1 \}$ can take

• the value $1$ with the probability ${\rm Pr}(b_i = 1) = p$, and
• the value $0$ with the probability ${\rm Pr}(b_i = 0) = 1-p$.

Then the sum $z$, which is also a discrete random variable with the symbol stock $\{0, 1, 2, \text{...}\ , I\}$, is called binomially distributed:

$$z=\sum_{i=1}^{I}b_i.$$

Der Symbolumfang beträgt somit $M = I + 1.$

Wahrscheinlichkeiten der Binomialverteilung

Hierfür gilt mit $μ = 0, \text{...}\ , I$:

$$p_\mu = {\rm Pr}(z=\mu)={I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$

Der erste Term gibt hierbei die Anzahl der Kombinationen $(I \text{ über }\mu)$ an:

$${I \choose \mu}=\frac{I !}{\mu !\cdot (I-\mu) !}=\frac{ {I\cdot (I- 1) \cdot \ \cdots \ \cdot (I-\mu+ 1)} }{ 1\cdot 2\cdot \ \cdots \ \cdot \mu}.$$

Momente der Binomialverteilung

Für das Moment $k$-ter Ordnung einer binomialverteilten Zufallsgröße gilt:

$$m_k={\rm E}[z^k]=\sum_{\mu={\rm 0}}^{I}\mu^k\cdot{I \choose \mu}\cdot p^\mu\cdot ({\rm 1}-p)^{I-\mu}.$$

Daraus erhält man nach einigen Umformungen für

• den linearen Mittelwert:   $m_1 = I\cdot p,$
• den quadratischen Mittelwert:   $m_2 = (I^2-I)\cdot p^2+I\cdot p,$
• die Varianz bzw. die Streuung:   $\sigma^2 = {m_2-m_1^2} = {I \cdot p\cdot (1-p)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \sigma = \sqrt{I \cdot p\cdot (1-p)}.$

Anwendungen der Binomialverteilung

Die Binomialverteilung findet in der Nachrichtentechnik ebenso wie in anderen Disziplinen mannigfaltige Anwendungen:

• Sie beschreibt die Verteilung von Ausschussstücken in der statistischen Qualitätskontrolle.
• Auch die per Simulation gewonnene Bitfehlerquote eines digitalen Übertragungssystems ist eigentlich eine binomialverteilte Zufallsgröße.
• Die Binomialverteilung erlaubt die Berechnung der Restfehlerwahrscheinlichkeit bei blockweiser Codierung, wie das folgende Beispiel zeigt.

$\text{Beispiel 1:}$  Überträgt man jeweils Blöcke von $I =5$ Binärsymbolen über einen Kanal, der

• mit der Wahrscheinlichkeit $p = 0.1$ ein Symbol verfälscht   ⇒   Zufallsgröße $e_i = 1$, und
• entsprechend mit der Wahrscheinlichkeit $1 - p = 0.9$ das Symbol unverfälscht überträgt   ⇒   Zufallsgröße $e_i = 0$,

so gilt für die neue Zufallsgröße $f$ („Fehler pro Block”):

$$f=\sum_{i=1}^{I}e_i.$$

Die Zufallsgröße $f$ kann nun alle ganzzahligen Werte zwischen $\mu = 0$ (kein Symbol verfälscht) und $\mu = I$ (alle fünf Symbole falsch) annehmen. Die Wahrscheinlichkeiten für $\mu$ Verfälschungen bezeichnen wir mit $p_μ = {\rm Pr}(f = \mu)$.

• Der Fall, dass alle fünf Symbole richtig übertragen werden, tritt mit der Wahrscheinlichkeit $p_0 = 0.9^{5} ≈ 0.5905$ ein. Dies ergibt sich auch aus der Binomialformel für $μ = 0$ unter Berücksichtigung der Definition „10 über 0“ = 1.
• Ein einziger Symbolfehler $(f = 1)$ tritt mit der Wahrscheinlichkeit $p_1 = 5\cdot 0.1\cdot 0.9^4\approx 0.3281$ auf. Der erste Faktor berücksichtigt, dass es für die Position eines einzigen Fehlers genau $5\text{ über } 1 = 5$ Möglichkeiten gibt. Die beiden weiteren Faktoren beücksichtigen, dass ein Symbol verfälscht und vier richtig übertragen werden müssen, wenn $f =1$ gelten soll.
• Für $f =2$ gibt es mehr Kombinationen, nämlich$5\text{ über } 2 = (5 \cdot 4)/(1 \cdot 2) = 10$, und man erhält $p_2 = 10\cdot 0.1^2\cdot 0.9^3\approx 0.0729$.

Kann ein Blockcode bis zu zwei Fehlern korrigieren, so ist die Restfehlerwahrscheinlichkeit $p_{\rm R} = 1-p_{\rm 0}-p_{\rm 1}-p_{\rm 2}\approx 0.85\%$. Eine zweite Berechnungsmöglichkeit wäre $p_{\rm R} = p_{3} + p_{4} + p_{5}$ mit der Näherung $p_{\rm R} \approx p_{3} = 0.81\%.$

Die mittlere Fehleranzahl in einem Block ist $m_f = 5 \cdot 0.1 = 0.5$. Die Varianz der Zufallsgröße $f$ beträgt $\sigma_f^2 = 5 \cdot 0.1 \cdot 0.9= 0.45$   ⇒   $\sigma_f \approx 0.671.$

Eigenschaften der Poissonverteilung

Die Poissonverteilung ist ein Grenzfall der Binomialverteilung, wobei

• zum einen von den Grenzübergängen $I → ∞$ und $p →$ 0 ausgegangen wird,
• zusätzlich vorausgesetzt ist, dass das Produkt $I · p = λ$ einen endlichen Wert besitzt.

Der Parameter $λ$ gibt die mittlere Anzahl der „Einsen” in einer festgelegten Zeiteinheit an und wird als die Rate bezeichnet.

Im Gegensatz zur Binomialverteilung ($0 ≤ μ ≤ I$) kann hier die Zufallsgröße beliebig große (ganzzahlige, nichtnegative) Werte annehmen, was bedeutet, dass die Menge der möglichen Werte hier nicht abzählbar ist. Da jedoch keine Zwischenwerte auftreten können, spricht man auch hier von einer diskreten Verteilung.

Wahrscheinlichkeiten der Poissonverteilung

Berücksichtigt man die oben genannten Grenzübergänge in der Gleichung für die Wahrscheinlichkeiten der Binomialverteilung, so folgt für die Auftrittswahrscheinlichkeiten der poissonverteilten Zufallsgröße $z$:

$$p_\mu = {\rm Pr} ( z=\mu ) = \lim_{I\to\infty} \cdot \frac{I !}{\mu ! \cdot (I-\mu )!} \cdot (\frac{\lambda}{I} )^\mu \cdot ( 1-\frac{\lambda}{I})^{I-\mu}.$$

Daraus erhält man nach einigen algebraischen Umformungen:

$$p_\mu = \frac{ \lambda^\mu}{\mu!}\cdot {\rm e}^{-\lambda}.$$

Momente der Poissonverteilung

Bei der Poissonverteilung ergeben sich Mittelwert und Streuung direkt aus den entsprechenden Gleichungen der Binomialverteilung durch zweifache Grenzwertbildung:

$$m_1 =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} I \cdot p= \lambda,$$

$$\sigma =\lim_{\left.{I\hspace{0.05cm}\to\hspace{0.05cm}\infty \atop {p\hspace{0.05cm}\to\hspace{0.05cm} 0}}\right.} \sqrt{I \cdot p \cdot (1-p)} = \sqrt {\lambda}.$$

Daraus ist zu erkennen, dass bei der Poissonverteilung stets $\sigma^2 = m_1 = \lambda$ ist. Dagegen gilt bei der Binomialverteilung immer $\sigma^2 < m_1$.

Momente der Poissonverteilung

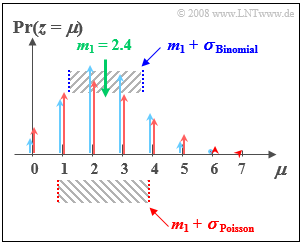
$\text{Beispiel 2:}$  Wir vergleichen nun

• die Binomialverteilung mit den Parametern $I =6$ und $p = 0.4$, und
• die Poissonverteilung mit $λ = 2.4$:
• Beide Verteilungen besitzen genau den gleichen Mittelwert $m_1 = 2.4$.
• Bei der Poissonverteilung (im Bild rot markiert) beträgt die Streuung $σ ≈ 1.55$.
• Bei der (blauen) Binomialverteilung ist die Standardabweichung nur $σ = 1.2$.

Anwendungen der Poissonverteilung

Die Poissonverteilung ist das Ergebnis eines so genannten Poissonprozesses. Ein solcher dient häufig als Modell für Folgen von Ereignissen, die zu zufälligen Zeitpunkten eintreten können. Beispiele für derartige Ereignisse sind

• der Ausfall von Geräten – eine wichtige Aufgabenstellung in der Zuverlässigkeitstheorie,
• das Schrotrauschen bei der optischen Übertragung, und
• der Beginn von Telefongesprächen in einer Vermittlungsstelle („Verkehrstheorie”).

$\text{Beispiel 3:}$  Gehen bei einer Vermittlungsstelle im Langzeitmittel neunzig Vermittlungswünsche pro Minute (entsprechend $λ = 1.5 \text{ pro Sekunde}$) ein, so lauten die Wahrscheinlichkeiten $p_µ$, dass in einem beliebigen Zeitraum von einer Sekunde genau $\mu$ Belegungen auftreten:

$$p_\mu = \frac{1.5^\mu}{\mu!}\cdot {\rm e}^{-1.5}.$$

Es ergeben sich die Zahlenwerte $p_0 = 0.223$, $p_1 = 0.335$, $p_2 = 0.251$, usw.

Daraus lassen sich weitere Kenngrößen ableiten:

• Die Abstand $τ$ zwischen zwei Vermittlungswünschen genügt der Exponentialverteilung.
• Die mittlere Zeitspanne zwischen Vermittlungswünschen beträgt ${\rm E}[τ] = 1/λ ≈ 0.667 \ \rm s$.

Gegenüberstellung Binomialverteilung vs. Poissonverteilung

Hier sollen die Gemeinsamkeiten und die Unterschiede zwischen binomial- und poissonverteilten Zufallsgrößen herausgearbeitet werden.

Binomialverteilung vs. Poissonverteilung

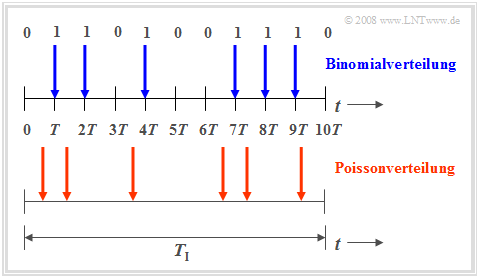
Die Binomialverteilung ist zur Beschreibung solcher stochastischer Ereignisse geeignet, die durch einen festen Takt $T$ gekennzeichnet sind. Beispielsweise beträgt bei ISDN (Integrated Services Digital Network) mit $64 \ \rm kbit/s$ die Taktzeit $T \approx 15.6 \ \rm µ s$.

• Nur in diesem Zeitraster treten binäre Ereignisse auf. Solche Ereignisse sind beispielsweise die fehlerfreie $(e_i = 0)$ oder fehlerhafte $(e_i = 1)$ Übertragung einzelner Symbole.
• Die Binomialverteilung ermöglicht nun statistische Aussagen über die Anzahl der in einem längeren Zeitintervall $T_{\rm I} = I · T$ zu erwartenden Übertragungsfehler entsprechend des oberen Zeitdiagramms (blau markierte Zeitpunkte).
• Für sehr große Werte von $I$ kann die Binomialverteilung durch die Poissonverteilung angenähert werden.
• Ist gleichzeitig das Produkt $I · p \gg 1$, so geht nach dem Grenzwertsatz von de Moivre-Laplace die Poissonverteilung (und damit auch die Binomialverteilung) in eine diskrete Gaußverteilung über.

Die Poissonverteilung macht ebenfallsAussagen über die Anzahl eintretender Binärereignisse in einem endlichen Zeitintervall.

Geht man hierbei vom gleichen Betrachtungszeitraum $T_{\rm I}$ aus und vergrößert die Anzahl $I$ der Teilintervalle immer mehr, so wird die Taktzeit $T$, zu der jeweils ein neues Binärereignis ($0$ oder $1$) eintreten kann, immer kleiner. Im Grenzfall geht $T$ gegen Null. Das heißt:

• Bei der Poissonverteilung sind die binären Ereignisse nicht nur zu diskreten, durch ein Zeitraster vorgegebenen Zeitpunkten möglich, sondern jederzeit. Das untere Zeitdiagramm verdeutlicht diesen Sachverhalt.
• Um im Mittel während der Zeit $T_{\rm I}$ genau so viele „Einsen” wie bei der Binomialverteilung zu erhalten (im Beispiel: sechs), muss allerdings die auf das infinitesimal kleine Zeitintervall $T$ bezogene charakteristische Wahrscheinlichkeit $p = {\rm Pr}( e_i = 1)$ gegen Null tendieren.

Versuchsdurchführung

In der folgenden Beschreibung bedeutet

• Blau: Verteilungsfunktion 1 (im Applet blau markiert)

• Rot: Verteilungsfunktion 2 (im Applet rot markiert)

(1)  Setzen Sie Blau: Binomialverteilung $(I=5, \ p=0.4)$ und Rot: Binomialverteilung $(I=10, \ p=0.2)$.

Wie lauten die Wahrscheinlichkeiten ${\rm Pr}(z=0)$ und ${\rm Pr}(z=1)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Blau: }{\rm Pr}(z=0)=0.6^5=7.78\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.4 \cdot 0.6^4=25.92\%;$

$\hspace{1.85cm}\text{Rot: }{\rm Pr}(z=0)=0.8^10=10.74\%, \hspace{0.3cm}{\rm Pr}(z=1)=0.2 \cdot 0.8^9=26.84\%.$

(2)  Es gelten weiter die Einstellungen von (1). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(3 \le z \le 5)$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Es gilt }{\rm Pr}(3 \le z \le 5) = {\rm Pr}(z=3) + {\rm Pr}(z=4) + {\rm Pr}(z=5)\text{, oder } {\rm Pr}(3 \le z \le 5) = {\rm Pr}(z \le 5) - {\rm Pr}(z \le 2)$

$\hspace{1.85cm}\text{Blau: }{\rm Pr}(3 \le z \le 5) = 0.2304+ 0.0768 + 0.0102 =1 - 0.6826 = 0.3174;$

$\hspace{1.85cm}\text{Rot: }{\rm Pr}(3 \le z \le 5) = 0.2013 + 0.0881 + 0.0264 = 0.9936 - 0.6778 = 0.3158$

(3)  Es gelten weiter die Einstellungen von (1). Wie unterscheiden sich der Mittelwert $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2; $

$\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 \le \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$

(4)  Setzen Sie Blau: Binomialverteilung $(I=15, p=0.3)$ und Rot: Poissonverteilung $(\lambda=4.5)$.

Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\hspace{0.15cm}\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$;

$\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;

(5)  Es gelten die Einstellungen von (4). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(z \gt 10)$ und ${\rm Pr}(z \gt 15)$

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0$.

$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0\hspace{0.5cm}\text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \ge {\rm Pr}(z = 16) = \frac{\lambda^{16} }{16!}\approx 2 \cdot 10^{-22}$

(6)  Es gelten weiter die Einstellungen von (4). Mit welchen Parametern ergeben sich symmetrische Verteilungen um $m_1$?

$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomialverung mit }p = 0.5\text{: }p_\mu = {\rm Pr}(z = \mu)\text{ symmetrisch um } m_1 = I/2 = 7.5 \ ⇒ \ p_μ = p_{I–μ}\ ⇒ \ p_8 = p_7, \ p_9 = p_6, \text{usw.}$

$\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

• Die erste Version wurde 2003 von Ji Li im Rahmen ihrer Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
• 2018 wurde dieses Programm von Jimmy He im Rahmen seiner Bachelorarbeit (Betreuer: Tasnád Kernetzky – Mitarbeiter der Professur „Leitungsgebundene Übertragungstechnik„) auf „HTML5” umgesetzt und neu gestaltet.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Applet in neuem Tab öffnen