Folgerungen aus dem Zuordnungssatz

1. Lineare zeitinvariante Systeme
2. Beschreibung kausaler realisierbarer Systeme
3. Folgerungen aus dem Zuordnungssatz

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

# ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL #

In den beiden ersten Kapiteln wurden aus Darstellungsgründen meist Filterfunktionen mit reellwertigen Frequenzgängen betrachtet, so dass die dazugehörige Zeitfunktion symmetrisch zum Nullzeitpunkt ist. Die Impulsantwort eines realisierbaren Systems muss aber stets kausal sein, das heißt, es muss $h(t)$ für $t < 0$ identisch Null sein. Diese starke Asymmetrie der Zeitfunktion $h(t)$ bedeutet aber gleichzeitig, dass der Frequenzgang $H(f)$ eines realisierbaren Systems stets komplex ist, wobei zwischen dessen Realteil und Imaginärteil ein fester Zusammenhang besteht.

Dieses dritte Kapitel bringt eine zusammenfassende Darstellung der Beschreibung kausaler realisierbarer Systeme, die sich auch von den mathematischen Methoden her von den bei akausalen Systemen üblichen Verfahren unterscheiden. Im Einzelnen wird nachfolgend behandelt:

• die Hilbert–Transformation, die aussagt, wie Real– und Imaginärteil von $H(f)$ zusammenhängen,
• die Laplace–Transformation, die bei kausalem $h(t)$ eine weitere Spektralfunktion $H_{\rm L}(p)$ liefert,
• die Beschreibung realisierbarer Systeme durch das Pol–Nullstellen–Diagramm, sowie
• die Laplace–Rücktransformation unter Anwendung der Funktionentheorie (Residuensatz).

Zu diesem Kapitel empfehlen wir

• zur Vorbereitung das Lernvideo Rechnen mit komplexen Zahlen, sowie
• das Interaktionsmodul Kausale Systeme – Laplacetransformation - eine zusammenhängende Darstellung des Lehrstoffs.

Voraussetzungen für das gesamte Kapitel „Realisierbare Systeme”

In den beiden ersten Kapiteln wurden meist reelle Übertragungsfunktionen $H(f)$ betrachtet, bei denen demzufolge die zugehörige Impulsantwort $h(t)$ stets symmetrisch zum Bezugszeitpunkt $t = 0$ war. Solche Übertragungsfunktionen

• eignen sich, um grundlegende Zusammenhänge einfach zu erklären,
• sind aber leider aus Kausalitätsgründen nicht realisierbar.

Dies wird deutlich, wenn man sich die Definition der Impulsantwort betrachtet:

$\text{Definition:}$  Die Impulsantwort $h(t)$ ist gleich dem Ausgangssignal $y(t)$ des Systems, wenn am Eingang zum Zeitpunkt $t = 0$ ein unendlich kurzer Impuls mit unendlich großer Ampltude anliegt:   $x(t) = δ(t)$. Man bezeichnet einen solchen Impuls als Diracimpuls.

Es ist offensichtlich, dass keine Impulsantwort realisiert werden kann, für die $h(t < 0) ≠ 0$ gilt.

$\text{Definition:}$  Bei einem kausalen System ist die Impulsantwort $h(t)$ für alle Zeiten $t < 0$ identisch $0$.

Die einzige reelle Übertragungsfunktion, die der Kausalitätsbedingung „Ausgangssignal kann nicht vor Eingangssignal beginnen” genügt, lautet:

$$H(f) = 1 \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h(t) = \delta(t).$$

Alle anderen reellwertigen Übertragungsfunktionen $H(f)$ beschreiben akausale Systeme und sind somit durch ein (elektrisches) Schaltungsnetzwerk nicht zu realisieren.

$\text{In anderen Worten:}$  Außer der idealen Übertragungsfunktion $H(f) = 1$ ist jede realistische Übertragungsfunktion komplex.

Real– und Imaginärteil einer kausalen Übertragungsfunktion

Eine jede kausale Impulsantwort $h(t)$ kann als Summe eines geraden Anteils $h_{\rm g}(t)$ und eines ungeraden Anteils $h_{\rm u}(t)$ dargestellt werden, wobei gilt:

$$\begin{align*} h_{ {\rm g}}(t) & = {1}/{2}\cdot \left[ h(t) + h(-t) \right]\hspace{0.05cm},\\ h_{ {\rm u}}(t) & = {1}/{2}\cdot \left[ h(t) - h(-t) \right] = h_{ {\rm g}}(t) \cdot {\rm sign}(t)\hspace{0.05cm} .\end{align*}$$

Hierbei ist die sogenannte Signum–Funktion verwendet:

$${\rm sign}(t) = \left\{ \begin{array}{c} -1 \\ +1 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} { t < 0,} \\ { t > 0.} \\ \end{array}$$

Aufteilung der Impulsantwort in einen geraden und einen ungeraden Anteil

$\text{Beispiel 1:}$  Die Grafik zeigt diese Aufspaltung für eine kausale exponentiell abfallende Impulsantwort

$$h(t) = \left\{ \begin{array}{c} 0 \\ 0.5/T \\ 1/T \cdot {\rm e}^{-t/T} \end{array} \right.\quad \begin{array}{c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \end{array}\begin{array}{*{20}c} { t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$

eines Tiefpasses erster Ordnung entsprechend Aufgabe 1.3Z.

Man erkennt:

• Für positive Zeiten gilt $h_{\rm g}(t) = h_{\rm u}(t) = h(t)/2$.
• Für negative Zeiten unterscheiden sich $h_{\rm g}(t)$ und $h_{\rm u}(t)$ nur durch das Vorzeichen.
• Für alle Zeiten gilt $h(t) = h_{\rm g}(t) + h_{\rm u}(t)$, auch zum Zeitpunkt $t = 0$ (durch Kreise markiert).

Betrachten wir nun den gleichen Sachverhalt im Spektralbereich. Nach dem Zuordnungssatz gilt für die komplexe Übertragungsfunktion:

$$H(f) = {\rm Re} \left\{ H(f) \right \} + {\rm j} \cdot {\rm Im} \left\{ H(f) \right \} \hspace{0.05cm},\hspace{5cm}$$

$${\rm Re} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm g}}(t)\hspace{0.05cm},$$

$${\rm j} \cdot {\rm Im} \left\{ H(f) \right\} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\quad h_{ {\rm u}}(t)\hspace{0.05cm}.$$

Zunächst soll an einem weiteren Beispiel der Zusammenhang zwischen Real– und Imaginärteil des Frequenzgangs $H(f)$ herausgearbeitet werden.

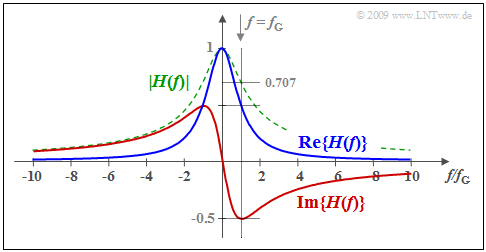
$\text{Beispiel 2:}$  Wir gehen von einem Tiefpass erster Ordnung aus, für dessen Übertragungsfunktion gilt:

$$H(f) = \frac{1}{1+{\rm j}\cdot f/f_{\rm G} } = \frac{1}{1+(f/f_{\rm G})^2}- {\rm j} \cdot \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2} \hspace{0.05cm}.$$

Hierbei gibt $f_{\rm G}$ die 3dB–Grenzfrequenz an, bei der $\vert H(f)\vert^2$ auf die Hälfte seines Maximums (bei $f = 0$) abgesunken ist. Die dazugehörige Impulsantwort $h(t)$ wurde bereits im Beispiel 1 dargestellt, wobei $f_{\rm G} = 1/(2πT)$ zu setzen ist.

Die Grafik zeigt den Realteil (blau) und den Imaginärteil (rot) von $H(f)$. Zusätzlich ist grün–gestrichelt der Betrag dargestellt.

Frequenzgang eines Tiefpasses erster Ordnung (Real– und Imaginärteil)

• Nachdem die beiden Zeitfunktionen $h_{\rm g}(t)$ und $h_{\rm u}(t)$ über die Signumfunktion zusammenhängen, sind auch Realteil ${\rm Re} \{H(f)\}$ und Imaginärteil ${\rm Im} \{H(f)\}$ fest miteinander verknüpft.
• Der Zusammenhang zwischen diesen Funktionen ist dabei durch die Hilbert–Transformation gegeben, die nachfolgend beschrieben wird.

Hilbert–Transformation

Wir betrachten hier ganz allgemein zwei Zeitfunktionen $u(t)$ und $w(t) = \sign(t) · u(t)$. Die dazugehörigen Spektralfunktionen werden mit $U(f)$ und ${\rm j} · W(f)$ bezeichnet. Das heißt, in diesem Abschnitt gilt ${w(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet {\rm j} \cdot W(f) }$ und nicht die sonst übliche Fourierkorrespondenz ${w(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet W(f)}.$

Mit der Fourierkorrespondenz   ${\rm sign}(t) \, \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \, {1}/({{\rm j} \, \pi f })$   erhält man nach Ausschreiben des Faltungsintegrals mit der Integrationsvariablen $ν$ :

$${\rm j} \cdot W(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, U(f) \quad \Rightarrow \quad W(f) = -\frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{U(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

Da aber gleichzeitig auch $u(t) = \sign(t) · w(t)$ zutrifft, gilt in gleicher Weise:

$$U(f) = \frac{1}{{\rm j} \, \pi f }\, \star \, {\rm j} \cdot W(f) \quad \Rightarrow \quad U(f) = \frac{1}{\pi }\int\limits_{-\infty}^{+\infty} { \frac{W(\nu)}{f - \nu}}\hspace{0.1cm}{\rm d}\nu \hspace{0.05cm}.$$

$\text{Definition:}$  Man benennt diese Integraltransformation nach ihrem Entdecker David Hilbert. Beide Varianten der Hilbert–Transformation werden im weiteren Verlauf mit folgenden Kurzzeichen gekennzeichnet:

$$W(f) \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad U(f) \hspace{0.8cm}{\rm bzw.}\hspace{0.8cm}W(f)= {\cal H}\left\{U(f) \right \}\hspace{0.05cm}.$$

• Zur Berechnung des durch die Pfeilspitze markierten Spektrums – hier $U(f)$ – wird von den beiden ansonsten identischen Gleichungen die zweite Gleichung (mit positivem Vorzeichen) genommen.
• Das durch den Kreis markierte Spektrum – hier $W(f)$ – ergibt sich dagegen aus der ersten Gleichung, also mit mit negativem Vorzeichen.

Bei doppelter Anwendung der Hilbert–Transformation erhält man wieder die ursprüngliche Funktion mit Vorzeichenwechsel, bei vierfacher Anwendung die ursprüngliche Funktion inklusive dem richtigen Vorzeichen:

$${\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} = -U(f), \hspace{0.2cm} {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ {\cal H}\left\{ U(f) \right \} \right \} \right \} \right \}= U(f)\hspace{0.05cm}.$$

$\text{Beispiel 3:}$  In [Mar94] findet man die folgende Hilbert–Korrespondenz:

$$\frac{1}{1+x^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{x}{1+x^2}\hspace{0.05cm}.$$

Hierbei steht $x$ stellvertretend für eine geeignet normierte Zeit– oder Frequenzvariable. Benutzen wir beispielsweise $x = f/f_{\rm G}$ als normierte Frequenzvariable, so erhält man daraus die Korrespondenz:

$$\frac{1}{1+(f/f_{\rm G})^2} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad \frac{f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$

Ausgehend von der Gleichung

$${\rm Im} \left\{ H(f) \right \} \quad \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow\quad {\rm Re} \left\{ H(f) \right \}$$

wird somit das auf der letzten Seite gefundene Ergebnis bestätigt:

$${\rm Im} \left\{ H(f) \right \} = \frac{-f/f_{\rm G} }{1+(f/f_{\rm G})^2}\hspace{0.05cm}.$$

Einige Paare von Hilbert–Korrespondenzen

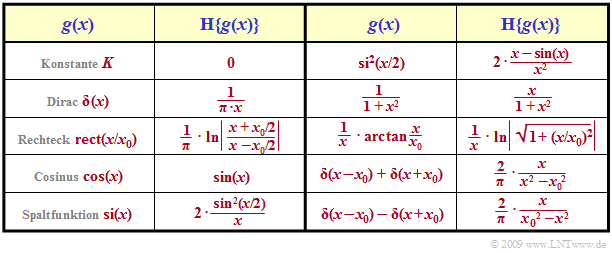
Zur Herleitung von Hilbert–Korrespondenzen geht man sehr pragmatisch vor, nämlich wie folgt:

• Man berechnet die Laplace–Transformierte $Y_{\rm L}(p)$ einer Zeitfunktion $y(t)$, wie im folgenden Abschnitt beschrieben. Diese ist somit bereits implizit kausal.
• Anschließend wandelt man die Spektralfunktion $Y_{\rm L}(p)$ in das zugehörige Fourierspektrum $Y(f)$ um und spaltet dieses in Real– und Imaginärteil auf. Dazu ersetzt man $p$ durch ${\rm j2}πf.$
• ${\rm Re} \{Y(f)\}$ und ${\rm Im} \{Y(f)\}$ sind somit ein Paar von Hilbert–Transformierten.
• Man ersetzt die Frequenzvariable $f$ durch $x$ sowie ${\rm Re} \{Y(f)\}$   ⇒   $g(x)$ bzw. ${\rm Im} \{Y(f)\}$   ⇒   ${\cal H} \{g(x)\}$.
• Die neue Variable $x$ kann sowohl eine geeignet normierte Frequenz oder auch eine normierte Zeit beschreiben. Somit ist die Hilbert–Transformation auf verschiedene Probleme anwendbar.

Tabelle mit Hilbert–Korrespondenzen

Die Tabelle zeigt einige solcher Hilbertpaare. Auf die Vorzeichen wurde verzichtet, so dass beide Richtungen gültig sind. Gilt beispielsweise ${\cal H} \{g(x)\} = f(x)$, so folgt daraus auch ${\cal H} \{f(x)\} = \, –g(x)$. Insbesondere gilt auch: $${\cal H}\left \{ \cos(x) \right\} = \sin(x)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\cal H}\left \{ \sin(x) \right\} = -\cos(x)\hspace{0.05cm}.$$

Dämpfung und Phase von Minimum–Phasen–Systemen

Eine wichtige Anwendung der Hilbert–Transformation stellt der Zusammenhang zwischen Dämpfung und Phase bei den sogenannten Minimum–Phasen–Systemen dar. Im Vorgriff auf das folgende Kapitel Laplace–Transformation und p–Übertragungsfunktion sei erwähnt, dass diese Systeme in der rechten $p$–Halbebene weder Pole noch Nullstellen aufweisen dürfen.

Allgemein gilt für die Übertragungsfunktion $H(f)$ mit dem komplexen Übertragungsmaß $g(f)$ sowie der Dämpfungsfunktion $a(f)$ und der Phasenfunktion $b(f)$: $$H(f) = {\rm e}^{-g(f)} = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} g(f) = a(f)+ {\rm j} \cdot b(f)\hspace{0.05cm}.$$ Bei den Minimum–Phasen–Systemen gilt nun aber nicht nur wie bei allen realisierbaren Systemen die Hilbert–Transformation bezüglich Imaginär– und Realteil  ⇒  ${\rm Im} \left\{ H(f) \right \} \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, {\rm Re} \left\{ H(f) \right \}\hspace{0.05cm},$ sondern zusätzlich auch noch die Hilbert–Korrespondenz zwischen Phasen– und Dämpfungsfunktion: $$b(f) \, \bullet\!\!-\!\!\!-\!\!\!-\!\!\hspace{-0.05cm}\rightarrow \, a(f)\hspace{0.05cm}.$$

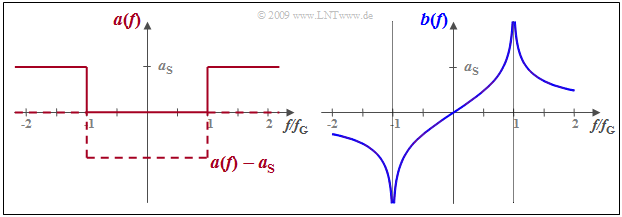
Ein Tiefpass besitze im Durchlassbereich, also für $|f| < f_{\rm G}$, den Frequenzgang $H(f) = 1$   ⇒   $a(f) =0 \ {\rm Np}$ , während für größere Frequenzen die Dämpfungsfunktion $a(f)$ den konstanten Wert $a_{\rm S}$ (in Neper) besitzt. In diesem Sperrbereich ist $H(f) = {\rm e}^{–a_{\rm S}}$ zwar sehr klein, aber nicht $0$.

Dämpfung und Phase eines beispielhaften Minimum–Phasen–Tiefpasses

Soll der Tiefpass kausal und damit realisierbar sein, so muss die Phasenfunktion $b(f)$ gleich der Hilbert–Transformierten der Dämpfung $a(f)$ sein. Da die Hilbert–Transformierte einer Konstanten $0$ ist, kann in gleicher Weise von der Funktion $a(f) - a_{\rm S}$ ausgegangen werden. Diese in der Grafik gestrichelt eingezeichnete Funktion ist zwischen $±f_{\rm G}$ (negativ) rechteckförmig. Entsprechend der Tabelle auf der letzten Seite gilt deshalb: $$b(f) = {a_{\rm S}}/{\pi} \cdot {\rm ln}\hspace{0.1cm}\left|\frac{f+f_{\rm G}}{f-f_{\rm G}}\right|\hspace{0.05cm}.$$ Jeder andere Phasenverlauf würde dagegen zu einer akausalen Impulsantwort führen.

Aufgaben zum Kapitel

Aufgabe 3.1: Kausalitätsbetrachtungen

Aufgabe 3.1Z: Hilbert-Transformierte