Verallgemeinerung auf N-dimensionale Zufallsgrößen

1. Stochastische Signaltheorie
2. Zufallsgrößen mit statistischen Bindungen
3. Verallgemeinerung auf N-dimensionale Zufallsgrößen

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Korrelationsmatrix

Bisher wurden nur statistische Bindungen zwischen zwei (skalaren) Zufallsgrößen betrachtet. Für den allgemeineren Fall einer Zufallsgröße mit $N$ Dimensionen bietet sich zweckmäßigerweise eine Vektor– bzw. Matrixdarstellung an. Für die folgende Beschreibung wird vorausgesetzt:

• Die $N$–dimensionale Zufallsgröße wird als Vektor dargestellt:

$${\mathbf{x}} = [\hspace{0.03cm}x_1, \hspace{0.03cm}x_2, \hspace{0.1cm}\text{...} \hspace{0.1cm}, \hspace{0.03cm}x_N]^{\rm T}.$$

Hierbei ist $\mathbf{x}$ ein Spaltenvektor, was aus dem Zusatz „T” – dies steht für „transponiert” – des angegebenen Zeilenvektors hervorgeht.

• Die $N$ Komponenten $x_i$ seien jeweils eindimensionale reelle Gaußsche Zufallsgrößen.

$\text{Definition:}$  Statistische Bindungen zwischen den $N$ Zufallsgrößen werden durch die Korrelationsmatrix vollständig beschrieben:

$${\mathbf{R} } =\left[ R_{ij} \right] = \left[ \begin{array}{cccc}R_{11} & R_{12} & \cdots & R_{1N} \\ R_{21} & R_{22}& \cdots & R_{2N} \\ \cdots & \cdots & \cdots &\cdots \\ R_{N1} & R_{N2} & \cdots & R_{NN} \end{array} \right] .$$

Die $N^2$ Elemente dieser $N×N$-Matrix geben jeweils das gemeinsame Moment erster Ordnung zwischen zwei Komponenten an:

$$R_{ij}= { {\rm E}[x_i \cdot x_j ] } = R_{ji} .$$

In Vektorschreibweise lautet somit die Korrelationsmatrix:

$$\mathbf{R}= {\rm E[\mathbf{x} \cdot {\mathbf{x} }^{\rm T} ] } .$$

Bitte beachten Sie:

• Da $\mathbf{x}$ ein Spaltenvektor mit $N$ Dimensionen ist und somit der transponierte Vektor $\mathbf{x}^{\rm T}$ ein Zeilenvektor gleicher Länge, ergibt das Produkt $\mathbf{x} · \mathbf{x}^{\rm T}$ eine $N×N$-Matrix.
• Dagegen wäre $\mathbf{x}^{\rm T}· \mathbf{x}$ eine $1×1$-Matrix, also ein Skalar. Für den hier nicht weiter betrachteten Sonderfall komplexer Komponenten $x_i$ sind auch die Matrixelemente komplex:

$$R_{ij}= {{\rm E}[x_i \cdot x_j^{\star} ]} = R_{ji}^{\star} .$$

• Die Realteile der Korrelationsmatrix ${\mathbf{R} }$ sind weiterhin symmetrisch zur Hauptdiagonalen, während sich die dazugehörigen Imaginärteile durch das Vorzeichen unterscheiden.

Kovarianzmatrix

$\text{Definition:}$  Man kommt von der Korrelationsmatrix $\mathbf{R} =\left[ R_{ij} \right]$ zur so genannten Kovarianzmatrix

$${\mathbf{K} } =\left[ K_{ij} \right] = \left[ \begin{array}{cccc} K_{11} & K_{12} & \cdots & K_{1N} \\ K_{21} & K_{22}& \cdots & K_{2N} \\ \cdots & \cdots & \cdots & \cdots \\ K_{N1} & K_{N2} & \cdots & K_{NN} \end{array} \right] ,$$

wenn die Matrixelemente $K_{ij} = {\rm E}[(x_i – m_i) · (x_j – m_j)]$ jeweils ein Zentralmoment erster Ordnung angeben.

Mit dem Vektor $\mathbf{m} = [m_1, m_2$, ... , $m_N]^{\rm T}$ kann somit auch geschrieben werden:

$$\mathbf{K}= { {\rm E}[(\mathbf{x} - \mathbf{m}) (\mathbf{x} - \mathbf{m})^{\rm T} ] } .$$

Es sei ausdrücklich darauf hingewiesen, dass $m_1$ den Mittelwert der Komponente $x_1$ und $m_2$ den Mittelwert von $x_2$ bezeichnet – nicht etwa das Moment erster bzw. zweiter Ordnung.

Die Kovarianzmatrix $\mathbf{K}$ zeigt bei reellen mittelwertfreien Gauß–Größen folgende weitere Eigenschaften:

• Das Element der $i$-ten Zeile und $j$-ten Spalte lautet mit den beiden Streuungen $σ_i$ und $σ_j$ und dem Korrelationskoeffizienten $ρ_{ij}$:

$$K_{ij} = σ_i · σ_j · ρ_{ij} = K_{ji}.$$

• Berücksichtigt man noch die Beziehung $ρ_{ii} = 1$, so erhält man für die Kovarianzmatrix:

$${\mathbf{K}} =\left[ K_{ij} \right] = \left[ \begin{array}{cccc} \sigma_{1}^2 & \sigma_{1}\sigma_{2}\rho_{12} & \cdots & \sigma_{1}\sigma_{N}\rho_{1N} \\ \sigma_{2}\sigma_{1}\rho_{21} & \sigma_{2}^2& \cdots & \sigma_{2}\sigma_{N}\rho_{2N} \\ \cdots & \cdots & \cdots & \cdots \\ \sigma_{N}\sigma_{1}\rho_{N1} & \sigma_{N}\sigma_{2}\rho_{N2} & \cdots & \sigma_{N}^2 \end{array} \right] .$$

• Aufgrund der Beziehung $ρ_{ij} = ρ_{ji}$ ist die Kovarianzmatrix bei reellen Größen stets symmetrisch zur Hauptdiagonalen. Bei komplexen Größen würde dagegen $ρ_{ij} = ρ_{ji}^{\star}$ gelten.

$\text{Beispiel 1:}$  Wir betrachten die drei Kovarianzmatrizen:

$${\mathbf{K}_2} = \left[ \begin{array}{cc} 1 & -0.5 \\ -0.5 & 1 \end{array} \right], \hspace{0.2cm}{\mathbf{K}_3} = 4 \cdot \left[ \begin{array}{ccc} 1 & 1/2 & 1/4\\ 1/2 & 1 & 3/4 \\ 1/4 & 3/4 & 1 \end{array}\right], \hspace{0.2cm}{\mathbf{K}_4} = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 9 & 0 \\ 0 & 0 & 0 & 16 \end{array} \right].$$

• $\mathbf{K}_2$ beschreibt eine 2D–Zufallsgröße, wobei der Korrelationskoeffizient $ρ$ zwischen den zwei Komponenten $-0.5$ beträgt und beide Komponenten die Streuung $σ = 1$ aufweisen.
• Bei der 3D-Zufallsgröße gemäß $\mathbf{K}_3$ haben alle Komponenten die gleiche Streuung $σ = 2$. Die stärksten Bindungen bestehen hier zwischen $x_2$ und $x_3$, wobei $ρ_{23} = 3/4$ gilt.
• Die vier Komponenten der durch $\mathbf{K}_4$ gekennzeichneten Zufallsgröße sind unkorreliert, bei Gaußscher WDF auch statistisch unabhängig. Die Varianzen sind $σ_i^2 = i^2$ für $i = 1$, ... , $4$   ⇒   Streuungen $σ_i = i$.

Zusammenhang zwischen Kovarianzmatrix und WDF

$\text{Definition:}$  Die Wahrscheinlichkeitsdichtefunktion (WDF) einer $N$-dimensionalen Gaußschen Zufallsgröße $\mathbf{x}$ lautet:

$$\mathbf{f_x}(\mathbf{x})= \frac{1}{\sqrt{(2 \pi)^N \cdot \vert\mathbf{K}\vert } }\cdot {\rm exp}{\left[-\frac{1}{2}\cdot(\mathbf{x} - \mathbf{m})^{\rm T}\cdot\mathbf{K}^{-1} \cdot(\mathbf{x} - \mathbf{m}) \right]} .$$

Hierbei bezeichnen:

• $\mathbf{x}$ den Spaltenvektor der betrachteten $N$-dimensionalen Zufallsgröße,
• $\mathbf{m}$ den Spaltenvektor der zugehörigen Mittelwerte,
• $\vert \mathbf{K}\vert$ die Determinante der $N×N$–Kovarianzmatrix $\mathbf{K}$ – eine skalare Größe,
• $\mathbf{K}^{−1}$ die Inverse von $\mathbf{K}$; diese ist ebenfalls eine $N×N$-Matrix.

Die Multiplikationen des Zeilenvektors $(\mathbf{x} – \mathbf{m})^{\rm T}$, der inversen Matrix $\mathbf{K}^{–1}$ und des Spaltenvektors $(\mathbf{x} – \mathbf{m})$ ergibt im Argument der Exponentialfunktion erwartungsgemäß ein Skalar.

$\text{Beispiel 2:}$  Wir betrachten wie im Beispiel 1 wieder eine 4D-Zufallsgröße $\mathbf{x}$, deren Kovarianzmatrix nur auf der Hauptdiagonalen besetzt ist:

$${\mathbf{K} } = \left[ \begin{array}{cccc} \sigma_{1}^2 & 0 & 0 & 0 \\ 0 & \sigma_{2}^2 & 0 & 0 \\ 0 & 0 & \sigma_{3}^2 & 0 \\ 0 & 0 & 0 & \sigma_{4}^2 \end{array} \right].$$

Deren Determinante ist $\vert \mathbf{K}\vert = σ_1^2 · σ_2^2 · σ_3^2 · σ_4^2$. Die inverse Kovarianzmatrix ergibt sich zu:

$${\mathbf{K} }^{-1} \cdot {\mathbf{K } } = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\mathbf{K} }^{-1} = \left[ \begin{array}{cccc} \sigma_{1}^{-2} & 0 & 0 & 0 \\ 0 & \sigma_{2}^{-2} & 0 & 0 \\ 0 & 0 & \sigma_{3}^{-2} & 0 \\ 0 & 0 & 0 & \sigma_{4}^{-2} \end{array} \right].$$

Für mittelwertfreie Größen $(\mathbf{m = 0})$ lautet somit die WDF:

$$\mathbf{f_{\rm x} }(\mathbf{x})= \frac{1}{ {(2 \pi)^2 \cdot \sigma_1\cdot \sigma_2\cdot \sigma_3\cdot \sigma_4} }\cdot {\rm exp}{\left[-(\frac{x_1^2}{2\sigma_1^2} \hspace{0.1cm}+\hspace{0.1cm}\frac{x_2^2}{2\sigma_2^2}\hspace{0.1cm}+\hspace{0.1cm}\frac{x_3^2}{2\sigma_3^2}\hspace{0.1cm}+\hspace{0.1cm}\frac{x_4^2}{2\sigma_4^2}) \right]} .$$

Ein Vergleich mit dem Kapitel Wahrscheinlichkeitsdichte- und Verteilungsfunktion zeigt, dass es sich um eine 4D-Zufallsgröße mit statistisch unabhängigen und unkorrelierten Komponenten handelt, da folgende Bedingung erfüllt ist:

$$\mathbf{f_x}(\mathbf{x})= \mathbf{f_{x1} }(\mathbf{x_1}) \cdot\mathbf{f_{x2} }(\mathbf{x_2}) \cdot\mathbf{f_{x3} }(\mathbf{x_3}) \cdot\mathbf{f_{x4} }(\mathbf{x_4}) .$$

Der Fall korrelierter Komponenten wird in den Aufgaben zu diesem Kapitel eingehend behandelt.

Die folgenden Links verweisen auf zwei Seiten am Kapitelende mit Grundlagen der Matrizenrechnung:

• Determinante einer Matrix
• Inverse einer Matrix

Eigenwerte und Eigenvektoren

Wir gehen weiter von einer $N×N$–Kovarianzmatrix $\mathbf{K}$ aus.

$\text{Definition:}$  Hieraus lassen sich die $N$ Eigenwerte $λ_1$, ... , $λ_N$ wie folgt berechnen:

$$\vert {\mathbf{K} } - \lambda \cdot {\mathbf{E} }\vert = 0.$$

$\mathbf{E}$ ist die Einheits-Diagonalmatrix der Dimension $N$.

$\text{Beispiel 3:}$  Ausgehend von einer 2×2-Matrix $\mathbf{K}$ mit $K_{11} = K_{22} = 1$ und $K_{12} = K_{21} = 0.8$ erhält man als Bestimmungsgleichung:

$${\rm det}\left[ \begin{array}{cc} 1- \lambda & 0.8 \\ 0.8 & 1- \lambda \end{array} \right] = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (1- \lambda)^2 - 0.64 = 0.$$

Die beiden Eigenwerte sind somit $λ_1 = 1.8$ und $λ_2 = 0.2$.

$\text{Definition:}$  Mit den so ermittelten Eigenwerten $λ_i (i = 1$, ... , $N)$ kann man die dazugehörigen Eigenvektoren $\boldsymbol{\xi_i}$ berechnen.
Die $N$ vektoriellen Bestimmungsgleichungen lauten dabei:

$$({\mathbf{K} } - \lambda_i \cdot {\mathbf{E} }) \cdot {\boldsymbol{\xi_i} } = 0\hspace{0.5cm}(i= 1, \hspace{0.1cm}\text{...} \hspace{0.1cm} , N).$$

$\text{Beispiel 4:}$  In Fortsetzung der Rechnung im Beispiel 3 ergeben sich die beiden folgenden Eigenvektoren:

$$\left[ \begin{array}{cc} 1- 1.8 & 0.8 \\ 0.8 & 1- 1.8 \end{array} \right]\cdot{\boldsymbol{\xi_1} } = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\boldsymbol{\xi_1} } = {\rm const.} \cdot\left[ \begin{array}{c} +1 \\ +1 \end{array} \right],$$

$$\left[ \begin{array}{cc} 1- 0.2 & 0.8 \\ 0.8 & 1- 0.2 \end{array} \right]\cdot{\boldsymbol{\xi_2} } = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\boldsymbol{\xi_2} } = {\rm const.} \cdot\left[ \begin{array}{c} -1 \\ +1 \end{array} \right].$$

Bringt man die Eigenvektoren in die so genannte Orthonormalfom (jeweils mit Betrag $1$), so lauten sie:

$${\boldsymbol{\xi_1} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} +1 \\ +1 \end{array} \right], \hspace{0.5cm}{\boldsymbol{\xi_2} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} -1 \\ +1 \end{array} \right].$$

Nutzung von Eigenwerten in der Informationstechnik

Zur Datenkompression mittels Eigenwertbestimmung

Abschließend soll diskutiert werden, wie Eigenwert und Eigenvektor in der Informationstechnik genutzt werden können, beispielsweise zum Zwecke der Datenreduktion.

Wir gehen von den Parameterwerten der Beispiele 3 und 4 aus.

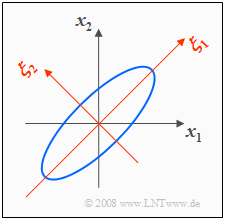
• Mit $σ_1 = σ_2 = 1$ und $ρ = 0.8$ ergibt sich die rechts skizzierte 2D-WDF mit elliptischen Höhenlinien.
• Die Ellipsenhauptachse liegt hier wegen $σ_1 = σ_2$ unter einem Winkel von $45^\circ$.

In der Grafik ist zusätzlich das $(ξ_1, ξ_2)$-Koordinatensystem eingezeichnet, das durch die Eigenvektoren $\mathbf{ξ}_1$ und $\mathbf{ξ}_2$ der Korrelationsmatrix aufgespannt wird:

• Die Eigenwerte $λ_1 = 1.8$ und $λ_2 = 0.2$ geben die Varianzen bezüglich des neuen Koordinatensystems an.
• Die Streuungen sind somit $σ_1 = \sqrt{1.8} ≈ 1.341$ und $σ_2 = \sqrt{0.2} ≈ 0.447$.

$\text{Beispiel 5:}$  Soll eine 2D-Zufallsgröße $\mathbf{x}$ in seinen beiden Dimensionen $x_1$ und $x_2$ im Bereich zwischen $–5σ$ und $+5σ$ im Abstand $Δx = 0.01$ quantisiert werden, so gibt es $\rm 10^6$ mögliche Quantisierungswerte $(σ_1 = σ_2 = σ = 1$ vorausgesetzt).

• Dagegen ist die Anzahl der möglichen Quantisierungswerte bei der gedrehten Zufallsgröße $\mathbf{ξ}$ um den Faktor $1.341 · 0.447 ≈ 0.6$ geringer.
• Das bedeutet: Allein durch die Drehung des Koordinatensystems um $45^\circ$ ⇒ Transformation der zweidimensionalen Zufallsgröße wurde eine Datenreduktion um $40\%$ erreicht.

Die Ausrichtung entsprechend den Hauptdiagonalen wurde für den zweidimensionalen Fall bereits auf der Seite Drehung des Koordinatensystems behandelt, und zwar basierend auf geometrischen und trigonometrischen Überlegungen.

Die Problemlösung mit Eigenwert und Eigenvektor ist äußerst elegant und problemlos auf beliebig große Dimensionen $N$ erweiterbar.

Grundlagen der Matrizenrechnung: Determinante einer Matrix

Wir betrachten die beiden quadratischen Matrizen mit Dimension $N = 2$ bzw. $N = 3$:

$${\mathbf{A}} = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right], \hspace{0.5cm}{\mathbf{B}} = \left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\right].$$

Die beiden Determinanten dieser Matrizen lauten:

$$|{\mathbf{A}}| = a_{11} a\cdot a_{22} - a_{12} \cdot a_{21},$$

$$|{\mathbf{B}}| = b_{11} \cdot b_{22} \cdot b_{33} + b_{12} \cdot b_{23} \cdot b_{31} + b_{13} \cdot b_{21} \cdot b_{32} - b_{11} \cdot b_{23} \cdot b_{32} - b_{12} \cdot b_{21} \cdot b_{33}- b_{13} \cdot b_{22} \cdot b_{31}.$$

Bitte beachten Sie:

• Die Determinante der Matrix $\mathbf{A}$ lässt sich geometrisch als die Fläche des durch die beiden Zeilenvektoren $(a_{11}, a_{12})$ und $(a_{21}, a_{22})$ aufgespannten Parallelogramms interpretieren.
• Die Fläche des durch die beiden Spaltenvektoren $(a_{11}, a_{21})^{\rm T}$ und $(a_{12}, a_{22})^{\rm T}$ festgelegten Parallelogramms ist ebenfalls $|\mathbf{A}|$.
• Dagegen ist die Determinante der Matrix $\mathbf{B}$ bei analoger geometrischer Interpretation als Volumen zu verstehen.

Für $N > 2$ ist es möglich, sogenannte Unterdeterminanten zu bilden. Die Unterdeterminante einer $N×N$–Matrix bezüglich der Stelle $i, j$ ist die Determinante der $(N–1)×(N–1)$–Matrix, die sich ergibt, wenn man die $i$-te Zeile und die $j$-te Spalte streicht. Als Kofaktor bezeichnet man dann den Wert der Unterdeterminante gewichtet mit dem Vorzeichen $(–1)^{i+j}$.

:  Ausgehend von der $3×3$–Matrix $\mathbf{B}$ lauten die Kofaktoren der zweiten Zeile:

$$B_{21} = -(b_{12} \cdot b_{23} - b_{13} \cdot b_{32})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j =3,$$

$$B_{22} = +(b_{11} \cdot b_{23} - b_{13} \cdot b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=4,$$

$$B_{23} = -(b_{11} \cdot b_{32} - b_{12} \cdot b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=5.$$

Die Determinante von $\mathbf{B}$ ergibt sich mit diesen Kofaktoren zu:

$$|{\mathbf{B}}| = b_{21} \cdot B_{21} +b_{22} \cdot B_{22} +b_{23} \cdot B_{23}.$$

Die Determinante wurde hier nach der zweiten Zeile entwickelt. Entwickelt man $\mathbf{B}$ nach einer anderen Zeile oder Spalte, so ergibt sich für $|\mathbf{B}|$ der gleiche Zahlenwert.

Grundlagen der Matrizenrechnung: Inverse einer Matrix

Häufig benötigt man die Inverse $\mathbf{M}^{–1}$ der quadratischen Matrix $\mathbf{M}$. Die inverse Matrix $\mathbf{M}^{–1}$ besitzt die gleiche Dimension $N$ wie $\mathbf{M}$ und ist wie folgt definiert, wobei $\mathbf{E}$ wieder die Einheitsmatrix (Diagonalmatrix) bezeichnet:

$${\mathbf{M}}^{-1} \cdot {\mathbf{M}} ={\mathbf{E}} = \left[ \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 1 \end{array} \right] .$$

Die Inverse der $2×2$–Matrix $\mathbf{A}$ lautet demnach:

$$\left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]^{-1} = \frac{1}{|{\mathbf{A}}|} \hspace{0.1cm}\cdot \left[ \begin{array}{cc} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{array} \right].$$

Hierbei gibt $|\mathbf{A}| = a_{11} · a_{22} – a_{12} · a_{21}$ die Determinante an. Entsprechend gilt für $N = 3$:

$$\left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\right]^{-1} = \frac{1}{|{\mathbf{B}}|} \hspace{0.1cm}\cdot\left[ \begin{array}{ccc} B_{11} & B_{21} & B_{31}\\ B_{12} & B_{22} & B_{32}\\ B_{13} & B_{23} & B_{33} \end{array}\right].$$

Die Determinante $|\mathbf{B}|$ einer $3×3$–Matrix wurde auf der letzten Seite angegeben, ebenso wie die Berechnungsvorschrift der Kofaktoren $B_{ij}$:

• Diese beschreiben die Unterdeterminanten von $\mathbf{B}$, gewichtet mit den Positionsvorzeichen $(–1)^{i+j}$.
• Zu beachten ist die Vertauschung der Zeilen und Spalten bei der Inversen.

Aufgaben zum Kapitel

Aufgabe 4.15: WDF und Korrelationsmatrix

Aufgabe 4.15Z: Aussagen der Kovarianzmatrix

Aufgabe 4.16: Eigenwerte und Eigenvektoren

Aufgabe 4.16Z: 2D- und 3D-Datenreduktion