Digitale Filter
Inhaltsverzeichnis
Allgemeines Blockschaltbild
Jedes Signal $x(t)$ kann an einem Rechner nur durch die Folge $〈x_ν〉$ seiner Abtastwerte dargestellt werden, wobei $x_ν$ für $x(ν · T_{\rm A})$ steht. Der zeitliche Abstand $T_{\rm A}$ zwischen zwei Abtastwerten ist dabei durch das Abtasttheorem nach oben begrenzt.
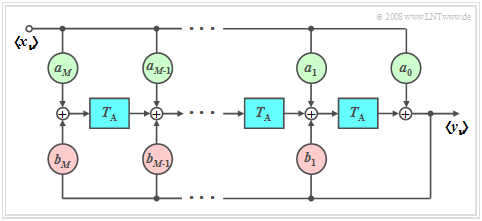
Um den Einfluss eines linearen Filters mit dem Frequenzgang $H(f)$ auf das zeitdiskrete Signal $〈x_ν〉$ zu erfassen, bietet es sich an, auch das Filter zeitdiskret zu beschreiben. Nachfolgend sehen Sie das entsprechende Blockschaltbild.
Für die Abtastwerte des Ausgangssignals gilt somit:
- $$y_\nu = \sum\limits_{\mu = 0}^M {a_\mu } \cdot x_{\nu - \mu } + \sum\limits_{\mu = 1}^M {b_\mu } \cdot y_{\nu - \mu } .$$
Hierzu ist folgendes zu bemerken:
- Die erste Summe beschreibt die Abhängigkeit des aktuellen Wertes $y_ν$ am Filterausgang vom aktuellen Eingangswert $x_ν$ und von den $M$ vorherigen Eingangswerten $x_{ν–1}$, ... , $x_{ν–M}.$
- Die zweite Summe kennzeichnet die Beeinflussung von $y_ν$ durch die vorherigen Werte $y_{ν–1}$, ... , $y_{ν–M}$ am Filterausgang. Sie gibt somit den rekursiven Teil des Filters an.
- Man bezeichnet den ganzzahligen Parameter $M$ als die Ordnung des digitalen Filters.
Nichtrekursives Filter
$\text{Definition:}$ Sind alle Rückführungskoeffizienten $b_{\mu} = 0$, so spricht von einem nichtrekursiven Filter.
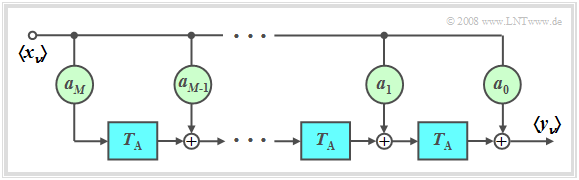
Ein solches nichtrekursives Filter $M$–ter Ordnung besitzt folgende Eigenschaften:
- Der Ausgangswert $y_ν$ hängt nur vom aktuellen und den $M$ vorherigen Eingangswerten ab:
- $$y_\nu = \sum\limits_{\mu = 0}^M {a_\mu \cdot x_{\mu - \nu } } .$$
- Die Filterimpulsantwort erhält man daraus mit $x(t) = δ(t)$ (das entsprechende Eingangssignal in zeitdiskreter Schreibweise ist $x_ν ≡0$ mit Ausnahme von $x_0 =1$):
- $$h(t) = \sum\limits_{\mu = 0}^M {a_\mu \cdot \delta ( {t - \mu \cdot T_{\rm A} } )} .$$
- Durch Anwendung des Verschiebungssatzes folgt daraus für den Filterfrequenzgang:
- $$H(f) = \sum\limits_{\mu = 0}^M {a_\mu \cdot {\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}f\mu T_{\rm A} } } .$$
$\text{Beispiel 1:}$ Ein Zweiwegekanal, bei dem
- das Signal auf dem Hauptpfad gegenüber dem Eingangssignal ungedämpft, aber um $2\ \rm µ s$ verzögert ankommt, und
- in $4\ \rm µ s$ Abstand – also absolut zur Zeit $t = 6\ \rm µ s$ – ein Echo mit halber Amplitude nachfolgt,
kann durch ein nichtrekursives Filter entsprechend obiger Skizze nachgebildet werden, wobei folgende Parameterwerte einzustellen sind:
- $$M = 3,\quad T_{\rm A} = 2\;{\rm{µ s} },\quad a_{\rm 0} = 0,\quad a_{\rm 1} = 1, \quad a_{\rm 2} = 0, \quad a_{\rm 3} = 0.5.$$
Rekursives Filter
$\text{Definition:}$ Sind alle Vorwärtskoeffizienten mit Ausnahme von $a_0$ identisch $a_\nu = 0$, so liegt ein (rein) rekursives Filter vor.
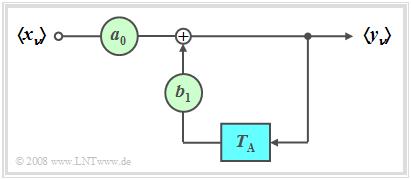
Im Folgenden beschränken wir uns auf den Sonderfall $M = 1$ (Blockschaltbild entsprechend Grafik):
Dieses Filter weist folgende Eigenschaften auf:
- Der Ausgangswert $y_ν$ hängt (indirekt) von unendlich vielen Eingangswerten ab, wie die folgende Rechung zeigt:
- $$y_\nu = a_0 \cdot x_\nu + b_1 \cdot y_{\nu - 1} = a_0 \cdot x_\nu + a_0 \cdot b_1 \cdot x_{\nu - 1} + {b_1} ^2 \cdot y_{\nu - 2} $$
- $$\Rightarrow \hspace{0.3cm} y_\nu = \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot x_{\nu - \mu } .}$$
- Die zeitdiskrete Impulsantwort $〈h_\mu〉$ ist definitionsgemäß der Ausgangsfolge, wenn am Eingang eine einzelne „Eins” bei $t =0$ anliegt.
- Die (zeitdiskrete) Impulsantwort eines rekursiven Filters reicht schon mit $M = 1$ bis ins Unendliche:
- $$h(t)= \sum\limits_{\mu = 0}^\infty {a_0 \cdot {b_1} ^\mu \cdot \delta ( {t - \mu \cdot T_{\rm A} } )}$$
- $$\Rightarrow 〈h_\mu〉= 〈a_0, \ a_0\cdot {b_1}, \ a_0\cdot {b_1}^2 \ \text{...} 〉.$$
- Aus Stabilitätsgründen muss $b_1 < 1$ gelten. Bei $b_1 = 1$ würde sich die Impulsantwort $h(t)$ bis ins Unendliche erstrecken und bei $b_1 > 1$ würde $h(t)$ sogar bis ins Unendliche anklingen.
- Bei einem solchen rekursiven Filter erster Ordnung ist jede einzelne Diraclinie genau um den Faktor $b_1$ kleiner als die vorherige Diraclinie:
- $$h_{\mu} = h(\mu \cdot T_{\rm A}) = {b_1} \cdot h_{\mu -1}.$$
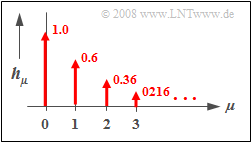
$\text{Beispiel 2:}$ Die nebenstehende Grafik zeigt die zeitdiskrete Impulsantwort $〈h_\mu〉$ eines rekursiven Filters erster Ordnung mit den Parametern $a_0 = 1$ und $b_1 = 0.6$.
- Der Verlauf ist exponentiell abfallend und erstreckt sich bis ins Unendliche.
- Das Verhältnis der Gewichte zweier aufeinander folgender Diracs ist jeweils $b_1 = 0.6$.
Aufgaben zum Kapitel
Aufgabe 5.3: Digitales Filter 1. Ordnung
Aufgabe 5.3Z: Nichtrekursives Filter