Gedächtnislose Nachrichtenquellen
Inhaltsverzeichnis
# ÜBERBLICK ZUM ERSTEN HAUPTKAPITEL #
Dieses erste Kapitel beschreibt die Berechnung und die Bedeutung der Entropie. Diese ist entsprechend der Shannonshen Informationsdefinition ein Maß für die mittlere Unsicherheit über den Ausgang eines statistischen Ereignisses oder die Unsicherheit bei der Messung einer stochastischen Größe. Etwas salopp ausgedrückt quantifiziert die Entropie einer Zufallsgröße deren „Zufälligkeit”.
Im Einzelnen werden behandelt:
- der Entscheidungsgehalt und die Entropie einer gedächtnislosen Nachrichtenquelle,
- die binäre Entropiefunktion und deren Anwendung auf nichtbinäre Quellen,
- die Entropieberechnung bei gedächtnisbehafteten Quellen und geeignete Näherungen,
- die Besonderheiten von Markovquellen hinsichtlich der Entropieberechnung,
- die Vorgehensweise bei Quellen mit großem Symbolumfang, zum Beispiel natürliche Texte,
- die Entropieabschätzungen nach Shannon und Küpfmüller.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Versuch „Wertdiskrete Informationstheorie” des Praktikums „Simulation Digitaler Übertragungssysteme ”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Windows-Programm WDIT ⇒ Link verweist auf die ZIP-Version des Programms; und
- der zugehörigen Praktikumsanleitung ⇒ Link verweist auf die PDF-Version.
Modell und Voraussetzungen
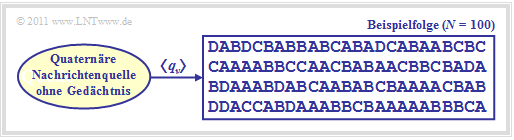
Wir betrachten eine wertdiskrete Nachrichtenquelle $\rm Q$, die eine Folge $ \langle q_ν \rangle$ von Symbolen abgibt.
- Für die Laufvariable gilt $ν = 1$, ... , $N$, wobei $N$ „hinreichend groß” sein sollte.
- Jedes einzelne Quellensymbol $q_ν$ entstammt einem Symbolvorrat $\{q_μ \}$ mit $μ = 1$, ... , $M$, wobei $M$ den Symbolumfang bezeichnet:
- $$q_{\nu} \in \left \{ q_{\mu} \right \}, \hspace{0.15cm}{\rm mit}\hspace{0.15cm} \nu = 1, \hspace{0.05cm} \text{ ...}\hspace{0.05cm} , N\hspace{0.15cm}{\rm und}\hspace{0.15cm}\mu = 1,\hspace{0.05cm} \text{ ...}\hspace{0.05cm} , M \hspace{0.05cm}.$$
Die Grafik zeigt eine quaternäre Nachrichtenquelle $(M = 4)$ mit dem Alphabet $\rm \{A, B, C, D\}$ und eine beispielhafte Folge der Länge $N = 100$.
Es gelten folgende Voraussetzungen:
- Die quaternäre Nachrichtenquelle wird durch $M = 4$ Symbolwahrscheinlichkeiten $p_μ$ vollständig beschrieben. Allgemein gilt:
- $$\sum_{\mu = 1}^M \hspace{0.1cm}p_{\mu} = 1 \hspace{0.05cm}.$$
- Die Nachrichtenquelle sei gedächtnislos, das heißt, die einzelnen Folgenelemente seien statistisch voneinander unabhängig:
- $${\rm Pr} \left (q_{\nu} = q_{\mu} \right ) = {\rm Pr} \left (q_{\nu} = q_{\mu} \hspace{0.03cm} | \hspace{0.03cm} q_{\nu -1}, q_{\nu -2}, \hspace{0.05cm} \text{ ...}\hspace{0.05cm}\right ) \hspace{0.05cm}.$$
- Da das Alphabet aus Symbolen (und nicht aus Zufallsgrößen) besteht, ist hier die Angabe von Erwartungswerten (linearer Mittelwert, quadratischer Mittelwert, Streuung, usw.) nicht möglich, aus informationstheoretischer Sicht aber auch nicht nötig.
Diese Eigenschaften werden nun mit einem Beispiel verdeutlicht.
$\text{Beispiel 1:}$ Für die Symbolwahrscheinlichkeiten einer Quaternärquelle gelte:
- $$p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}.$$
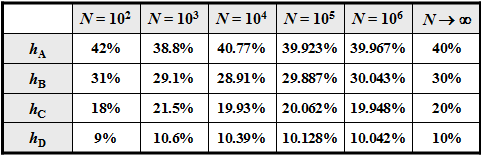
Bei einer unendlich langen Folge $(N \to \infty)$ wären die relativen Häufigkeiten $h_{\rm A}$, $h_{\rm B}$, $h_{\rm C}$ und $h_{\rm D}$ – also die a–posteriori–Kenngrößen – identisch mit den a–priori–Wahrscheinlichkeiten $p_{\rm A}$, $p_{\rm B}$, $p_{\rm C}$ und $p_{\rm D}$.
Bei kleinerem $N$ kann es aber durchaus zu Abweichungen kommen, wie die nebenstehende Tabelle (Ergebnis einer Simulation) zeigt. Eine beispielhafte Folge mit $N = 100$ Symbolen ist ist in der oberen Grafik angegeben.
Aufgrund der Mengenelemente $\rm A$, $\rm B$, $\rm C$ und $\rm D$ können keine Mittelwerte angegeben werden. Ersetzt man die Symbole durch Zahlenwerte, zum Beispiel $\rm A \Rightarrow 1$, $\rm B \Rightarrow 2$, $\rm C \Rightarrow 3$, $\rm D \Rightarrow 4$, so ergeben sich
- für den linearen Mittelwert:
- $$m_1 = {\rm E} \left [ q_{\nu} \right ] = {\rm E} \left [ q_{\mu} \right ] = 0.4 \cdot 1 + 0.3 \cdot 2 + 0.2 \cdot 3 + 0.1 \cdot 4 = 2 \hspace{0.05cm},$$
- für den quadratischen Mittelwert:
- $$m_2 = {\rm E} \left [ q_{\nu}^{\hspace{0.05cm}2} \right ] = {\rm E} \left [ q_{\mu}^{\hspace{0.05cm}2} \right ] = 0.4 \cdot 1^2 + 0.3 \cdot 2^2 + 0.2 \cdot 3^2 + 0.1 \cdot 4^2 = 5 \hspace{0.05cm},$$
- für die Standardabweichung (Streuung) nach dem „Satz von Steiner”:
- $$\sigma = \sqrt {m_2 - m_1^2} = \sqrt {5 - 2^2} = 1 \hspace{0.05cm}.$$
Entscheidungsgehalt – Nachrichtengehalt
Claude Elwood Shannon definierte 1948 im Standardwerk der Informationstheorie [Sha48][1] den Informationsbegriff als „Abnahme der Ungewissheit über das Eintreten eines statistischen Ereignisses”.
Machen wir hierzu ein gedankliches Experiment mit $M$ möglichen Ergebnissen, die alle gleichwahrscheinlich seien: $p_1 = p_2 = \hspace{0.05cm} \text{ ...}\hspace{0.05cm} = p_M = 1/M \hspace{0.05cm}.$
Unter dieser Annahme gilt:
- Ist $M = 1$, so wird jeder einzelne Versuch das gleiche Ergebnis liefern und demzufolge besteht keine Unsicherheit hinsichtlich des Ausgangs. Wird uns das Versuchsergebnis mitgeteilt, so haben wir dadurch natürlich auch keinen Informationsgewinn.
- Dagegen erfährt ein Beobachter bei einem Experiment mit $M = 2$, zum Beispiel dem „Münzwurf” mit der Ereignismenge $\{\rm \boldsymbol{\rm Z}(ahl), rm \boldsymbol{\rm W}(app) \}$ und den Wahrscheinlichkeiten $p_{\rm Z}$ = $p_{\rm W} = 0.5$, durchaus einen Informationsgewinn. Die Unsicherheit hinsichtlich $\rm Z$ bzw. $\rm W$ wird aufgelöst.
- Beim Experiment „Würfeln” $(M = 6)$ und noch mehr beim Roulette $(M = 37)$ ist die gewonnene Information für den Beobachter noch deutlich größer als beim „Münzwurf”, wenn er erfährt, welche Zahl gewürfelt bzw. welche Kugel gefallen ist.
- Schließlich sollte noch berücksichtigt werden, dass das Experiment „Dreifacher Münzwurf” mit den $M = 8$ möglichen Ergebnissen $\rm ZZZ$, $\rm ZZW$, $\rm ZWZ$, $\rm ZWW$, $\rm WZZ$, $\rm WZW$, $\rm WWZ$, $\rm WWW$ die dreifache Information liefert wie der einfache Münzwurf $(M = 2)$.
Die nachfolgende Festlegung erfüllt alle hier verbal aufgeführten Anforderungen an ein quantitatives Informationsmaß bei gleichwahrscheinlichen Ereignissen, gekennzeichnet durch den Symbolumfang $M$.
$\text{Definition:}$ Der Entscheidungsgehalt einer Nachrichtenquelle hängt nur vom Symbolumfang $M$ ab und ergibt sich zu
- $$H_0 = {\rm log}\hspace{0.1cm}M = {\rm log}_2\hspace{0.1cm}M \hspace{0.15cm}\text {(in "bit")} = {\rm ln}\hspace{0.1cm}M \hspace{0.15cm}\text {(in "nat")} = {\rm lg}\hspace{0.1cm}M \hspace{0.15cm}\text {(in "Hartley")}\hspace{0.05cm}.$$
Gebräuchlich ist hierfür auch die Bezeichnung Nachrichtengehalt. Da $H_0$ gleichzeitig den Maximalwert der Entropie $H$ angibt, wird in unserem Tutorial teilweise auch $H_\text{max}$ als Kurzzeichen verwendet.
Zu unserer Nomenklatur ist anzumerken:
- Der Logarithmus wird im Folgenden unabhängig von der Basis mit „log” bezeichnet. Die oben genannten Relationen werden aufgrund folgender Eigenschaften erfüllt:
- $${\rm log}\hspace{0.1cm}1 = 0 \hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}37 > {\rm log}\hspace{0.1cm}6 > {\rm log}\hspace{0.1cm}2\hspace{0.05cm},\hspace{0.2cm} {\rm log}\hspace{0.1cm}M^k = k \cdot {\rm log}\hspace{0.1cm}M \hspace{0.05cm}.$$
- Meist verwenden wir den Logarithmus zur Basis $2$ ⇒ Logarithmus dualis $\rm (ld)$, wobei dann die Pseudoeinheit „bit” – genauer: „bit/Symbol” – hinzugefügt wird:
- $${\rm ld}\hspace{0.1cm}M = {\rm log_2}\hspace{0.1cm}M = \frac{{\rm lg}\hspace{0.1cm}M}{{\rm lg}\hspace{0.1cm}2} = \frac{{\rm ln}\hspace{0.1cm}M}{{\rm ln}\hspace{0.1cm}2} \hspace{0.05cm}.$$
- Weiter findet man in der Literatur vereinzelt auch die oben zusätzlich angegebenen Definitionen, die auf dem natürlichen Logarithmus $\rm (ln)$ oder dem Zehnerlogarithmus $\rm (lg)$ basieren.
Informationsgehalt und Entropie
Wir verzichten nun auf die bisherige Voraussetzung, dass alle $M$ möglichen Ergebnisse eines Versuchs gleichwahrscheinlich seien. Im Hinblick auf eine möglichst kompakte Schreibweise legen wir für diese Seite lediglich fest:
- $$p_1 > p_2 > \hspace{0.05cm} \text{ ...}\hspace{0.05cm} > p_\mu > \hspace{0.05cm} \text{ ...}\hspace{0.05cm} > p_{M-1} > p_M\hspace{0.05cm},\hspace{0.4cm}\sum_{\mu = 1}^M p_{\mu} = 1 \hspace{0.05cm}.$$
Wir betrachten nun den Informationsgehalt der einzelnen Symbole, wobei wir den Logarithmus dualis mit $\log_2$ bezeichnen :
- $$I_\mu = {\rm log_2}\hspace{0.1cm}\frac{1}{p_\mu}= -\hspace{0.05cm}{\rm log_2}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
Man erkennt:
- Wegen $p_μ ≤ 1$ ist der Informationsgehalt nie negativ. Im Grenzfall $p_μ \to 1$ geht $I_μ \to 0$.
- Allerdings ist für $I_μ = 0$ ⇒ $p_μ = 1$ ⇒ $M = 1$ auch der Entscheidungsgehalt $H_0 = 0$.
- Bei abfallenden Wahrscheinlichkeiten $p_μ$ nimmt der Informationsgehalt kontinuierlich zu:
- $$I_1 < I_2 < \hspace{0.05cm} \text{ ...}\hspace{0.05cm} < I_\mu <\hspace{0.05cm} \text{ ...}\hspace{0.05cm} < I_{M-1} < I_M \hspace{0.05cm}.$$
$\text{Fazit:}$ Je unwahrscheinlicher ein Ereignis ist, desto größer ist sein Informationsgehalt. Diesen Sachverhalt stellt man auch im täglichen Leben fest:
- „6 Richtige” im Lotto nimmt man sicher eher wahr als „3 Richtige” oder gar keinen Gewinn.
- Ein Tsunami in Asien dominiert auch die Nachrichten in Deutschland über Wochen im Gegensatz zu den fast standardmäßigen Verspätungen der Deutschen Bahn.
- Eine Niederlagenserie von Bayern München führt zu Riesen–Schlagzeilen im Gegensatz zu einer Siegesserie. Bei 1860 München ist genau das Gegenteil der Fall.
Der Informationsgehalt eines einzelnen Symbols (oder Ereignisses) ist allerdings nicht sehr interessant. Dagegen erhält man eine der zentralen Größen der Informationstheorie
- durch Scharmittelung über alle möglichen Symbole $q_μ$ bzw.
- durch Zeitmittelung über alle Elemente der Folge $\langle q_ν \rangle$.
$\text{Definition:}$ Die Entropie $H$ einer Quelle gibt den mittleren Informationsgehalt aller Symbole an:
- $$H = \overline{I_\nu} = {\rm E}\hspace{0.01cm}[I_\mu] = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{p_\mu}= -\sum_{\mu = 1}^M p_{\mu} \cdot{\rm log_2}\hspace{0.1cm}{p_\mu} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit[/Symbol])} \hspace{0.05cm}.$$
Die überstreichende Linie kennzeichnet eine Zeitmittelung und $\rm E[\text{...}]$ eine Scharmittelung.
Die Entropie ist ein Maß für
- die mittlere Unsicherheit über den Ausgang eines statistischen Ereignisses,
- die „Zufälligkeit” dieses Ereignisses,
- den mittleren Informationsgehalt einer Zufallsgröße.
Binäre Entropiefunktion
Wir beschränken uns zunächst auf den Sonderfall $M = 2$ und betrachten eine binäre Quelle, die die beiden Symbole $\rm A$und $\rm B$ abgibt. Die Auftrittwahrscheinlichkeiten seien $p_{\rm A} = p$ und $p_{\rm B} = 1 – p$.
Für die Entropie dieser Binärquelle gilt:
- $$H_{\rm bin} (p) = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + (1-p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1-p} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
Man nennt diese Funktion $H_\text{bin}(p)$ die binäre Entropiefunktion. Die Entropie einer Quelle mit größerem Symbolumfang $M$ lässt sich häufig unter Verwendung von $H_\text{bin}(p)$ ausdrücken.
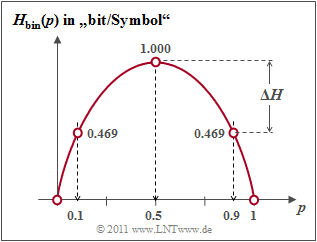
Die Grafik zeigt die Funktion $H_\text{bin}(p)$ für die Werte $0 ≤ p ≤ 1$ der Symbolwahrscheinlichkeit von $\rm A$ (oder auch von $\rm B$). Man erkennt:
- Der Maximalwert $H_\text{max} = 1\; \rm bit$ ergibt sich für $p = 0.5$, also für gleichwahrscheinliche Binärsymbole. Dann liefern $\rm A$ und $\rm B$ jeweils den gleichen Beitrag zur Entropie.
- $H_\text{bin}(p)$ ist symmetrisch um $p = 0.5$. Eine Quelle mit $p_{\rm A} = 0.1$ und $p_{\rm B} = 0.9$ hat die gleiche Entropie (Zufälligkeit) $H = 0.469 \; \rm bit$ wie eine Quelle mit $p_{\rm A} = 0.9$ und $p_{\rm B} = 0.1$.
- Die Differenz $ΔH$ = $H_\text{max} - H$ gibt die Redundanz der Quelle an und $r = ΔH/H_\text{max}$ die relative Redundanz. Im Beispiel ergeben sich $ΔH = 0.531\; \rm bit$ bzw. $r = 53.1\; \rm \%$.
- Für $p = 0$ ergibt sich $H = 0$, da hier die Symbolfolge $\rm B \ B \ B \text{...}$ mit Sicherheit vorhergesagt werden kann. Eigentlich ist nun der Symbolumfang nur noch $M = 1$. Gleiches gilt für $p = 1$, also für die Symbolfolge $\rm A \ A A \text{...}$ .
- Die binäre Entropiefunktion ist stets konkav, da deren zweite Ableitung nach dem Parameter $p$ für alle Werte von $p$ negativ ist:
- $$\frac{{\rm d}^2H_{\rm bin} (p)}{{\rm d}\,p^2} = \frac{-1}{{\rm ln}(2) \cdot p \cdot (1-p)}< 0 \hspace{0.05cm}.$$
Nachrichtenquellen mit größerem Symbolumfang
Im ersten Abschnitt dieses Kapitels haben wir eine quaternäre Nachrichtenquelle $(M = 4)$ mit den Symbolwahrscheinlichkeiten $p_{\rm A} = 0.4 \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = 0.3 \hspace{0.05cm},\hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm},\hspace{0.2cm} p_{\rm D} = 0.1\hspace{0.05cm}$ betrachtet. Diese besitzt die folgende Entropie:
- $$\begin{align*}H_{\rm quat} \hspace{-0.1cm} & = \hspace{-0.1cm} 0.4 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.3} + 0.2 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.2}+ 0.1 \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.1}=\\ \hspace{-0.1cm} & = \hspace{-0.1cm}\frac{1}{{\rm lg}\hspace{0.1cm}2} \cdot \left [ 0.4 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.4} + 0.3 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.3} + 0.2 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.2}+ 0.1 \cdot {\rm lg}\hspace{0.1cm}\frac{1}{0.1} \right ] = 1.845\,{\rm bit} \hspace{0.05cm}.\end{align*}$$
Oft ist der Umweg über den Zehnerlogarithmus lg $x = {\rm log}_{10} \ x$ sinnvoll, da meist der Logarithmus dualis $ {\rm log}_2 \ x$ (wird im Folgenden manchmal auch als $ {\rm ld} \ x$ bezeichnet) auf Taschenrechnern nicht zu finden ist.
Bestehen zwischen den einzelnen Symbolwahrscheinlichkeiten Symmetrien wie im Beispiel
- $$p_{\rm A} = p_{\rm D} = p \hspace{0.05cm},\hspace{0.2cm}p_{\rm B} = p_{\rm C} = 0.5-p \hspace{0.05cm},\hspace{0.3cm}{\rm mit} \hspace{0.15cm}0 \le p \le 0.5 \hspace{0.05cm},$$
so kann zur Entropieberechnung auf die binäre Entropiefunktion zurückgegriffen werden:
- $$H_{\rm quat} = 2 \cdot p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm}} + 2 \cdot (0.5-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{0.5-p} = 1 + H_{\rm bin}(2p) \hspace{0.05cm}.$$
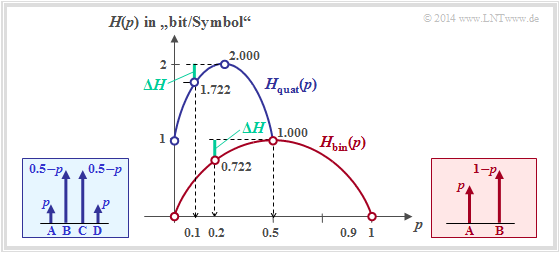
Die Grafik zeigt den Entropieverlauf der Quaternärquelle (blau) im Vergleich zur Binärquelle (rot) abhängig von $p$. Für die Quaternärquelle ist allerdings nur der Abszissenbereich $0 ≤ p ≤ 0.5$ zulässig.
Man erkennt aus der blauen Kurve für die Quaternärquelle:
- Die maximale Entropie $H_\text{max} = 2 \; \rm bit$ ergibt sich für $p = 0.25$ ⇒ $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm A} = 0.25$, also wieder für gleichwahrscheinliche Symbole.
- Mit $p = 0$ bzw. $p = 0.5$ entartet die Quaternärquelle zu einer Binärquelle mit $p_{\rm B} = p_{\rm C} = 0.5$ bzw. $p_{\rm A} = p_{\rm D} = 0.5$. In diesem Fall ergibt sich die Entropie zu $H = 1 \; \rm bit$.
- Die Quelle mit $p_{\rm A} = p_{\rm D} = 0.1$ und $p_{\rm B} = p_{\rm C} = 0.4$ weist folgende Entropie und (relative) Redundanz auf:
- $$\begin{align*}H \hspace{-0.1cm} & = \hspace{-0.1cm} 1 + H_{\rm bin} (2p) =1 + H_{\rm bin} (0.2) = 1.722\,{\rm bit}\hspace{0.05cm},\\ {\rm \Delta }H \hspace{-0.1cm} & = \hspace{-0.1cm} {\rm ld}\hspace{0.1cm} M - H =2\,{\rm bit}- 1.722\,{\rm bit} = 0.278\,{\rm bit}\hspace{0.05cm},\\ r \hspace{-0.1cm} & = \hspace{-0.1cm} {\rm \Delta }H/({\rm ld}\hspace{0.1cm} M) = 0.139\hspace{0.05cm}.\end{align*}$$
Die Redundanz der Quaternärquelle mit $p = 0.1$ ist gleich $ΔH = 0.278 \; \rm bit$ und damit genau so groß wie die Redundanz der Binärquelle mit $p = 0.2$.
Anmerkung: Als Pseudoeinheit ist hier stets „bit” angegeben. Genauer wäre „bit/Symbol”.
Aufgaben zum Kapitel
Aufgabe 1.1Z: Binäre Entropiefunktion
Aufgabe 1.2: Entropie von Ternärquellen
Quellenverzeichnis
- ↑ Shannon, C.E.: A Mathematical Theory of Communication. In: Bell Syst. Techn. J. 27 (1948), S. 379-423 und S. 623-656.