Applets:Physical Signal & Analytic Signal
Inhaltsverzeichnis
Applet Description
This applet shows the relationship between the physical bandpass signal $x(t)$ and the associated analytic signal $x_+(t)$. It is assumed that the bandpass signal $x(t)$ has a frequency-discrete spectrum $X(f)$:
- $$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$
The physical signal $x(t)$ is thus composed of three harmonic oscillations, a constellation that can be found, for example, in the Double-sideband Amplitude Modulation
- of the message signal $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ ⇒ in German: Nachrichtensignal
- with the carrier signal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$ ⇒ in German: Trägersignal.
The nomenclature is also adapted to this case:
- $x_{\rm O}(t)$ denotes the „upper sideband” (in German: Oberes Seitenband) with the amplitude $A_{\rm O}= A_{\rm N}/2$, the frequency $f_{\rm O} = f_{\rm T} + f_{\rm N}$ and the phase $\varphi_{\rm O} = \varphi_{\rm T} + \varphi_{\rm N}$.
- Similarly, for the „lower sideband” (in German: Unteres Seitenband) $x_{\rm U}(t)$ with $f_{\rm U} = f_{\rm T} + f_{\rm N}$, $A_{\rm U}= A_{\rm O}$ and $\varphi_{\rm U} = -\varphi_{\rm O}$.
The associated analytical signal is:
- $$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$
The program displays $x_+(t)$ as the vectorial sum of three rotating pointers (all with positive rotation) as a violet dot (see example graphic for start time $t=0$):
- The (red) pointer of the carrier $x_{\rm T+}(t)$ with length $A_{\rm T}$ and zero phase position $\varphi_{\rm T} = 0$ rotates at constant angular velocity $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}$ (one revolution in time $1/f_{\rm T})$.
- The (blue) pointer of the upper sideband $x_{\rm O+}(t)$ with length $A_{\rm O}$ and zero phase position $\varphi_{\rm O}$ rotates at the angular velocity $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}$, which is slightly faster than $x_{\rm T+}(t)$.
- The (green) pointer of the lower sideband $x_{\rm U+}(t)$ with length $A_{\rm U}$ and zero phase position $\varphi_{\rm U}$ rotates at the angular velocity $2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}$, which is slightly faster than $x_{\rm T+}(t)$.
The time course of $x_+(t)$ is also referred to below as Pointer Diagram. The relationship between the physical bandpass signal $x(t)$ and the associated analytic signal $x_+(t)$ is:
- $$x(t) = {\rm Re}\big [x_+(t)\big ].$$
Note: The graphic applies to $\varphi_{\rm O} = +30^\circ$. From this follows for the start time $t=0$ the angle with respect to the coordinate system: $\phi_{\rm O}=-\varphi_{\rm O}=-30^\circ$. Similarly, from the null phantom $\varphi_{\rm U}=-30^\circ$ of the lower sideband follows for the phase angle to be considered in the complex plane: $\phi_{\rm U}=+30^\circ$.
Theoretical Background
Description of bandpass signals
We consider bandpass signals $x(t)$ with the property that their spectra $X(f)$ are not in the range around the frequency $f=0$, but by a carrier frequency $f_{\rm T}$. In most cases it can also be assumed that the bandwidth is $B \ll f_{\rm T}$.
The figure shows such a bandpass spectrum $X(f)$. Assuming that the associated $x(t)$ is a physical signal and thus real, the spectral function $X(f)$ has a symmetry with respect to the frequency $f = 0$ ⇒ $x(t)$ is an even function ⇒ $x(-t)=x(t)$, so $X(f)$ is real and even.
Beside the physical signal $x(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X(f)$ we use for the description of Bandpass signals alike:
- the analytic signal $x_+(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_+(f)$, see next page,
- the equivalent low-pass –signal (in German: äquivalentes TiefPass–Signal) $x_{\rm TP}(t)\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ X_{\rm TP}(f)$,
see Applet Physical signal and equivalent low pass –signal.
Analytical signal – Frequency domain
The analytic signal $x_+(t)$ belonging to the physical signal $x(t)$ is the time function whose spectrum fulfills the following property:
- $$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot X(f) \; \hspace{0.2cm}\rm for\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm for\hspace{0.2cm} {\it f} < 0.} }\right.$$
The signum function is for positive values of $f$ equal to $+1$ and for negative $f$ values equal to $-1$.
- The (double-sided) limit returns $\sign(0)=0$.
- The index „+” should make it clear that $X_+(f)$ only has shares at positive frequencies.
From the graph you can see the calculation rule for $X_+(f)$: The actual band pass spectrum $X(f)$ becomes
- Doubled at the positive frequencies, and
- set to zero at the negative frequencies.
Due to the asymmetry of $X_+(f)$ with respect to the frequency $f=0$, it can already be said that the time function $x_+(t)$ except for a trivial special case $x_+(t)=0 \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_+(f)=0$ is always complex.
Analytical signal – Time domain
At this point it is necessary to briefly discuss another spectral transformation.
$\text{Definition:}$ For the Hilbert transformed $ {\rm H}\left\{x(t)\right\}$ of a time function $x(t)$ we have::
- $$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau} }\hspace{0.15cm} {\rm d}\tau.$$
This particular integral is not solvable in a simple, conventional way, but must be evaluated using the Cauchy principal value theorem.
Accordingly, in the frequency domain:
- $$Y(f) = {\rm -j \cdot sign}(f) \cdot X(f) \hspace{0.05cm} .$$
The above result can be summarized with this definition as follows:
- The analytic signal $x_+(t)$ is obtained from the physical bandpass signal $x(t)$ by adding an imaginary part to $x(t)$ according to the Hilbert transform:
- $$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$
- $\text{H}\{x(t)\}$ disappears only for the case $x(t) = \rm const.$. For all other signal forms, the analytic signal $x_+(t)$ is complex.
- From the analytic signal $x_+(t)$, the physical bandpass signal can be easily determined by the following operation:
- $$x(t) = {\rm Re}\big[x_+(t)\big] .$$
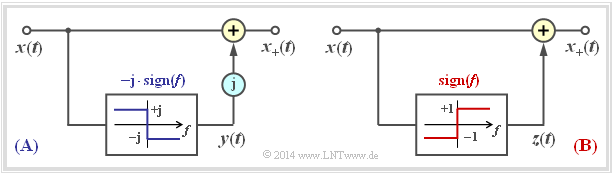
$\text{Example 1:}$ The principle of the Hilbert transformation should be further clarified by the following graphic:
- After the left representation $\rm(A)$ one gets from the physical signal $x(t)$ to the analytic signal $x_+(t)$, by adding an imaginary part ${\rm j} \cdot y(t)$.
- Here $y(t) = {\rm H}\left\{x(t)\right\}$ is a real time function that can be indicated in the spectral domain by multiplying the spectrum $X(f)$ with ${\rm - j} \cdot \sign(f)$.
The right representation $\rm(B)$ is equivalent to $\rm(A)$. Now $x_+(t) = x(t) + z(t)$ stand with the purely imaginary function $z(t)$. A comparison of the two pictures shows that in fact $z(t) = {\rm j} \cdot y(t)$.
Representation of the harmonic oscillation as an analytical signal
The spectral function $X(f)$ of a harmonic oscillation $x(t) = A\cdot\text{cos}(2\pi f_{\rm T}\cdot t - \varphi)$ is known to consist of two dirac functions in the frequencies
- $+f_{\rm T}$ with the complex weight $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$,
- $-f_{\rm T}$ with the complex weight $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$.
Thus, the spectrum of the analytic signal (that is, without the Dirac function at the frequency $f =-f_{\rm T}$, but doubling at $f =+f_{\rm T}$):
- $$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm T}) .$$
The associated time function is obtained by applying the Displacement law:
- $$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$
This equation describes a pointer rotating at constant angular velocity $\omega_{\rm T} = 2\pi f_{\rm T}$.
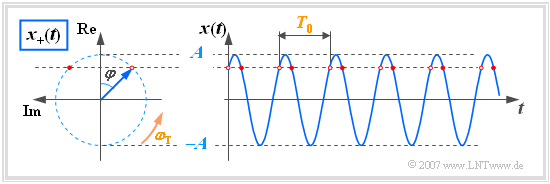
$\text{Example 2:}$ Here the coordinate system is rotated by $90^\circ$ (real part up, imaginary part to the left) contrary to the usual representation.
Based on this graphic, the following statements are possible:
- At the start time $t = 0$, the pointer of length $A$ (signal amplitude) lies with the angle $-\varphi$ in the complex plane. In the example shown, $\varphi=45^\circ$.
- For times $t>0$, the constant angular velocity vector $\omega_{\rm T}$ rotates in a mathematically positive direction, that is, counterclockwise.
- The tip of the pointer is thus always on a circle with radius $A$ and needs exactly the time $T_0$, i.e. the period of the harmonic oscillation $x(t)$ for one revolution.
- The projection of the analytic signal $x_+(t)$ on the real axis, marked by red dots, gives the instantaneous values of $x(t)$.
Analytical signal representation of a sum of three harmonic oscillations
In our applet, we always assume a set of three rotating pointers. The physical signal is:
- $$x(t) = x_{\rm U}(t) + x_{\rm T}(t) + x_{\rm O}(t) = A_{\rm U}\cdot \cos\left(2\pi f_{\rm U}\cdot t- \varphi_{\rm U}\right)+A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t- \varphi_{\rm T}\right)+A_{\rm O}\cdot \cos\left(2\pi f_{\rm O}\cdot t- \varphi_{\rm O}\right). $$
- Each of the three harmonic oscillations $x_{\rm T}(t)$, $x_{\rm U}(t)$ and $x_{\rm O}(t)$ is represented by an amplitude $(A)$, a frequency $(f)$ and a phase value $(\varphi)$.
- The indices are based on Double sideband Amplitude Modulation method. „T” stands for „carrier”, „U” for „lower sideband” and „O” for „Upper Sideband”.
- Similarly, $f_{\rm U} < f_{\rm T}$ and $f_{\rm O} > f_{\rm T}$. There are no restrictions for the amplitudes and phases.
The associated analytical signal is:
- $$x_+(t) = x_{\rm U+}(t) + x_{\rm T+}(t) + x_{\rm O+}(t) = A_{\rm U}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm U}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm U})} \hspace{0.1cm}+ \hspace{0.1cm}A_{\rm T}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm T})} \hspace{0.1cm}+\hspace{0.1cm} A_{\rm O}\cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm O}\hspace{0.05cm}\cdot \hspace{0.05cm}t- \varphi_{\rm O})}. $$
$\text{Example 3:}$ For example the constellation given here results in the double sideband amplitude modulation of the message signal $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t- \varphi_{\rm N}\right)$ with the carrier signal $x_{\rm T}(t) = A_{\rm T}\cdot \cos\left(2\pi f_{\rm T}\cdot t - \varphi_{\rm T}\right)$. This is discussed more frequently in the Exercises.
There are some limitations to the program parameters in this approach:
- For the frequencies always apply $f_{\rm O} = f_{\rm T} + f_{\rm N}$ und $f_{\rm U} = f_{\rm T} - f_{\rm N}$.
- Without distortions the amplitude of the sidebands are $A_{\rm O}= A_{\rm U}= A_{\rm N}/2$.
- The respective phase relationships can be seen in the following graphic.
Exercises
- First select the task number.
- A task description is displayed.
- Parameter values are adjusted.
- Solution after pressing „Hide solition”.
The number „0” will reset to the same setting as the program start and will output a text with further explanation of the applet.
In the following, $\rm Green$ denotes the lower sideband ⇒ $\big (A_{\rm U}, f_{\rm U}, \varphi_{\rm U}\big )$,
$\rm Red$ the carrier ⇒ $\big (A_{\rm T}, f_{\rm T}, \varphi_{\rm T}\big )$ and
$\rm Blue$ the upper sideband ⇒ $\big (A_{\rm O}, f_{\rm O}, \varphi_{\rm O}\big )$.
(1) Consider and interpret the analytic signal $x_+(t)$ for $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1.5\ \text{V}, \ f_{\rm T} = 50 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$. In addition, $A_{\rm U} = A_{\rm O} = 0$.
- Which Signal values $x_+(t)$ result for $t = 0$, $t = 5 \ \rm µ s$ and $t = 20 \ \rm µ s$? How lange are the corresponding signal values of $x(t)$?
- For a cosine signal $x_+(t= 0) = A_{\rm T} = 1.5\ \text{V}$. Then $x_+(t)$ rotates in a mathematically positive direction (one revolution per period $T_0 = 1/f_{\rm T}$):
- $x_+(t= 20 \ {\rm µ s}) = x_+(t= 0) = 1.5\ \text{V}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}x(t= 20 \ {\rm µ s}) = 1.5\ \text{V,}\hspace{0.5cm} x_+(t= 5 \ {\rm µ s}) = {\rm j} \cdot 1.5\ \text{V}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}x(t= 5 \ {\rm µ s}) = {\rm Re}[x_+(t= 5 \ {\rm µ s})] = 0$.
(2) How do the ratios change for $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1.0\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 90^\circ$?
- The signal $x(t)$ is now a sine signal with a smaller amplitude. The analytic signal now starts because of $\varphi_{\rm T} = 90^\circ$ ⇒ $\phi_{\rm T} = -90^\circ$ bei $x_+(t= 0) = -{\rm j} \cdot A_{\rm T}$. After that, $x_+(t)$ rotates again in a mathematically positive direction, but twice as fast because of $T_0 = 10 \ \rm µ s$ as in $\rm (1)$.
(3) Now applies $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = 0^\circ$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.4\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 0^\circ$.
- Consider and interpret the physical signal $x(t)$ the analytic signal $x_+(t)$.
- The Signal $x(t)$ results in the double sideband–Amplitude modulation (ZSB–AM) of the message signals $A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$ with $A_{\rm N} = 0.8\ \text{V}$, $f_{\rm N} = 20\ \text{kHz}$. The carrier $x_{\rm T}(t)$ with $f_{\rm T} = 100\ \text{kHz}$ is also cosinusoidal. The degree of modulation is $m = A_{\rm N}/A_{\rm T} = 0.8$ and the period $T_{\rm 0} = 50\ \text{µs}$.
- In the phasor diagram, the (red) carrier rotates faster than the (green) lower sideband and slower than the (blue) upper sideband. The analytic signal $x_+(t)$ results as the geometric sum of the three rotating hands. It seems that the blue pointer is leading the wearer and the green pointer is following the wearer.
(4) The settings of task (3)continue to apply. Which signal values are obtained at $t=0$, $t=2.5 \ \rm µ s$, $t= 5 \ \rm µ s$ and $t=10 \ \rm µ s$?
- At time $t=0$, all the pointers are in the direction of the real axis, so that $x(t=0) = {\rm Re}\big [x+(t= 0)\big] = A_{\rm U} + A_{\rm T} + A_{\rm O} = 1.8\ \text{V}$.
- Until the time $t=2.5 \ \rm µ s$, the red carrier has rotated by $90^\circ$, the blue pointer by $108^\circ$ and the green by $72^\circ$. We have $x(t=2.5 \ \rm µ s) = {\rm Re}\big [x_+(t= 2.5 \ \rm µ s)\big] = 0$, because now the pointer group points in the direction of the imaginary axis. The other sought signal values are $x(t=5 \ \rm µ s) = {\rm Re}\big [x_+(t= 5 \ \rm µ s)\big] = -1.647\ \text{V}$ and $x(t=10 \ \rm µ s) = {\rm Re}\big [x_+(t= 10 \ \rm µ s)\big] = 1.247\ \text{V}$.
- For $x_+(t)$ a spiral shape results, alternating with a smaller radius and then with a larger radius.
(5) How should the phase parameters $\varphi_{\rm T}$, $\varphi_{\rm U}$ and $\varphi_{\rm O}$ be set if both the carrier $x_{\rm T}(t)$ and the message signal $x_{\rm N}(t)$ are sinusoidal?
- The parameter selection $\varphi_{\rm T} = \varphi_{\rm U} = \varphi_{\rm O}=90^\circ$ describes the signals $x_{\rm T}(t) = A_{\rm T}\cdot \sin\left(2\pi f_{\rm T}\cdot t\right)$ and $x_{\rm N}(t) = A_{\rm N}\cdot \cos\left(2\pi f_{\rm N}\cdot t\right)$. If, in addition, the message $x_{\rm N}(t)$ is sinusoidal, then $\varphi_{\rm O}=\varphi_{\rm T} - 90^\circ = 0$ and $\varphi_{\rm U}=\varphi_{\rm T} + 90^\circ = 180^\circ$ must be set.
(6) The settings of task (3) apply except $A_{\rm T} = 0.6\ \text{V}$. Which modulation method is described here?
- What are the consequences of this? What changes with $A_{\rm T} = 0$?
- It is a ZSB–AM with carrier with the modulation degree $m=0.8/0.6 = 1.333$. For $m > 1$, however, synchronous demodulation is required. envelope detection no longer works.
- With $A_{\rm T} = 0$ ⇒ $m \to \infty$ results in a ZSB–AM without carrier. Also for this you absolutely need the synchronous demodulation.
(7) Now applies $\text{Red:} \hspace{0.15cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.15cm} A_{\rm U} = 0$, $\text{Blue:} \hspace{0.15cm} A_{\rm O} = 0.8\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = 90^\circ$.
- Which constellation is described here? What changes with $A_{\rm U} = 0.8\ \text{V}$ und $A_{\rm O} = 0$?
- In both cases, it is a Single sideband (ESB–AM) with the modulation degree $\mu = 0.8$ (in ESB we denote the degree of modulation with $\mu$ instead $m$). he carrier signal is cosinusoidal and the message signal is sinusoidal.
- $A_{\rm O} = 0.8\ \text{V}$, $A_{\rm U} = 0$ is an OSB modulation. The green pointer is missing and the blue pointer rotates faster compared to the red carrier.
- $A_{\rm U} = 0.8\ \text{V}$, $A_{\rm O} = 0$ is a USB modulation. The blue pointer is missing and the green pointer rotates slower compared to the red carrier.
(8) Now applies $\text{Red:} \hspace{0.05cm} A_{\rm T} = 1\ \text{V}, \ f_{\rm T} = 100 \ \text{kHz}, \ \varphi_{\rm T} = 0^\circ$, $\text{Green:} \hspace{0.05cm} A_{\rm U} = 0.4\ \text{V}, \ f_{\rm U} = 80 \ \text{kHz}, \ \varphi_{\rm U} = -90^\circ$, $\text{Blue:} \hspace{0.05cm} A_{\rm O} = 0.2\ \text{V}, \ f_{\rm O} = 120 \ \text{kHz}, \ \varphi_{\rm O} = +90^\circ$.
- Which constellation could be described here? Which figure is given for the equivalent lowpass–signal $x_{\rm TP}(t)$? ⇒ „locus”?
- It could be a ZSB–AM of a sinusoidal signal with cosinusoidal carrier and modulation degree $m=0.8$, in which the upper sideband is attenuated by a factor of 2. The equivalent lowpass–signal $x_{\rm TP}(t)$ has an elliptical course in the complex plane.
Applet Manual
(A) Parametereingabe für das Eingangssignal $x(t)$ per Slider: Amplituden, Frequenzen, Phasenwerte
(B) Vorauswahl für die Kanalparameter: per Slider, Tiefpass oder Hochpass
(C) Eingabe der Kanalparameter per Slider: Dämpfungsfaktoren und Phasenlaufzeiten
(D) Eingabe der Kanalparameter für Hoch– und Tiefpass: Ordnung $n$, Grenzfrequenz $f_0$
(E) Eingabe der Matching–Parameter $k_{\rm M}$ und $\varphi_{\rm M}$
(F) Auswahl der darzustellenden Signale: $x(t)$, $y(t)$, $z(t)$, $\varepsilon(t)$, $\varepsilon^2(t)$
(G) Graphische Darstellung der Signale
(H) Eingabe der Zeit $t_*$ für die Numerikausgabe
( I ) Numerikausgabe der Signalwerte $x(t_*)$, $y(t_*)$, $z(t_*)$ und $\varepsilon(t_*)$
(J) Numerikausgabe des Hauptergebnisses $P_\varepsilon$
(K) Abspeichern und Zurückholen von Parametersätzen
(L) Bereich für die Versuchsdurchführung: Aufgabenauswahl, Aufgabenstellung und Musterlösung
(M) Variationsmöglichkeiten für die grafische Darstellung
$\hspace{1.5cm}$Zoom–Funktionen „$+$” (Vergrößern), „$-$” (Verkleinern) und $\rm o$ (Zurücksetzen)
$\hspace{1.5cm}$Verschieben mit „$\leftarrow$” (Ausschnitt nach links, Ordinate nach rechts), „$\uparrow$” „$\downarrow$” und „$\rightarrow$”
$\hspace{1.5cm}$Andere Möglichkeiten:
$\hspace{1.5cm}$Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
$\hspace{1.5cm}$Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
About the Authors
This interactive calculation was designed and realized at the Lehrstuhl für Nachrichtentechnik of the Technischen Universität München .
- The original version was created in 2005 by Ji Li as part of her Diploma thesis using „FlashMX–Actionscript” (Supervisor: Günter Söder).
- In 2018 this Applet was redesigned and updated to „HTML5” by Xiaohan Liu as part of her Bachelor's thesis (Supervisor: Tasnád Kernetzky).