Aufgabe 1.3: Fiktive Uni Irgendwo
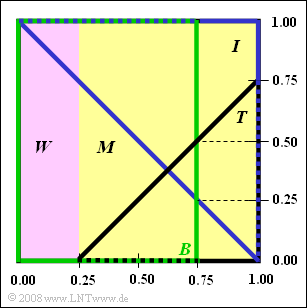
Aus nebenstehender Grafik können Sie einige Informationen über die FUI (Fiktive Universität Irgendwo) ablesen. Das gesamte Quadrat steht für die Grundmenge $G$ der 960 Studierenden. Von diesen sind
- 25% weiblich (Menge $W$, violettes Rechteck),
- 75% männlich (Menge $M$, gelbes Rechteck).
An der Universität gibt es die Fakultäten für
- Theologie (Menge $T$, schwarzes Dreieck),
- Informationstechnik (Menge $I$, blaues Dreieck),
- Betriebswirtschaft (Menge $B$, grünes Viereck).
Jeder Studierende muss mindestens einer dieser Fakultäten zugeordnet sein, kann jedoch auch gleichzeitig zwei oder drei Fakultäten angehören.
Die Flächen in der obigen Darstellung sind maßstäblich, so dass Sie anhand der angegebenen Zahlenwerte und einfachen geometrischen Überlegungen die (prozentualen) Belegungszahlen leicht angeben können.
Hinweise:
- Die Aufgabe gehört zum Kapitel Mengentheoretische Grundlagen.
- Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das Lernvideo Mengentheoretische Begriffe und Gesetzmäßigkeiten.
Fragebogen
Musterlösung
(1) Aus einfachen geometrischen Überlegungen kommt man zu den Ergebnissen:
- $${\rm Pr}(B) = 3/4 \cdot 1 = 3/4\hspace{0.3cm}(\text{absolut:}\ 720),$$
- $${\rm Pr}(I) = {1}/{2}\cdot 1\cdot 1 = 1/2\hspace{0.3cm}(\text{absolut:} \ 480),$$
- $${\rm Pr}(T) = {1}/{2} \cdot {3}/{4} \cdot {3}/{4} = {9}/{32} \hspace{0.3cm}(\text{absolut:}\ 270)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}N_{\rm T} \;\underline{= 270}.$$
(2) Richtig sind die Lösungsvorschläge 2, 3, 5 und 6 ⇒ die Lösungsvorschläge 1, 4, 7 sind demzufolgefalsch:
- Es gibt auch IT-Studentinnen, wenn auch nur sehr wenige.
- Die Vereinigungsmenge von $B$, $I$ und $T$ ergibt zwar die Grundmenge, aber kein vollständiges System, da nicht alle Kombinationen von $B$, $I$ und $T$ zueinander disjunkt sind.
- Aus dem gleichen Grund ergibt auch die Schnittmenge von $B$, $I$ und $T$ nicht die leere Menge.
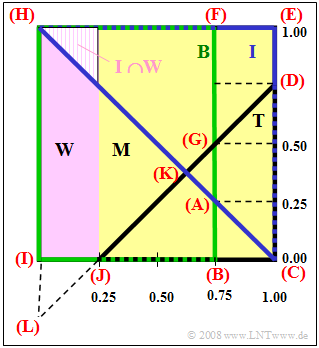
(3) Eine IT-Studentin ist mengentheoretisch die Schnittmenge aus $I$ und $W$ (rechts dargestellt als schraffierte Fläche):
$$\text{Pr[IT-Studentin] = Pr}(I \cap W) = {1}/{2}\cdot {1}/{4} \cdot {1}/{4} = {1}/{32} \underline { \thickapprox 3.13 \%}.$$
In Worten: Unter den 960 Studierenden gibt es 30 IT–Studentinnen.
(4) Die Wahrscheinlichkeit ist als Summe dreier Einzelwahrscheinlichkeiten berechenbar:
$$ \text{Pr[ein Studienfach] = Pr}( \overline{B} \cap \overline{I} \cap T) + {\rm Pr}( \overline{B} \cap I \cap \overline{T}) + {\rm Pr}( \it B \cap \overline{I} \cap \overline{T}).$$
Jede einzelne Wahrscheinlichkeit entspricht einer Fläche im Venndiagramm und kann durch Addition bzw. Subraktion von Dreiecken oder Rechtecken bestimmt werden (siehe Grafik):
- $$p_1 = {\rm Pr}( \overline{B} \cap \overline{I} \cap T) = {\rm Dreieck\ (ABC)}= \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm}\frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm}\frac{1}{4}= \frac{1}{32}\hspace{0.1cm}\underline{\approx 0.0313},$$
- $$p_2 ={\rm Pr}( \overline{B} \cap I \cap \overline{T}) = {\rm Viereck\hspace{0.1cm}(DEFG)}= \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}+ \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4} = \frac{3}{32}\hspace{0.1cm}\underline{\approx 0.0938},$$
- $$p_3 = {\rm Pr}( B \cap \overline{I} \cap \overline{T}) ={\rm Viereck\hspace{0.1cm}(HIJK)}= {\rm Dreieck\hspace{0.1cm}(HLK)}- {\rm Dreieck\hspace{0.1cm}(ILJ)} = \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{4}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{8}\hspace{0.02cm} - \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{1}{4} \cdot \frac{1}{4} = \frac{23}{64}\hspace{0.1cm}\underline{\approx 0.3594}.$$
Oder: $\hspace{0.3cm}p_3 = {\rm Dreieck\hspace{0.1cm}(HIC)}- {\rm Dreieck\hspace{0.1cm}(KJC)} ={1}/{2}\hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} - \hspace{0.1cm}{1}/{2}\hspace{0.05cm} \cdot \hspace{0.1cm} {3}/{4} \cdot {3}/{8} = {23}/{64}.$
Die Summe dieser drei Wahrscheinlichkeiten führt zum Endergebnis $ \text{Pr[ein Studienfach] } = 31/64 \;\underline {\approx 48.43 \%}$.
(5) Diese Wahrscheinlichkeit wird durch das Dreieck (AGK) ausgedrückt. Dieses hat die Fläche $$\rm Pr[drei\hspace{0.1cm}Studienf\ddot{a}cher] = {1}/{2}\cdot {1}/{4}\cdot {1}/{8} = {1}/{64}\hspace{0.15cm}\underline{\approx 1.56 \%}.$$
(6) Die drei Ereignisse „nur ein Studienfach”, „zwei Studienfächer” und
„drei Studienfächer” bilden ein vollständiges System. Damit erhält man mit den Ergebnissen der letzten Teilaufgaben:
- $$\rm Pr[zwei\hspace{0.1cm}Studienf\ddot{a}cher] = 1- \text{Pr[ein Studienfach] } - \rm Pr[drei\hspace{0.1cm}Studienf\ddot{a}cher]= 1- {31}/{64} - {1}/{64} \hspace{0.15cm}\underline{= 50\%}.$$
Zum genau gleichen Ergebnis – aber mit deutlich mehr Aufwand – käme man auf dem direkten Weg entsprechend:
- $$\rm Pr[zwei\hspace{0.1cm}Studienf\ddot{a}cher] = Pr(\it B\cap I \cap\overline{T}) + \rm Pr(\it B\cap\overline{I}\cap{T}) + \rm Pr(\it\overline{B}\cap I \cap T).$$