Eigenschaften von Koaxialkabeln
Inhaltsverzeichnis
Übertragungsmaß von Koaxialkabeln
Koaxialkabel bestehen aus einem Innenleiter und – durch ein Dielektrikum getrennt – einem Außenleiter. Es wurden zwei unterschiedliche Kabeltypen standardisiert, wobei zur Kennzeichnung die Durchmesser von Innen– und Außenleiter genannt werden:
- das Normalkoaxialkabel, dessen Innenleiter einen Durchmesser von $\text{2.6 mm}$ besitzt und dessen Außendurchmesser $\text{9.5 mm}$ beträgt,
- das Kleinkoaxialkabel mit den Abmessungen $\text{1.2 mm}$ und $\text{4.4 mm}$.
Der Kabelfrequenzgang $H_{\rm K}(f)$ ergibt sich aus der Kabellänge $l$ und dem Übertragungsmaß
- $$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot (\beta_1 \cdot f + \beta_2 \cdot \sqrt {f})\hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{-\gamma(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{-\alpha(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l}\hspace{0.05cm}.$$
Die kabelspezifischen Konstanten für das Normalkoaxialkabel $\text{(2.6/9.5 mm)}$ sind:
- $$\begin{align*}\alpha_0 & = 0.00162\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000435\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 21.78\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$
Entsprechend lauten die kilometrischen Dämpfungs– und Phasenkonstanten für das Kleinkoaxialkabel $\text{(1.2/4.4 mm)}$:
- $$\begin{align*}\alpha_0 & = 0.00783\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000443\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.5984\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 22.18\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.5984\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$
Diese Werte können aus den geometrischen Abmessungen der Kabel berechnet werden und wurden durch Messungen am Fernmeldetechnischen Zentralamt in Darmstadt bestätigt – siehe [Wel77][1]. Sie gelten für eine Temperatur von $20^\circ\text{C (293 K)}$ und Frequenzen größer als $\text{200 kHz}$. Es besteht folgender Zusammenhang zu den Leitungsbelägen:
- Die vom frequenzunabhängigem Anteil $R\hspace{0.05cm}’$ herrührenden Ohmschen Verluste werden durch den Parameter $α_0$ modelliert und verursachen eine (bei Koaxialkabeln geringe) frequenzunabhängige Dämpfung.
- Der Anteil $α_1 · f$ des Dämpfungsmaßes ist auf die Ableitungsverluste $(G\hspace{0.05cm}’)$ zurückzuführen und der frequenzproportionale Term $β_1 · f$ bewirkt nur eine Phasenlaufzeit, aber keine Verzerrungen.
- Die Anteile $α_2$ und $β_2$ gehen auf den Skineffekt zurück, der bewirkt, dass bei höherfrequentem Wechselstrom die Stromdichte im Leiterinneren niedriger ist als an der Oberfläche. Dadurch steigt der Widerstandsbelag $R\hspace{0.05cm}’$ einer elektrischen Leitung mit der Wurzel aus der Frequenz an.
Charakteristische Kabeldämpfung
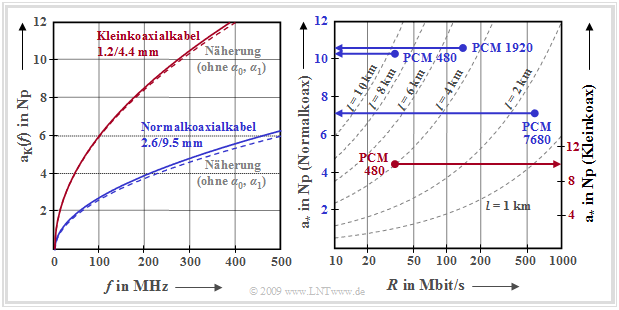
Die Grafik zeigt den frequenzabhängigen Dämpfungsverlauf für das Normalkoaxialkabel und das Kleinkoaxialkabel. Links dargestellt ist die Kabeldämpfung der zwei Koaxialkabeltypen im Frequenzbereich bis $\text{500 MHz}$:
- $${\rm a}_{\rm K}(f) \hspace{-0.05cm} = \hspace{-0.05cm}\big [ \alpha_0 \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_1 \cdot f \hspace{-0.05cm}+ \hspace{-0.05cm} \alpha_2 \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt {f} \hspace{0.01cm} \hspace{0.1cm} \big ] \cdot l \hspace{0.01cm}.$$
Anmerkungen zur grafischen Darstellung:
- Die Ordinatenbeschriftung ist hier in „Np/km” angegeben.
- Oft erfolgt sie auch in „dB/km”, wobei folgende Umrechnung gilt:
- $$1 \ \rm dB = 0.11513\text{...} \ Np,\\ \text{da }\ln(10)/20 = 0.11513\text{...}$$
- Der Dämpfungsverlauf ist hier mit ${\rm a}_{\rm K}(f)$ bezeichnet und nicht mit ${a}_{\rm K}(f)$ ⇒ kursiv, um den Unterschied zwischen dem Dämpfungsmaß „alpha” und der Dämpfungsfunktion „a” (nach Multiplikation mit der Länge) besser erkennbar zu machen.
Man erkennt aus der linken Darstellung, dass der Fehler bei Vernachlässigung des frequenzunabhängigen Anteils $α_0$ und des frequenzproportionalen Terms $(α_1\cdot f)$ noch tolerabel ist. Im Folgenden gehen wir deshalb von der folgenden vereinfachten Dämpfungsfunktion aus:
- $${\rm a}_{\rm K}(f) = \alpha_2 \cdot \sqrt {f} \cdot l = {\rm a}_{\rm \star}\cdot \sqrt { {2f}/{R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{- {\rm a}_{\rm K}(f)}\hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm K}(f)\hspace{0.15cm}{\rm in }\hspace{0.15cm}{\rm Np}\hspace{0.05cm}.$$
$\text{Definition:}$ Als charakteristische Kabeldämpfung $\rm a_∗$ bezeichnen wir die Dämpfung eines Koaxialkabels bei der halben Bitrate unter Vernachlässigung des $α_0$– und des $α_1$–Terms:
- $${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R}/{2}) = \alpha_2 \cdot \sqrt {{R}/{2}} \cdot l\hspace{0.05cm}.$$
Diese Größe eignet sich insbesondere für den Vergleich verschiedener leitungsgebundener Übertragungssysteme mit unterschiedlichen
- Koaxialkabelkabeltypen (zum Beispiel Normal– oder Kleinkoaxialkabel), gekennzeichnet durch den Parameter $\alpha_2$,
- Bitraten $(R)$ und
- Kabellängen $(l)$.
Das rechte Diagramm zeigt die charakteristische Kabeldämpfung $\rm a_∗$ in „Neper” (Np) in Abhängigkeit der Bitrate $R$ und der Kabellänge $l$
- beim Normalkoaxialkabel (linke Ordinatenbeschriftung) und
- beim Kleinkoaxialkabel (rechte Ordinatenbeschriftung).
In dieser Grafik eingezeichnet sind die vom CCITT (Comité Consultatif International Téléphonique et Télégraphique) in den 1970–Jahren vorgeschlagenen PCM–Systeme der Hierarchiestufen $3$ bis $5$. Man erkennt:
- Bei all diesen Systemen zur PCM–Sprachübertragung nimmt die charakteristische Kabeldämpfung Werte zwischen $7 \ \rm Np \ (≈ 61 \ dB)$ und $10.6 \ \rm Np \ (≈ 92 \ dB)$ an.
- Das System $\text{PCM 480}$ – ausgelegt für 480 gleichzeitige Telefonate – mit der Bitrate $R ≈ 35 \ \rm Mbit/s$ wurde sowohl für das Normalkoaxialkabel $($mit der Leitungslänge $l = 9.3 \ \rm km)$ als auch für das Kleinkoaxialkabel $($mit $l = 4 \ \rm km)$ spezifiziert. Die $\rm a_∗$–Werte $10.4\ \rm Np$ bzw. $9.9\ \rm Np$ liegen in der gleichen Größenordnung.
- Das Übertragungssystem $\text{PCM 1920}$ der vierten Hierarchiestufe (spezifiziert für das Normalkoaxialkabel) mit $R ≈ 140 \ \rm Mbit/s$ und $l = 4.65 \ \rm km$ wird durch $\rm a_∗ = 10.6 \ \rm Np$ bzw. $10.6 · 8.688 \ \rm dB/Np ≈ 92\ \rm dB$ parametrisiert.
- Obwohl das System $\text{PCM 7680}$ demgegenüber zwar die vierfache Kapazität $R ≈ 560 \ \rm Mbit/s$ aufweist, ist die charakteristische Kabeldämpfung mit $\rm a_∗ ≈ 61 \ dB$ aufgrund des besseren Mediums „Normalkoaxialkabel” und der um den Faktor $3$ kürzeren Kabelabschnitte $(l = 1.55 \ \rm km)$ deutlich geringer.
- Aus diesen Zahlenwerten geht auch hervor, dass bei Koaxialkabelsystemen die Kabellänge $l$ kritischer ist als die Bitrate $R$. Will man die Kabellänge verdoppeln, muss man die Bitrate um den Faktor $4$ herabsetzen.
Die hier beschriebene Thematik können Sie sich mit dem interaktiven Applet Dämpfung von Kupferkabeln verdeutlichen.
Impulsantwort eines Koaxialkabels
Zur Berechnung der Impulsantwort können von den fünf Anteilen des Übertragungsmaßes die beiden ersten Dämpfungsanteile vernachlässigt werden (die Begründung finden Sie im vorherigen Abschnitt):
- $$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \approx {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \hspace{0.05cm}.$$
Unter Berücksichtigung
- der Kabellänge $l$,
- der charakteristischen Kabeldämpfung $\rm a_∗$ und
- der Tatsache, dass $α_2$ (in Np) und $β_2$ (in rad) zahlenmäßig gleich sind,
gilt somit für den Frequenzgang des Koaxialkabels:
- $$H_{\rm K}(f) = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{2f/R} }\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.02cm} \sqrt{2f/R}}= {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R}} \hspace{0.05cm}.$$
Hierbei sind folgende Abkürzungen verwendet:
- $$b_1\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm rad)}= \beta_1 \cdot l \hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm \star}\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm Np)}= \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$$
Zur Zeitbereichsdarstellung kommt man durch Anwendung der Fourierrücktransformation und des Faltungssatzes:
- $$h_{\rm K}(t) = \mathcal{F}^{-1} \left \{ {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f}\right \} \star\mathcal{F}^{-1} \left \{ {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R} }\right \} \hspace{0.05cm}.$$
Zu berücksichtigen ist hierbei:
- Der erste Term liefert die um die Phasenlaufzeit $τ_{\rm P} = b_1/2π$ verschobene Diracfunktion $δ(t – τ_{\rm P})$.
- Der zweite Term lässt sich analytisch geschlossen angeben. Wir schreiben hierfür $h_{\rm K}(t + τ_P)$. Im Gegensatz zu $h_{\rm K}(t)$ ist hier die Phasenlaufzeit $τ_{\rm P}$ nicht berücksichtigt.
- $$h_{\rm K}(t + \tau_{\rm P}) = \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \hspace{0.05cm}R \hspace{0.05cm}t^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \hspace{0.05cm}R\hspace{0.05cm} t}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$
- Da die Bitrate $R$ bereits bei der Definition der charakteristischen Kabeldämpfung $a_∗$ berücksichtigt wurde, lässt sich diese Gleichung mit der normierten Zeit $t\hspace{0.05cm}' = t/T$ einfach darstellen, wobei $T = 1/R$ die Symboldauer eines Binärsystems angibt. Desweiteren gilt $τ_{\rm P} \hspace{0.05cm}' = τ_{\rm P}/T:$
- $$h_{\rm K}(t\hspace{0.05cm}' + \tau_{\rm P}\hspace{0.05cm} ') = \frac {1}{T} \cdot \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \hspace{0.05cm}t\hspace{0.05cm}'\hspace{0.05cm}^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \hspace{0.05cm}t\hspace{0.05cm}'}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$
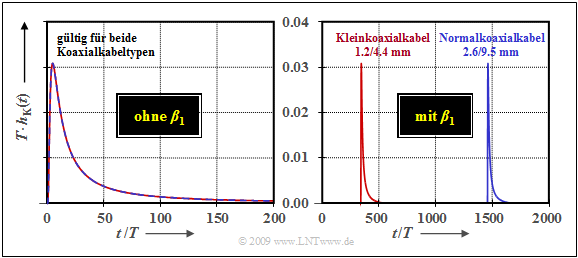
$\text{Beispiel 1:}$ Die Ergebnisse dieser Seite werden durch die folgende Grafik beispielhaft verdeutlicht.
- Dargestellt ist die normierte Impulsantwort $T · h_{\rm K}(t)$ eines Koaxialkabels mit $\rm a_∗ = 60 \ dB \ (6.9\ Np)$.
- Die Dämpfungsmaßparameter $α_0$ und $α_1$ sind somit vernachlässigt.
- Für die linke Grafik wurde zudem der Parameter $β_1 = 0$ gesetzt.
Wegen der Parametrisierung mittels der charakteristischen Kabeldämpfung $a_∗$ und der Normierung der Zeit auf die Symboldauer $T$ gilt die linke Kurve für Systeme mit Klein– bzw. Normalkoaxialkabel, unterschiedliche Längen und verschiedene Bitraten gleichermaßen, zum Beispiel für ein
- Normalkoaxialkabel 2.6/9.5 mm, Bitrate $R = 140 \ \rm Mbit/s$, Kabellänge $l = 3 \ \rm km$ ⇒ System $\rm A$,
- Kleinkoaxialkabel 1.2/4.4 mm, Bitrate $R = 35 \ \rm Mbit/s$, Kabellänge $l = 2.8 \ \rm km$ ⇒ System $\rm B$.
Man erkennt, dass sich selbst bei dieser moderaten Kabeldämpfung $\rm a_∗ = 60 \ \rm dB$ die Impulsantwort aufgrund des Skineffektes $(α_2 = β_2 ≠ 0$) schon über mehr als 200 Symboldauern erstreckt. Da das Integral über $h_{\rm K}(t)$ gleich $H_{\rm K}(f = 0) = 1$ ist, wird der Maximalwert sehr klein:
- $${\rm Max}[h_{\rm K}(t)] \approx 0.03.$$
In der rechten Grafik sind die Auswirkungen des Phasenparameters $β_1$ zu sehen. Beachten Sie bitte die unterschiedlichen Zeitmaßstäbe in der linken und der rechten Darstellung:
- Beim System $\rm A$ $(β_1 = 21.78 \ \rm rad/(km · MHz)$, $T = 7.14\ \rm ns$) führt $β_1$ zu einer Laufzeit von
- $$\tau_{\rm A}= \frac {\beta_1 \cdot l}{2\pi} =\frac {21.78\, { {\rm rad} }/{ {(\rm km \cdot MHz)} }\cdot 3\,{\rm km} }{2\pi} = 10.4\,{\rm \mu s}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\tau_{\rm A}\hspace{0.05cm}'' = {\tau_{\rm A} }/{T} \approx 1457\hspace{0.05cm}.$$
- Dagegen erhält man für das System $\rm B$ $(β_1 = 22.18 \ \rm rad/(km · MHz)$, $T = 30 \ \rm ns$):
- $$\tau_{\rm B}= \frac {\beta_1 \cdot l}{2\pi} =\frac {22.18\, { {\rm rad} }/{ {(\rm km \cdot MHz)} }\cdot 2.8\,{\rm km} }{2\pi} = 9.9\,{\rm µ s}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\tau_{\rm B}\hspace{0.05cm}' ={\tau_{\rm B} }/{T} \approx 330\hspace{0.05cm}.$$
Obwohl bei den getroffenen Annahmen $τ_{\rm A} ≈ τ_{\rm B}$ gilt, ergeben sich wegen der Zeitnormierung auf $T = 1/R$ völlig unterschiedliche Verhältnisse.
$\text{Fazit:}$ Bei der Simulation und Optimierung von Nachrichtensystemen verzichtet man meist auf den Phasenterm mit $b_1 = β_1 · l$, da dieser ausschließlich eine (oft nicht störende) Laufzeit zur Folge hat, aber keine Signalverzerrung.
Empfangsgrundimpuls
Mit dem Sendegrundimpuls $g_s(t)$ und der Impulsantwort $h_{\rm K}(t)$ ergibt sich für den Empfangsgrundimpuls:
- $$g_r(t) = g_s(t) \star h_{\rm K}(t)\hspace{0.05cm}.$$
Verwendet man am Sender einen NRZ–Rechteckimpuls $g_s(t)$ mit der Amplitude $s_0$ und Dauer $Δt_s = T$, so ergibt sich für den Grundimpuls am Ausgang des Koaxialkabels:
- $$g_r(t) = 2 s_0 \cdot \left [ {\rm Q} \left (\frac {{\rm a}_{\rm \star}/\sqrt {\pi}}{ \sqrt{ (t/T - 0.5)}}\right ) - {\rm Q} \left (\frac {{\rm a}_{\rm \star}/\sqrt {\pi}}{ \sqrt{ (t/T + 0.5)}}\right ) \right ]\hspace{0.05cm}.$$
Hierbei bezeichnet $\rm a_∗$ die charakteristische Kabeldämpfung in Neper und ${\rm Q}(x)$ die komplemantäre Gaußsche Fehlerfunktion.
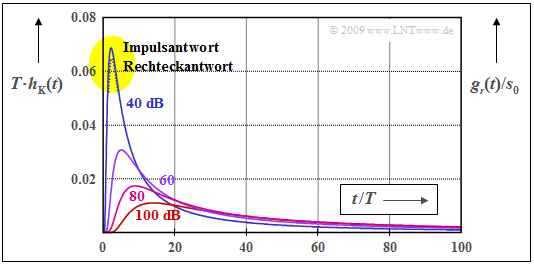
$\text{Beispiel 2:}$ Die Abbildung zeigt für die charakteristischen Kabeldämpfungen $\rm a_∗ = 40 \ \rm dB$, $60 \ \rm dB$, $80 \ \rm dB$ und $100 \ \rm dB$
- die normierte Koaxialkabelimpulsantwort $T · h_{\rm K}(t)$ ⇒ Impulsantwort (durchgezogene Kurven), und
- den auf die Sendeamplitude $s_0$ normierten Empfangsgrundimpuls $g_r(t)$ ⇒ Rechteckantwort (gepunktete Linie).
Kleinere Werte von $\rm a_∗$ sind für die Praxis nicht relevant.
Man erkennt aus dieser Darstellung:
- Mit $\rm a_∗ = 40 \ \rm dB$ ist die normierte Rechteckantwort $g_r(t)/s_0$ an der Spitze geringfügig (etwa um den Faktor 0.95) kleiner als die normierte Impulsantwort $T · h_{\rm K}(t)$. Hier gibt es eine kleine Differenz zwischen Impulsantwort und Rechteckantwort.
- Dagegen sind für den Fall $a_∗ ≥ 60 \ \rm dB$ die Rechteckantwort und die Impulsantwort innerhalb der Zeichengenauigkeit nicht zu unterscheiden.
- Bei einem RZ–Impuls wäre die obige Gleichung für den Empfangsgrundimpuls noch mit dem Tastverhältnis $Δt_s/T$ zu multiplizieren. In diesem Fall ist $g_r(t)/s_0$ mindestens um diesen Faktor kleiner als $T · h_{\rm K}(t)$.
- Die so modifizierte Gleichung stellt auch eine gute Näherung für andere Sendegrundimpulse dar, so lange $\rm a_∗≥ 60 \ \rm dB$ hinreichend groß ist. $Δt_s$ gibt dann die äquivalente Impulsdauer des Sendegrundimpulses an.
Wir weisen Sie an dieser Stelle auf das interaktive Applet Zeitverhalten von Kupferkabeln hin, das die hier behandelte Thematik zum Inhalt hat.
Besonderheiten von Koaxialkabelsystemen
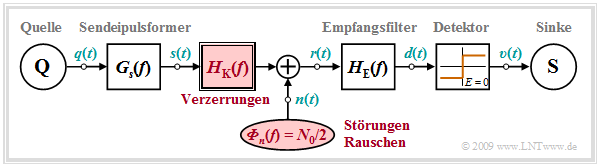
Geht man von binärer Übertragung mit NRZ–Rechteckimpulsen (Symboldauer $T$) und einem koaxialen Übertragungskanal aus, so ergibt sich das folgende Systemmodell:
Insbesondere ist zu beachten:
- Bei einer Simulation lässt man zweckmäßigerweise die Laufzeit des Koaxialkabels außer Betracht. Dann gilt für den Empfangsgrundimpuls $g_r(t)$ mit ${\rm exp} \left [ -A \right ]= {\rm e}^{ -A}$ näherungsweise:
- $$g_r(t) \approx s_0 \cdot T \cdot h_{\rm K}(t) = \frac {s_0 \cdot {\rm a}_{\rm \star}/\pi}{ \sqrt{2 \hspace{0.05cm}(t/T)^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \hspace{0.05cm}t/T}} \right ] \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} {\rm mit}\hspace{0.15cm}{\rm a}_{\rm \star}\hspace{0.15cm} {\rm in}\hspace{0.15cm} {\rm Neper}\hspace{0.05cm}.$$
- Wegen der sehr guten Abschirmung der Koaxialkabel gegenüber anderen Störungen ist hier das thermische Rauschen die dominante Störursache. Das Störsignal $n(t)$ ist in diesem Fall gaußverteilt und weiß und wird durch die (zweiseitige) Rauschleistungsdichte $N_0/2$ beschrieben.
- Der weitaus größte Rauschanteil entsteht in der Eingangsstufe des Empfängers, so dass man $n(t)$ zweckmäßigerweise an der Schnittstelle „Kabel–Empfänger” addiert. Mit den Amplitudenkoeffizienten $a_{\nu}$ gilt dann für das Empfangssignal:
- $$r(t) = \sum_{\nu = - \infty}^{+ \infty}a_{\nu}\cdot g_r(t - \nu \cdot T)+ n(t) \hspace{0.05cm} .$$
- Dieser Störadditionspunkt ist auch deshalb sinnvoll, da alle entlang des Kabels akkumulierten Rauschstörungen durch den Kabelfrequenzgang $H_{\rm K}(f)$ entscheidend gedämpft werden.
Aufgaben zum Kapitel
Aufgabe 4.4: Koaxialkabel – Frequenzgang
Aufgabe 4.5: Koaxialkabel – Impulsantwort
Aufgabe 4.5Z: Nochmals Impulsantwort
Quellenverzeichnis
- ↑ Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.