Aufgabe 1.1: Einfache Filterfunktionen
Man bezeichnet ein Filter mit dem Frequenzgang
- $$H_{\rm TP}(f) = \frac{1}{1+ {\rm j}\cdot f/f_0}$$
als Tiefpass erster Ordnung. Daraus lässt sich ein Hochpass erster Ordnung nach folgender Vorschrift gestalten:
- $$H_{\rm HP}(f) = 1- H_{\rm TP}(f) .$$
In beiden Fällen gibt $f_0$ die so genannte $\text{3 dB}$–Grenzfrequenz an.
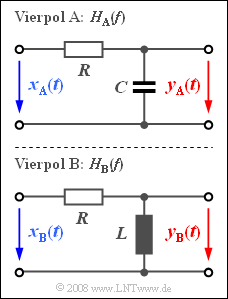
Die Abbildung zeigt zwei Vierpole $\rm A$ und $\rm B$. In der Aufgabe ist zu klären, welcher der beiden Vierpole eine Tiefpass– und welcher eine Hochpasscharakteristik aufweist.
Die Bauelemente von Schaltung $\rm A$ sind wie folgt gegeben:
- $$R = 50 \,\, {\rm \Omega}, \hspace{0.2cm} C = 637 \,\, {\rm nF} .$$
Die Induktivität $L$ von Schaltung $\rm B$ ist in der Teilaufgabe (6) zu berechnen.
Hinweise:
- Die Aufgabe gehört zum Kapitel Systembeschreibung im Frequenzbereich.
- Für die Teilaufgabe (4) werden cosinusförmige Eingangssignale vorausgesetzt. Die Frequenz $f_x$ ist variabel, die Leistung beträgt $P_x = 10\,{\rm mW}.$
Fragebogen
Musterlösung
- Der komplexe Widerstand der Kapazität $C$ ist gleich $1/({\rm j}ωC)$, wobei $ω = 2πf$ die so genannte Kreisfrequenz angibt. Der Frequenzgang lässt sich nach dem Spannungsteilerprinzip berechnen:
- $$H_{\rm A}(f) = \frac{Y_{\rm A}(f)}{X_{\rm A}(f)} = \frac{1/({\rm j}\omega C)}{R+1/({\rm j}\omega C)}=\frac{1}{1+{\rm j \cdot 2\pi}\cdot f \cdot R\cdot C}.$$
- Wegen $H_{\rm A}(f = 0) = 1$ kann dies kein Hochpass sein; vielmehr handelt es sich um einen Tiefpass.
- Bei niedrigen Frequenzen ist der Blindwiderstand der Kapazität sehr groß und es gilt $y_{\rm A}(t) ≈ x_{\rm A}(t)$.
- Dagegen wirkt der Kondensator bei sehr hohen Frequenzen wie ein Kurzschluss und es ist $y_{\rm A}(t) ≈ 0$.
(2) Durch Koeffizientenvergleich zwischen $H_{\rm TP}(f)$ auf der Angabenseite und $H_{\rm A}(f)$ gemäß Teilaufgabe (1) erhält man:
- $$f_0 = \frac{1}{2\pi \cdot R \cdot C} = \frac{1}{2\pi \cdot{\rm 50\hspace{0.05cm} \Omega}\cdot {\rm 637 \cdot 10^{-9}\hspace{0.05cm} s/\Omega}}\hspace{0.15cm}\underline{\approx 5 \, {\rm kHz}}.$$
(3) Der Amplitudengang lautet:
- $$|H_{\rm A}(f)| = \frac{1}{\sqrt{1+ (f/f_0)^2}}.$$
Für $f = f_0$ erhält man den Zahlenwert $1/\sqrt{2}\hspace{0.1cm} \underline{≈ 0.707}$, und für $f = 2f_0$ näherungsweise den Wert $1/\sqrt{5}\hspace{0.1cm} \underline{≈ 0.477}$.
(4) Die Ausgangsleistung kann nach folgender Gleichung berechnet werden:
- $$P_y = P_x \cdot |H_{\rm A}(f = f_x)|^2.$$
Für $f_x = f_0$ ist $P_y = P_x/2 \hspace{0.1cm} \underline{ = 5\hspace{0.1cm} {\rm mW}}$, also ergibt sich am Ausgang nur noch die halbe Leistung.
In logarithmischer Darstellung lautet diese Beziehung:
- $$10 \cdot {\rm lg}\hspace{0.2cm} \frac{P_x(f_0)}{P_y(f_0)} = 3\,{\rm dB}.$$
Deshalb ist für $f_0$ auch die Bezeichnung „3dB–Grenzfrequenz” üblich.
Für $f_x = 2f_0$ erhält man dagegen einen kleineren Wert: $P_y = P_x/5 \hspace{0.1cm}\underline{= 2\hspace{0.1cm} {\rm mW}}$.
(5) Analog zur Teilaufgabe (1) gilt:
- $$H_{\rm B}(f) = \frac{Y_{\rm B}(f)}{X_{\rm B}(f)} = \frac{{\rm j}\omega L}{R+{\rm j}\omega L}=\frac{{\rm j2\pi}\cdot f \cdot L/R}{1+{\rm j2\pi}\cdot f \cdot L/R}.$$
Unter Verwendung der Bezugsfrequenz $f_0 = R/(2πL)$ kann hierfür auch geschrieben werden:
- $$H_{\rm B}(f) = \frac{{\rm j}\cdot f/f_0}{1+{\rm j}\cdot f/f_0}\hspace{0.5cm}\Rightarrow \hspace{0.5cm}|H_{\rm B}(f)| = \frac{|f/f_0|}{\sqrt{1+ (f/f_0)^2}}.$$
Daraus erhält man die Zahlenwerte:
- $$|H_{\rm B}(f = 0)| \hspace{0.15cm}\underline{= 0}, \hspace{0.5cm} |H_{\rm B}( f_0)| \hspace{0.15cm}\underline{=0.707}, \hspace{0.5cm}|H_{\rm B}(2f_0)| \hspace{0.15cm}\underline{= 0.894}, \hspace{0.5cm}|H_{\rm B}(f \rightarrow \infty)|\hspace{0.15cm}\underline{ = 1}.$$
Der Vierpol $\rm B$ ist demzufolge ein Hochpass.
(6) Aus obiger Definition der Bezugsfrequenz folgt:
- $$L = \frac{R}{2\pi \cdot f_0} = \frac{{\rm 50\hspace{0.05cm} \Omega}}{2\pi \cdot{\rm 5000 \hspace{0.05cm} Hz}}= {\rm 1.59 \cdot 10^{-3}\hspace{0.05cm} \Omega s}\hspace{0.15cm}\underline{= {\rm 1.59 \hspace{0.1cm} mH}} .$$