Aufgabe 3.2Z: Zusammenhang zwischen WDF und VTF

• Zurück zum Buch

Verteilungsfunktion  $ F_x(r)$

Gegeben ist die Zufallsgröße  $x$  mit der Verteilungsfunktion

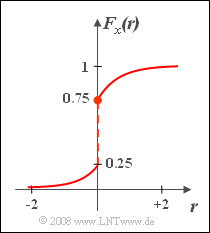
$$ F_x(r)=\left\{\begin{array}{*{4}{c}} 0.25\cdot {\rm e}^{2\it r} &\rm f\ddot{u}r\hspace{0.1cm}\it r<\rm 0, \\ 1-0.25\cdot {\rm e}^{-2\it r} & \rm f\ddot{u}r\hspace{0.1cm}\it r\ge\rm 0. \\\end{array}\right.$$

• Diese Funktion ist rechts dargestellt.
• Es ist zu erkennen, dass an der Sprungstelle  $r = 0$  der rechtsseitige Grenzwert gültig ist.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Verteilungsfunktion.
• Bezug genommen wird auch auf das Kapitel  Wahrscheinlichkeitsdichtefunktion.
• Eine Zusammenfassung der hier behandelten Thematik bietet das Lernvideo  Zusammenhang zwischen WDF und VTF.

Fragebogen

1

Welche Eigenschaften einer Verteilungsfunktion (VTF) gelten allgemein, also nicht nur bei diesem konkreten Beispiel?

	Die VTF steigt von  $0$  auf  $1$  zumindest schwach monoton an.
	Die  $F_x(r)$–Werte  $0$  und  $1$  sind für endliche  $r$–Werte möglich.
	Ein horizontaler Abschnitt weist darauf hin, dass in diesem Bereich die Zufallsgröße keine Anteile besitzt.
	Vertikale Abschnitte sind möglich.

2

Wie groß ist die Wahrscheinlichkeit, dass  $x$  positiv ist?

${\rm Pr}(x > 0) \ = \ $

3

Wie groß ist die Wahrscheinlichkeit, dass  $|\hspace{0.05cm}x\hspace{0.05cm}|$  größer ist als  $0.5$?

${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}| > 0.5) \ = \ $

4

Geben Sie die zugehörige WDF  $f_x(x)$  allgemein an und den Wert für  $x = 1$.

$f_x(x =1)\ = \ $

5

Wie groß ist die Wahrscheinlichkeit, dass  $x$  genau gleich  $1$  ist?

${\rm Pr}(x = 1)\ = \ $

6

Wie groß ist die Wahrscheinlichkeit, dass  $x$  genau gleich  $0$  ist?

${\rm Pr}(x = 0)\ = \ $

Musterlösung

Musterlösung

(1)  Die Aussagen 1, 3 und 4 sind immer richtig:

• Ein horizontaler Abschnitt in der VTF weist darauf hin, dass die Zufallsgröße in diesem Bereich keine Werte besitzt.
• Dagegen weist ein vertikaler Abschnitt in der VTF auf eine Diracfunktion in der WDF (an gleicher Stelle $x_0$) hin.
• Dies bedeutet, dass die Zufallsgröße den Wert $x_0$ sehr häufig annimmt, nämlich mit endlicher Wahrscheinlichkeit.
• Alle anderen Werte treten exakt mit der Wahrscheinlichkeit $0$ auf.
• Ist jedoch $x$ auf den Bereich von $x_{\rm min}$ bis $x_{\rm max}$ begrenzt, so ist $F_x(r) = 0$  für  $r < x_{\rm min}$ und $F_x(r) = 1$  für  $r > x_{\rm max}$.
• In diesem Sonderfall wäre auch die zweite Aussage zutreffend.

(2)  Die gesuchte Wahrscheinlichkeit kann man aus der Differenz der VTF–Werte an den Grenzen berechnen:

$${\rm Pr}( x> 0)= F_x(\infty)- F_x(\rm 0) \hspace{0.15cm}\underline{=\rm 0.25}.$$

WDF der Laplace-Verteilung

(3)  Für die Wahrscheinlichkeit, dass $x$ größer als $0.5$ ist, gilt:

$${\rm Pr}(x> 0.5)=1- F_x(0.5)=\rm 0.25\cdot e^{-1} \hspace{0.15cm}{\approx0.092}. $$

Aus Symmetriegründen ist ${\rm Pr}(x<- 0.5)$ genauso groß. Daraus folgt:

$${\rm Pr}( |\hspace{0.05cm} x\hspace{0.05cm}| >\rm 0.5) \hspace{0.15cm}\underline{= \rm 0.184}.$$

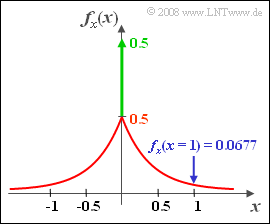
(4)  Die WDF erhält man aus der zugehörigen VTF durch Differenzieren der zwei Bereiche. Es ergibt sich eine zweiseitige Exponentialfunktion sowie eine Diracfunktion bei $x = 0$:

$$f_x(x)=\rm 0.5\cdot \rm e^{-2\cdot |\hspace{0.05cm}\it x\hspace{0.05cm}|} + \rm 0.5\cdot\delta(\it x).$$

Der gesuchte Zahlenwert ist $f_x(x = 1)\hspace{0.15cm}\underline{= \rm 0.0677}$.

Hinweis:   Die zweiseitige Exponentialverteilung nennt man auch „Laplaceverteilung”.

(5)  Im Bereich um $1$ beschreibt $x$ eine kontinuierliche Zufallsgröße. Die Wahrscheinlichkeit, dass $x$ exakt den Wert $1$ aufweist, ist deshalb ${\rm Pr}(x = 1)\hspace{0.15cm}\underline{= \rm 0}.$

(6)  In $50\%$ der Zeit wird $x = 0$ gelten:   ${\rm Pr}(x = 0)\hspace{0.15cm}\underline{= \rm 0.5}.$

Hinweise:

• Die WDF eines Sprachsignals wird häufig durch eine zweiseitige Exponentialfunktion beschrieben.
• Die Diracfunktion bei $x = 0$ berücksichtigt vor allem Sprachpausen – hier in $50\%$ aller Zeiten.