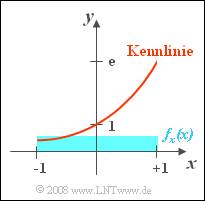
Aufgabe 4.2Z: Korrelation zwischen „x“ und „e hoch x“
Die Zufallsgröße $x$ sei gleichverteilt zwischen $-1$ und $+1$. Damit ist
- der Mittelwert $m_x = 0$, und
- die Varianz $\sigma_x^2 = 1/3$.
Durch die nichtlineare Kennlinie $y = g(x) = {\rm e}^x$ wird die Zufallsgröße $y $ gebildet. Zwischen den beiden Zufallsgrößen $x$ und $y$ besteht also ein fester, deterministischer Zusammenhang und die Zufallsgröße $y$ kann nur Werte zwischen $1/{\rm e}$ und ${\rm e}$ annehmen.
Für die Wahrscheinlichkeitsdichtefunktion erhält man für diesen Bereich nach dem Prinzip „Transformation von Zufallsgrößen”:
- $$f_y(y) = {\rm 1}/({\rm 2\it y}). $$
Hinweise:
- Die Aufgabe gehört zum Kapitel Zweidimensionale Zufallsgrößen.
- Bezug genommen wird auch auf das Kapitel Erwartungswerte und Momente.
- Berücksichtigen Sie, dass im betrachteten Bereich $-1 ≤ x ≤ +1$ die Exponentialfunktion wie folgt angenähert werden kann:
- $$y={\rm e}^{x}\approx 1+ \frac{ x}{1!} + \frac{{ x}^{\rm 2}}{\rm 2!}+ \frac{{x}^{\rm 3}}{\rm 3!}+ \frac{{x}^{\rm 4}}{\rm 4!}.$$
Fragebogen
Musterlösung
- Eine zweite Berechnungsmöglichkeit basiert direkt auf den Rechenregeln für Erwartungswerte:
- $$m_y={\rm E}\big[ y\big] = \int_{-\infty}^{+\infty}g(x) \cdot f_x(x)\,\, {\rm d}x = {1}/{2}\cdot\int_{-1}^{1}{\rm e}^{ x}\,\,{\rm d}x=\rm {1}/{2}\cdot(e-e^{-1}) \hspace{0.15cm}\underline{= 1.175}.$$
(2) Für den quadratischen Mittelwert der Zufallsgröße $y$ gilt:
- $$m_{2 y} = {\rm E}\big[ y^{\rm 2}\big] = {\rm E}[{\rm e}^{ 2 x}]= {1}/{2}\cdot\int_{-1}^{+1}{\rm e}^{2 x} \,\,{\rm d}x = {1}/{4}\cdot({\rm e}^{2}-{\rm e}^{-2}) = 1.813.$$
- Daraus erhält man mit dem Satz von Steiner:
- $$\sigma_y^{\rm 2} = m_{ 2 y}- m_{ y}^2 = {1}/{4}\cdot({\rm e}^{2}-{\rm e}^{-2})-{1}/{4}\cdot( {\rm e}^{2}-2+{\rm e}^{-2})={1}/{2}\cdot(1-{\rm e}^{-2})=0.432 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\sigma_y \hspace{0.15cm}\underline{= 0.658}.$$
(3) Richtig sind die Lösungsvorschläge 1, 3 und 4:
- Außerhalb der Kurve $y = {\rm e}^x$ ist die WDF natürlich Null.
- Da das Volumen unter der 2D-WDF gleich $1$ ist, sind die WDF-Werte für den unendlich schmalen Bereich $y = {\rm e}^x$ unendlich groß.
- Das heißt: Die WDF beschreibt eine gekrümmte Diracwand.
- Aufgrund des Abfalls der WDF $f_y(y)$ mit steigenden $y$ nimmt die Höhe dieser Diracwand von $(-1, 1/{\rm e})$ bis zu $(+1, {\rm e})$ kontinuierlich ab.
(4) Für das gemeinsame Moment gilt:
- $$m_{xy} = {\rm E}\big[ x\cdot y \big] = {\rm E}\big[ x\cdot {\rm e}^{x} \big].$$
- Mit der angegebenen Reihenentwicklung folgt daraus die Näherung:
- $$m_{xy} \approx {\rm E}\big[x\big] + {\rm E}\big[x^{\rm 2}\big] + \frac{1}{2} \cdot {\rm E}\big[ x^{\rm 3}\big] + \frac{1}{6} \cdot {\rm E}\big[ x^{\rm 4}\big]+ \frac{1}{24} \cdot {\rm E}\big[ x^{\rm 5}\big].$$
- Aufgrund der Symmetrie der Zufallsgröße $x$ gilt für alle ungeradzahligen Werte von $k$: $\rm E\big[\it x^{k}\rm \big] =\rm 0.$ Weiterhin gilt:
- $${\rm E}\big[ x^{\rm 2}\big] = \sigma_{x}^{\rm 2}= \frac{1}{3}, \hspace{0.5cm} {\rm E}\big[ x^{\rm 4}\big] = \frac{1}{2}\int_{-1}^{+1} x^{\rm 4} \,\,{\rm d}x = \rm\frac{1}{5}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\it m_{xy}} = \rm\frac{1}{3} + \frac{1}{6}\cdot\frac{1}{5} = \frac{11}{30}\hspace{0.15cm}\underline{\approx 0.367}.$$
(5) Wegen $m_x = 0$ gilt $\mu_{xy} = m_{xy}$. Somit ergibt sich für den Korrelationskoeffizienten:
- $$\it \rho_{xy} = \frac{\mu_{xy}}{\sigma_x \cdot \sigma_y}=\rm\frac{0.367}{0.577 \cdot 0.658}\hspace{0.15cm}\underline{ \approx 0.967}.$$
- Zwischen $x$ und $y$ besteht zwar ein eindeutiger deterministischer Zusammenhang.
- Da aber hierin auch nichtlineare Bindungen enthalten sind, ist der Korrelationskoeffizient $ \rho_{xy} \ne 1$.