Exercise 1.3: Rayleigh Fading

Time evolution of Rayleigh fading

Rayleigh–Fading should be used when

there is no direct connection between transmitter and receiver, and
the signal reaches the receiver through many paths, but their transit times are approximately the same.

An example of such a Rayleigh channel occurs in urban mobile communications when narrow-band signals are used with ranges between $50$ and $100$ meters.

Looking at the radio signals $s(t)$ and $r(t)$ in the equivalent low-pass range $($that is, around the frequency $f = 0)$, the signal transmission is described completely by the equation

$$r(t)= z(t) \cdot s(t)$$

The multiplicative fading coefficient

$$z(t)= x(t) + {\rm j} \cdot y(t)$$

is always complex and has the following characteristics:

The real part $x(t)$ and the imaginary part $y(t)$ are Gaussian mean-free random variables, both with equal variance $\sigma^2$. Within the components $x(t)$ and $y(t)$ there may be statistical dependence, but this is not relevant for the solution of the present task. We assume that $x(t)$ and $y(t)$; are uncorrelated.

The magnitude $a(t) = |z(t)|$ has a Rayleigh PDF, from which the name Rayleigh Fading is derived:

$$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^ { -a^2/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm}.$$

The squared magnitude $p(t) = a(t)^2 = |z(t)|^2$ is exponentially distributed according to the equation

$$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^ { -p/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} \hspace{0.05cm}.$$

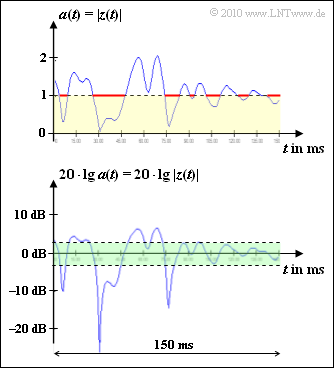
Measurements have shown that the time intervals with $a(t) ≤ 1$ (highlighted in yellow in the graphic) add up to $\text{59 ms}$ (intervals highlighted in red). Being the total measurement time $\text{150 ms}$, the probability that the magnitude of the Rayleigh fading is less than or equal to $1$ is $${\rm Pr}(a(t) \le 1) = \frac{59\,\,{\,{\rm ms}}}{150\,\,{\rm ms}} = 39.4 \% \hspace{0.05cm}.$$

In the lower graph, the value range between $\text{-3 dB}$ and $\text{+3 dB}$ of the logarithmic Rayleigh coefficient $20 \cdot {\rm lg} \ a(t)$ is highlighted in green. The subtask (4) refers to this.

Notes:

This task belongs to chapter Wahrscheinlichkeitsdichte des Rayleigh–Fadings of this book.
A similar topic is treated with a different approach in chapter Weitere Verteilungen of the book „Stochastic Signal Theory”.
To check your results, you can use the interactive applet WDF, VTF and Moments of the book „Stochastic Signal Theory”.

Questionnaire

${\rm Max}\big [20 \cdot {\rm lg} \ {a(t)}\big] \ = \ $

$\ \rm dB$

${\rm Max}\big[p(t)\big] \ = \ $

${\rm Max}\big[10 \cdot {\rm lg} \ p(t)\big] \ = \ $

$ \ \rm dB$

$\sigma \ = \ $

${\rm Pr}(|10 \cdot {\rm lg} \ p(t)| < 3 \ \rm dB) \ = \ $

Sample solution

Musterlösung

(1) From ${\rm Max}[a(t)] = 2$ follows directly:

$${\rm Max} \left [ 20 \cdot {\rm lg}\hspace{0.15cm}a(t) \right ] = 20 \cdot {\rm lg}\hspace{0.15cm}(2) \hspace{0.15cm} \underline{\approx 6\,\,{\rm dB}} \hspace{0.05cm}.$$

(2) The maximum value of the square $p(t) = a(t)^2$ is $${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{=4} \hspace{0.05cm}.$$

The logarithmic representation of the squared magnitude $p(t)$ is identical to the logarithmic representation of the amount $a(t)$. Since $p(t)$ is a power quantity

$${\rm Max} \left [ p(t) \right ] = {\rm Max} \left [ a(t)^2 \right ] \hspace{0.15cm} \underline{= 4} \hspace{0.05cm}.$$

The maximum value is thus also $\underline{\approx 6\,\,{\rm dB}}$.

(3) The condition $a(t) ≤ 1$ is equivalent to the requirement $p(t) = a(t)^2 ≤ 1$.

The absolute square is known to be exponentially distributed, and for $p ≥ 0$ we have

$$f_p(p) = \frac{1}{2\sigma^2} \cdot {\rm exp} [ -\frac{p}{2\sigma^2}] \hspace{0.05cm}.$$

PDF and probability regions

It follows:

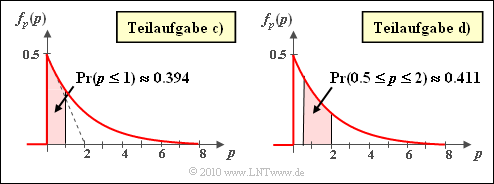
$${\rm Pr}(p(t) \le 1) = \frac{1}{2\sigma^2} \cdot \int_{0}^{1}{\rm exp} [ -\frac{p}{2\sigma^2}] \hspace{0.15cm}{\rm d}p = 1 - {\rm exp} [ -\frac{1}{2\sigma^2}] = 0.394$$ $$\Rightarrow \hspace{0.3cm} {\rm exp} [ -\frac{1}{2\sigma^2}] = 0.606 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \sigma^2 = \frac{1}{2 \cdot {\rm ln}\hspace{0.1cm}(0.606)} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{\sigma = 1} \hspace{0.05cm}.$$

The graph shows

on the left side the probability ${\rm Pr}(p(t) ≤ 1)$,
on the right side the probability ${\rm Pr}(0.5 \le p(t) ≤ 2)$.

'(4) From $10 \cdot {\rm lg} \ p_1 = \ –3 \ \ \rm dB$ follows $p_1 = 0.5$ and the upper limit of the integration range results from the condition $10 \cdot {\rm lg} \ p_2 = +3 \ \ \rm dB$ to $p_2 = 2$.

This gives you, according to the above graphic:

$${\rm Pr}(-3\,\,{\rm dB}\le 10 \cdot {\rm lg}\hspace{0.15cm}p(t) \le +3\,\,{\rm dB}) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{0.5}^{2}f_p(p)\hspace{0.15cm}{\rm d}p = \left [ - {\rm e}^{ -{p}/(2\sigma^2)}\hspace{0.15cm} \right ]_{0.5}^{2} ={\rm e}^{-0.25}- {\rm e}^{-1} \approx 0.779 - 0.368 \hspace{0.15cm} \underline{ = 0.411} \hspace{0.05cm}.$$