Exercise 1.3Z: Rayleigh Fading Revisited

Zwei Kanäle, gekennzeichnet durch komplexen Faktor $z(t)$

The graph shows the multiplicative factor $z(t) = x(t) + {\rm j} \cdot y(t)$ of two mobile radio channels (both without multipath propagation) in 2D–representation. The following is assumed:

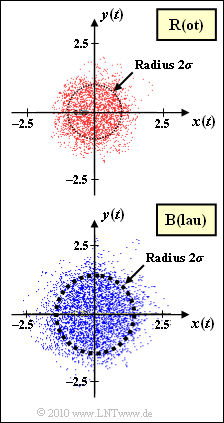
The channel $\rm R$ (the designation results from the color „Red” of the point cloud) is Rayleigh distributed with $\sigma_{\rm R} = 0.5$.
The probability density functions (PDF) of the magnitude $a(t) = |z(t)|$ or the squared magnitude $p(t) = |z(t)|^2$ are $($with $\sigma = \sigma_{\rm R})$:

$$f_a(a) = \left\{ \begin{array}{c} a/\sigma^2 \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} a \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} a < 0 \\ \end{array} \hspace{0.05cm},$$

$$f_p(p) = \left\{ \begin{array}{c} 1/(2\sigma^2) \cdot {\rm e}^{ -{p}/(2\sigma^2)} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r}\hspace{0.15cm} p \ge 0 \\ {\rm f\ddot{u}r}\hspace{0.15cm} p < 0 \\ \end{array} .$$

For channel $\rm B$ ("Blue") only the point cloud is given. It must be estimated whether Rayleigh fading is also present here, and if YES, how large the parameter $\sigma = \sigma_{\rm B}$ is for this channel.
Finally, subtask (3) also refers to PDF $f_{\it \phi}(\phi)$ of the phase function $\phi(t)$ , which is defined as follows:

$$\phi(t) = \arctan \hspace{0.15cm} \frac{y(t)}{x(t)} \hspace{0.05cm}.$$

Notes:

This task belongs to chapter Wahrscheinlichkeitsdichte des Rayleigh–Fadings of this book.
A similar topic is treated with a different approach in chapter Weitere Verteilungen of the book „Stochastic Signal Theory”.
To check your results you can use the interactive applet WDF, VTF and Moments of the book „Stochastic Signal Theory”.

Questionnaire

Sample solution

Musterlösung

(1) YES:

You can see the rotational symmetry here, too, if you consider that only $N = 10\hspace{0.05cm}000$ samples were displayed in the complex plane.
Furthermore the following questions would not make sense if you answer NO.

(2) By measuring the two drawn circles you can see that for the „blue” channel the scattering of real– and imaginary part are larger by a factor of about 1.4 (exactly: $\sqrt{2}$) than for the „red” channel: $$\sigma_{\rm B} = \sigma_{\rm R} \cdot \sqrt{2} = 0.5 \cdot \sqrt{2}= {1}/{\sqrt{2}}\hspace{0.15cm} \underline{\approx 0.707} \hspace{0.05cm}.$$

(3) correct is NO:

In both cases $f_{\it \phi}(\phi)$ describes an equal distribution between $-\pi$ and $+\pi$.
The larger amplitudes of channel $\rm B$ are not important for the phase function $\phi(t)$.

(4) Correct is the solution 2:

With Rayleigh–Fading, the real part $x(t)$ and the imaginary part $y(t)$ are each Gaussian distributed.
The exponential distribution results for the square of the absolute value $p(t) = |z(t)|^2$.

(5) Correct here is the solution 3, as already explained in the sample solution for (4).

(6) The amount $a(t)$ is rayleigh distributed. Therefore, the following applies for the searched probability: $${\rm Pr}(a > A) = \int_{A}^{\infty}\frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.15cm}{\rm d}a \hspace{0.05cm}.$ *In some formula collections you can find the solution for this integral, but not in all. *But it is also valid with the one-sided–exponentially distributed random variable $p = a^2$: $${\rm Pr}(a > A) = {\rm Pr}(p > A^2) = \frac{1}{2\sigma^2} \cdot\int_{A^2}^{\infty} {\rm e}^{ -{p}/(2\sigma^2)} \hspace{0.15cm}{\rm d}p \hspace{0.05cm}.$$ *This integral is elementary and gives the result: $${\rm Pr}(a > A) = {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$ Correct is therefore the <u>solution 2</u>. '''(7)''' For the channel $\rm R$ applies with $\sigma = 0.5$: $${\rm Pr}(|z(t)| > 1) = {\rm e}^{-2} \hspace{0.15cm} \underline{\approx 0.135}

\hspace{0.05cm}.$$

In the upper graph this corresponds to the number of all points outside the circle drawn, based on the number $N = $10,000$ of all points. *For the channel $\rm B$ because of the double variance $\sigma^2 = 0.5$, ${\rm Pr}(|z(t)|>1) = {\rm e}^{\rm –1} applies. \ \underline {\approx \ 0.368}$. *The (not drawn) reference circle would also have the radius 1 in the lower graph. *The circle drawn in the lower graphic has a larger radius than $A = $1, namely $A = \sqrt{2}\approx $1,414.

	The amount $a(t)$ is Gaussian distributed.
	The amount $a(t)$ is Rayleigh distributed.
	The amount $a(t)$ is positive and exponentially distributed.

	The amount $p(t)$ is Gaussian distributed.
	The amount $p(t)$ is Rayleigh distributed.
	The amount $p(t)$ is positive and exponentially distributed.

	${\rm Pr}(\|z(t)\|) > A) = {\rm ln}(A/\sigma).$
	${\rm Pr}(\|z(t)\|) > A) = {\rm e}^{-A^2/2\sigma^2}.$
	${\rm Pr}(\|z(t)\|) > A) = {\rm e}^{-A/\sigma}.$

	Yes.
	No.

	Yes.
	No.