Anwendung auf die Digitalsignalübertragung
Inhaltsverzeichnis
- 1 Informationstheoretisches Modell der Digitalsignalübertragung
- 2 Gerichtetes Schaubild für die Digitalsignalübertragung
- 3 Transinformationsberechnung für den Binärkanal
- 4 Definition und Bedeutung der Kanalkapazität
- 5 Kanalkapazität eines Binärkanals
- 6 Eigenschaften symmetrischer Kanäle
- 7 Einige Grundlagen der Kanalcodierung
- 8 Zusammenhang zwischen Blockfehlern und Bitfehlern
- 9 Rate, Kanalkapazität und Bitfehlerwahrscheinlichkeit
- 10 Aufgaben zum Kapitel
- 11 Quellenverzeichnis
Informationstheoretisches Modell der Digitalsignalübertragung
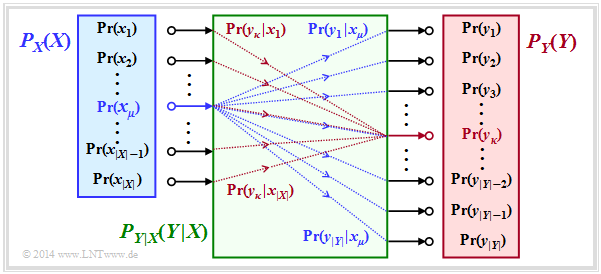
Die bisher allgemein definierten Entropien werden nun auf die Digitalsignalübertragung angewendet, wobei wir von einem digitalen Kanalmodell ohne Gedächtnis (englisch: "Discrete Memoryless Channel", DMC) entsprechend der Grafik ausgehen:
- Die Menge der Quellensymbole wird durch die diskrete Zufallsgröße $X$ charakterisiert, wobei $|X|$ den Quellensymbolumfang angibt:
- $$X = \{\hspace{0.05cm}x_1\hspace{0.05cm}, \hspace{0.15cm} x_2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} x_{\mu}\hspace{0.05cm}, \hspace{0.15cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} x_{|X|}\hspace{0.05cm}\}\hspace{0.05cm}.$$
- Entsprechend kennzeichnet $Y$ die Menge der Sinkensymbole mit dem Symbolumfang $|Y|$:
- $$Y = \{\hspace{0.05cm}y_1\hspace{0.05cm}, \hspace{0.15cm} y_2\hspace{0.05cm},\hspace{0.15cm} \text{...}\hspace{0.1cm} ,\hspace{0.15cm} y_{\kappa}\hspace{0.05cm}, \hspace{0.15cm}\text{...}\hspace{0.1cm} , \hspace{0.15cm} Y_{|Y|}\hspace{0.05cm}\}\hspace{0.05cm}.$$
- Meist gilt $|Y| = |X|$. Möglich ist auch $|Y| > |X|$, zum Beispiel beim Binary Erasure Channel (BEC) mit
- $$X = \{0,\ 1\},\hspace{0.5cm} Y = \{0,\ 1,\ \ \text{E}\}\ ⇒ \ |X| = 2, \ |Y| = 3.$$
- Das Sinkensymbol $\rm E$ kennzeichnet eine Auslöschung (englisch: "Erasure"). Das Ereignis $Y=\text{E}$ gibt an, dass eine Entscheidung für $0$ oder für $1$ zu unsicher wäre.
- Die Symbolwahrscheinlichkeiten der Quelle und der Sinke sind in der Grafik durch die Wahrscheinlichkeitsfunktionen $P_X(X)$ und $P_Y(Y)$ berücksichtigt, wobei gilt:
- $$P_X(x_{\mu}) = {\rm Pr}( X = x_{\mu})\hspace{0.05cm}, \hspace{0.3cm} P_Y(y_{\kappa}) = {\rm Pr}( Y = y_{\kappa})\hspace{0.05cm}.$$
- Es gelte: $P_X(X)$ und $P_Y(Y)$ enthalten keine Nullen ⇒ $\text{supp}(P_X) = P_X$ und $\text{supp}(P_Y) = P_Y$. Diese Voraussetzung erleichtert ohne Verlust der Allgemeingültigkeit die Modellbeschreibung.
- Alle Übergangswahrscheinlichkeiten des digitalen gedächtnislosen Kanals $\rm (DMC)$ werden durch die „bedingte Wahrscheinlichkeitsfunktion” $P_{Y|X}(Y|X)$ erfasst.
Mit $x_μ ∈ X$ und $y_κ ∈ Y$ gelte hierfür folgende Definition:
- $$P_{Y\hspace{0.01cm}|\hspace{0.01cm}X}(y_{\kappa}\hspace{0.01cm} |\hspace{0.01cm} x_{\mu}) = {\rm Pr}(Y\hspace{-0.1cm} = y_{\kappa}\hspace{0.03cm} | \hspace{0.03cm}X \hspace{-0.1cm}= x_{\mu})\hspace{0.05cm}.$$
- Der grüne Block in der Grafik kennzeichnet $P_{Y|X}(⋅)$ mit $|X|$ Eingängen und $|Y|$ Ausgängen. Blaue Verbindungen markieren Übergangswahrscheinlichkeiten $\text{Pr}(y_i | x_μ)$ ausgehend von $x_μ$ mit $1 ≤ i ≤ |Y|$, während alle roten Verbindungen bei $y_κ$ enden: $\text{Pr}(y_κ | x_i)$ mit $1 ≤ i ≤ |X|$.
Bevor wir die Entropien für die einzelnen Wahrscheinlichkeitsfunktionen angeben, nämlich
- $$P_X(X) ⇒ H(X),\hspace{0.5cm} P_Y(Y) ⇒ H(Y), \hspace{0.5cm} P_{XY}(X) ⇒ H(XY), \hspace{0.5cm} P_{Y|X}(Y|X) ⇒ H(Y|X),\hspace{0.5cm} P_{X|Y}(X|Y) ⇒ H(X|Y),$$
sollen die obigen Aussagen an einem Beispiel verdeutlicht werden.
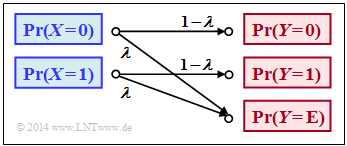
$\text{Beispiel 1}$: Im Buch „Kanalcodierung” behandeln wir auch den Binary Erasure Channel $\rm (BEC)$, der rechts in etwas modifizierter Form skizziert ist. Dabei gelten folgende Voraussetzungen:
- Das Eingangsalphabet sei binär ⇒ $X = \{0,\ 1 \}$ ⇒ $\vert X\vert = 2$, während am Ausgang drei Werte möglich sind ⇒ $Y = \{0,\ 1,\ \text{E} \}$ ⇒ $\vert Y\vert = 3$.
- $\text{E}$ kennzeichnet den Fall, dass sich der Empfänger aufgrund sehr großer Kanalstörungen nicht für eines der Binärsymbole $0$ oder $1$ entscheiden kann. "E" steht hierbei für "Erasure" (Auslöschung).
- Beim $\rm BEC$ werden sowohl eine gesendete $0$ als auch eine $1$ mit der Wahrscheinlichkeit $λ$ ausgelöscht, während die Wahrscheinlichkeit einer richtigen Übertragung jeweils $1 – λ$ beträgt.
- Dagegen werden Übertragungsfehler (Symbolverfälschungen) durch das BEC–Modell ausgeschlossen
⇒ die bedingten Wahrscheinlichkeiten $\text{Pr}(Y = 1 \vert X = 0)$ sowie $\text{Pr}(Y = 0 \vert X = 1)$ sind jeweils Null.
Beim Sender seien die Nullen und Einsen nicht unbedingt gleichwahrscheinlich. Vielmehr verwenden wir die Wahrscheinlichkeitsfunktionen
- $$\begin{align*}P_X(X) & = \big ( {\rm Pr}( X = 0)\hspace{0.05cm},\hspace{0.2cm} {\rm Pr}( X = 1) \big )\hspace{0.05cm},\\ P_Y(Y) & = \big ( {\rm Pr}( Y = 0)\hspace{0.05cm},\hspace{0.2cm} {\rm Pr}( Y = 1)\hspace{0.05cm},\hspace{0.2cm} {\rm Pr}( Y = {\rm E}) \big )\hspace{0.05cm}.\end{align*}$$
Aus obigem Modell erhalten wir dann:
- $$\begin{align*}P_Y(0) & = {\rm Pr}( Y \hspace{-0.1cm} = 0) = P_X(0) \cdot ( 1 - \lambda)\hspace{0.05cm}, \\ P_Y(1) & = {\rm Pr}( Y \hspace{-0.1cm} = 1) = P_X(1) \cdot ( 1 - \lambda)\hspace{0.05cm}, \\ P_Y({\rm E}) & = {\rm Pr}( Y \hspace{-0.1cm} = {\rm E}) = P_X(0) \cdot \lambda \hspace{0.1cm}+\hspace{0.1cm} P_X(1) \cdot \lambda \hspace{0.05cm}.\end{align*}$$
Fassen wir nun $P_X(X)$ und $P_Y(Y)$ als Vektoren auf, so lässt sich das Ergebnis wie folgt darstellen:
- $$P_{\hspace{0.05cm}Y}(Y) = P_X(X) \cdot P_{\hspace{0.05cm}Y\hspace{-0.01cm}\vert \hspace{-0.01cm}X}(Y\hspace{-0.01cm} \vert \hspace{-0.01cm} X) \hspace{0.05cm},$$
wobei die Übergangswahrscheinlichkeiten $\text{Pr}(y_κ\vert x_μ)$ durch folgende Matrix berücksichtigt sind:
- $$P_{\hspace{0.05cm}Y\hspace{-0.01cm} \vert \hspace{-0.01cm}X}(Y\hspace{-0.01cm} \vert \hspace{-0.01cm} X) = \begin{pmatrix} 1 - \lambda & 0 & \lambda\\ 0 & 1 - \lambda & \lambda \end{pmatrix}\hspace{0.05cm}.$$
Beachten Sie bitte:
- Wir haben diese Darstellung nur gewählt, um die Beschreibung zu vereinfachen.
- $P_X(X)$ und $P_Y(Y)$ sind im eigentlichen Sinne keine Vektoren und $P_{Y \vert X}(Y\vert X)$ ist auch keine Matrix.
Gerichtetes Schaubild für die Digitalsignalübertragung
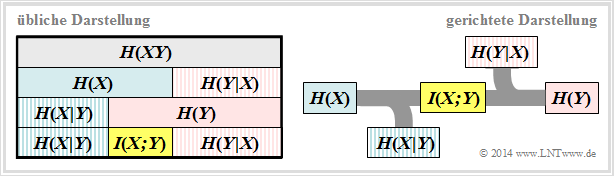
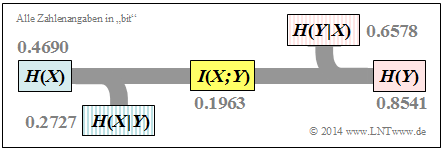
Alle im letzten Kapitel definierten Entropien gelten auch für die Digitalsignalübertragung. Es ist aber zweckmäßig, anstelle des bisher verwendeten Schaubildes entsprechend der linken Grafik die rechte Darstellung zu wählen, bei der die Richtung von der Quelle $X$ zur Sinke $Y$ erkennbar ist.
Interpretieren wir nun ausgehend vom allgemeinen DMC–Kanalmodell die rechte Grafik:
- Die Quellenentropie (englisch: "Source Entropy" ) $H(X)$ bezeichnet den mittleren Informationsgehalt der Quellensymbolfolge. Mit dem Symbolumfang $|X|$ gilt:
- $$H(X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(X)}\right ] \hspace{0.1cm} = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_X(X)}\big ] \hspace{0.2cm} =\hspace{0.2cm} \sum_{\mu = 1}^{|X|} P_X(x_{\mu}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}.$$
- Die Äquivokation (auch „Rückschlussentropie” genannt, englisch: "Equivocation" ) $H(X|Y)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Sinke $Y$ genau Bescheid weiß, durch Beobachtung der Quelle $X$ gewinnt:
- $$H(X|Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{-0.01cm}Y}(X\hspace{-0.01cm} |\hspace{0.03cm} Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{0.03cm}Y} (\hspace{0.05cm}x_{\mu}\hspace{0.03cm} |\hspace{0.05cm} y_{\kappa})} \hspace{0.05cm}.$$
- Die Äquivokation ist der Anteil der Quellenentropie $H(X)$, der durch Kanalstörungen (bei digitalem Kanal: Übertragungsfehler) verloren geht. Es verbleibt die Transinformation (englisch: "Mutual Information") $I(X; Y)$, die zur Sinke gelangt:
- $$I(X;Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)}{P_X(X) \cdot P_Y(Y)}\right ] \hspace{0.2cm} = H(X) - H(X|Y) \hspace{0.05cm}.$$
- Die Irrelevanz (manchmal auch „Streuentropie” genannt, englisch: "Irrelevance") $H(Y|X)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Quelle $X$ genau Bescheid weiß, durch Beobachtung der Sinke $Y$ gewinnt:
- $$H(Y|X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{0.03cm} X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})} \hspace{0.05cm}.$$
- Die Sinkenentropie $H(Y)$ ist der mittlere Informationsgehalt der Sinke. Diese ergibt sich aus der Summe aus der nützlichen Transinformation $I(X; Y)$ und der unnützen Irrelevanz $H(Y|X)$, die ausschließlich von Kanalfehlern herrührt:
- $$H(Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_Y(Y)}\right ] \hspace{0.1cm} = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_Y(Y)}\big ] \hspace{0.2cm} =I(X;Y) + H(Y|X) \hspace{0.05cm}.$$
Transinformationsberechnung für den Binärkanal
Diese Definitionen sollen nun an einem Beispiel verdeutlicht werden. Wir vermeiden bewusst, die Berechnungen durch Ausnutzung von Symmetrien zu vereinfachen.
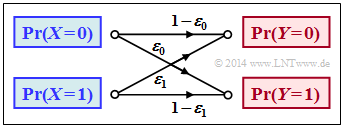
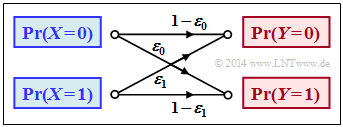
$\text{Beispiel 2}$: Wir betrachten den allgemeinen Binärkanal (englisch: "Binary Channel") ohne Gedächtnis gemäß der Skizze. Die Verfälschungswahrscheinlichkeiten seien:
- $$\begin{align*}\varepsilon_0 & = {\rm Pr}(Y\hspace{-0.1cm} = 1\hspace{0.05cm}\vert X \hspace{-0.1cm}= 0) = 0.01\hspace{0.05cm},\\ \varepsilon_1 & = {\rm Pr}(Y\hspace{-0.1cm} = 0\hspace{0.05cm} \vert X \hspace{-0.1cm}= 1) = 0.2\hspace{0.05cm}\end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{\hspace{0.05cm}Y\hspace{-0.01cm} \vert \hspace{-0.01cm}X}(Y\hspace{-0.01cm} \vert \hspace{-0.01cm} X) = \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} = \begin{pmatrix} 0.99 & 0.01\\ 0.2 & 0.8 \end{pmatrix} \hspace{0.05cm}.$$
Außerdem gehen wir von nicht gleichwahrscheinlichen Quellensymbolen aus:
- $$P_X(X) = \big ( p_0,\ p_1 \big )= \big ( 0.1,\ 0.9 \big ) \hspace{0.05cm}.$$
Mit der binären Entropiefunktion $H_{\rm bin}(p)$ erhält man so für die Quellenentropie:
- $$H(X) = H_{\rm bin} (0.1) = 0.4690 \,{\rm bit} \hspace{0.05cm}.$$
Für die Wahrscheinlichkeitsfunktion der Sinke sowie für die Sinkenentropie ergibt sich somit:
- $$P_Y(Y) = \big [ {\rm Pr}( Y\hspace{-0.1cm} = 0)\hspace{0.05cm}, \ {\rm Pr}( Y \hspace{-0.1cm}= 1) \big ] = \big ( p_0\hspace{0.05cm},\ p_1 \big ) \cdot \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} $$
- $$\begin{align*}\Rightarrow \hspace{0.3cm} {\rm Pr}( Y \hspace{-0.1cm}= 0)& = p_0 \cdot (1 - \varepsilon_0) + p_1 \cdot \varepsilon_1 = 0.1 \cdot 0.99 + 0.9 \cdot 0.2 = 0.279\hspace{0.05cm},\\ {\rm Pr}( Y \hspace{-0.1cm}= 1) & = 1 - {\rm Pr}( Y \hspace{-0.1cm}= 0) = 0.721\end{align*}$$
- $$\Rightarrow \hspace{0.2cm} H(Y) = H_{\rm bin} (0.279) = 0.8541 \,{\rm bit} \hspace{0.05cm}. $$
Die Verbundwahrscheinlichkeiten $p_{\mu \kappa} = \text{Pr}\big[(X = μ) ∩ (Y = κ)\big]$ zwischen Quelle und Sinke sind:
- $$\begin{align*}p_{00} & = p_0 \cdot (1 - \varepsilon_0) = 0.099\hspace{0.05cm},\hspace{0.5cm}p_{01}= p_0 \cdot \varepsilon_0 = 0.001\hspace{0.05cm},\\ p_{10} & = p_1 \cdot (1 - \varepsilon_1) = 0.180\hspace{0.05cm},\hspace{0.5cm}p_{11}= p_1 \cdot \varepsilon_1 = 0.720\hspace{0.05cm}.\end{align*}$$
Daraus erhält man für
- die Verbundentropie (englisch: "Joint Entropy"):
- $$H(XY) = p_{00}\hspace{-0.05cm} \cdot \hspace{-0.05cm}{\rm log}_2 \hspace{0.05cm} \frac{1}{p_{00} \rm } + p_{01} \hspace{-0.05cm} \cdot \hspace{-0.05cm}{\rm log}_2 \hspace{0.05cm} \frac{1}{p_{01} \rm } + p_{10}\hspace{-0.05cm} \cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{1}{p_{10} \rm } + p_{11} \hspace{-0.05cm} \cdot \hspace{-0.05cm} {\rm log}_2\hspace{0.05cm} \frac{1}{p_{11}\rm } = 1.1268\,{\rm bit} \hspace{0.05cm},$$
- die Transinformation (englisch: "Mutual Information"):
- $$I(X;Y) = H(X) + H(Y) - H(XY) = 0.4690 + 0.8541 - 1.1268 = 0.1963\,{\rm bit} \hspace{0.05cm},$$
- die Äquivokation (oder Rückschlussentropie):
- $$H(X \vert Y) \hspace{-0.01cm} =\hspace{-0.01cm} H(X) \hspace{-0.01cm} -\hspace{-0.01cm} I(X;Y) \hspace{-0.01cm} $$
- $$\Rightarrow \hspace{0.3cm} H(X \vert Y) \hspace{-0.01cm} = \hspace{-0.01cm} 0.4690\hspace{-0.01cm} -\hspace{-0.01cm} 0.1963\hspace{-0.01cm} =\hspace{-0.01cm} 0.2727\,{\rm bit} \hspace{0.05cm},$$
- die Irrelevanz (oder Streuentropie):
- $$H(Y \vert X) = H(Y) - I(X;Y) $$
- $$\Rightarrow \hspace{0.3cm} H(Y \vert X) = 0.8541 - 0.1963 = 0.6578\,{\rm bit} \hspace{0.05cm}.$$
Die Ergebnisse sind in der nebenstehenden Grafik zusammengefasst.
Anmerkungen:
- Die Äquivokation und die Irrelevanz hätte man auch direkt (aber mit Mehraufwand) aus den entsprechenden Wahrscheinlichkeitsfunktionen berechnen können.
- Zum Beispiel die Irrelevanz:
- $$H(Y|X) = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.05cm}\in \hspace{0.05cm}XY} \hspace{-0.2cm} P_{XY}(x,\hspace{0.05cm}y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X} (\hspace{0.05cm}y\hspace{0.03cm} |\hspace{0.05cm} x)}= p_{00} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1\hspace{-0.08cm} - \hspace{-0.08cm}\varepsilon_0} + p_{01} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon_0} + p_{10} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1\hspace{-0.08cm} - \hspace{-0.08cm}\varepsilon_1} + p_{11} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon_1} = 0.6578\,{\rm bit} \hspace{0.05cm}.$$
Definition und Bedeutung der Kanalkapazität
Wir betrachten weiter einen diskreten gedächtnislosen Kanal (englisch: Discrete Memoryless Channel, kurz DMC) mit einer endlichen Anzahl an Quellensymbolen ⇒ $|X|$ und ebenfalls nur endlich vielen Sinkensymbolen ⇒ $|Y|$, wie im ersten Abschnitt dieses Kapitels dargestellt.
- Berechnet man die Transinformation $I(X, Y)$ wie zuletzt im $\text{Beispiel 2}$ ausgeführt, so hängt diese auch von der Quellenstatistik ⇒ $P_X(X)$ ab.
- Ergo: Die Transinformation $I(X, Y)$ ist keine reine Kanalkenngröße.
$\text{Definition:}$ Die von Claude E. Shannon eingeführte Kanalkapazität (englisch: Channel Capacity) lautet gemäß seinem Standardwerk [Sha48][1]:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
Da nach dieser Definition stets die bestmögliche Quellenstatistik zugrunde liegt, hängt $C$ nur von den Kanaleigenschaften ⇒ $P_{Y \vert X}(Y \vert X)$ ab, nicht jedoch von der Quellenstatistik ⇒ $P_X(X)$. Oft wird die Zusatzeinheit „bit/Kanalzugriff” hinzugefügt, bei englischen Texten „bit/use”.
Shannon benötigte die Kanalbeschreibungsgröße $C$ zur Formulierung des Kanalcodierungstheorems – eines der Highlights der von ihm begründeten Informationstheorie.
$\text{Shannons Kanalcodierungstheorem:}$
- Zu jedem Übertragungskanal mit der Kanalkapazität $C > 0$ existiert (mindestens) ein $(k, n)$–Blockcode, dessen (Block–)Fehlerwahrscheinlichkeit gegen Null geht, so lange die Coderate $R = k/n$ kleiner oder gleich der Kanalkapazität ist:
- $$R ≤ C.$$
- Voraussetzung hierfür ist allerdings, dass für die Blocklänge dieses Codes gilt:
- $$n → ∞.$$
Den Beweis dieses Theorems, der den Rahmen unseres Lerntutorials sprengen würde, finden Sie zum Beispiel in [CT06][2], [Kra13][3] und [Meck09][4].
Wie in der Aufgabe 3.13 gezeigt werden soll, gilt auch der Umkehrschluss. Auch diesen Beweis finden Sie in den eben genannten Literaturstellen.
$\text{Umkehrschluss von Shannons Kanalcodierungstheorem:}$
Ist die Rate $R$ des verwendeten $(n$, $k)$–Blockcodes größer als die Kanalkapazität $C$, so ist niemals eine beliebig kleine Blockfehlerwahrscheinlichkeit erreichbar.
Im Kapitel AWGN-Modell für zeitdiskrete bandbegrenzte Signale wird im Zusammenhang mit dem wertkontinuierlichen AWGN–Kanalmodell ausgeführt, welche phänomenal große Bedeutung Shannons informationstheoretisches Theorem für die gesamte Informationstechnik besitzt, nicht nur für ausschließlich theoretisch Interessierte, sondern ebenso für Praktiker.
Kanalkapazität eines Binärkanals
Die Transinformation des allgemeinen (unsymmetrischen) Binärkanals gemäß dieser Skizze wurde im $\text{Beispiel 2}$ berechnet. Bei diesem Modell werden die Eingangssymbole $0$ und $1$ unterschiedlich stark verfälscht:
- $$P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{-0.01cm} X) = \begin{pmatrix} 1 - \varepsilon_0 & \varepsilon_0\\ \varepsilon_1 & 1 - \varepsilon_1 \end{pmatrix} \hspace{0.05cm}.$$
Die Transinformation lässt sich mit der Wahrscheinlichkeitsfunktion $P_X(X) = (p_0,\ p_1)$ wie folgt darstellen:
- $$I(X ;Y) = \sum_{\mu = 1}^{2} \hspace{0.1cm}\sum_{\kappa = 1}^{2} \hspace{0.2cm} {\rm Pr} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu}) \cdot {\rm Pr} (\hspace{0.05cm}x_{\mu}\hspace{0.05cm})\cdot {\rm log}_2 \hspace{0.1cm} \frac{{\rm Pr} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})}{{\rm Pr} (\hspace{0.05cm}y_{\kappa})} $$
- $$\begin{align*}\Rightarrow \hspace{0.3cm} I(X ;Y) &= \hspace{-0.01cm} (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0}{(1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 + \varepsilon_1 \cdot p_1} + \varepsilon_0 \cdot p_0 \cdot {\rm log}_2 \hspace{0.1cm} \frac{\varepsilon_0}{(1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_0) \cdot p_0 + \varepsilon_1 \cdot p_1} + \\ & + \hspace{-0.01cm} \varepsilon_1 \cdot p_1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{\varepsilon_1}{\varepsilon_0 \cdot p_0 + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1} + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1}{\varepsilon_0 \cdot p_0 + (1 \hspace{-0.08cm}- \hspace{-0.08cm}\varepsilon_1) \cdot p_1} \hspace{0.05cm}.\end{align*}$$
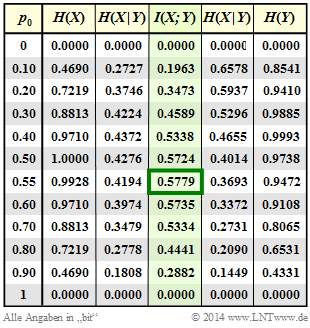
$\text{Beispiel 3}$: Im Folgenden setzen wir $ε_0 = 0.01$ und $ε_1 = 0.2$.
In der Spalte 4 nebenstehender Tabelle ist (grün hinterlegt) die Transinformation $I(X; Y)$ dieses unsymmetrischen Binärkanals abhängig von der Quellensymbolwahrscheinlichkeit $p_0 = {\rm Pr}(X = 0)$ angegeben. Man erkennt:
- Die Transinformation hängt von den Symbolwahrscheinlichkeiten $p_0$ und $p_1 = 1 - p_0$ ab.
- Der Maximalwert von $I(X; Y)$ ergibt sich hier zu $p_0 ≈ 0.55$ ⇒ $p_1 ≈ 0.45$.
- Das Ergebnis $p_0 > p_1$ folgt aus der Relation $ε_0 < ε_1$ (die Null wird weniger verfälscht).
- Die Kapazität dieses Kanals ist $C = 0.5779 \ \rm bit/Kanalzugriff$.
In obiger Gleichung ist als Sonderfall auch der Binary Symmetric Channel $\rm (BSC)$ mit den Parametern $ε = ε_0 = ε_1$ mitenthalten. Hinweise:
- In Aufgabe 3.10 wird die Transinformation des BSC–Kanals für die Systemparameter $ε = 0.1$ und $p_0 = 0.2$ berechnet.
- In der Aufgabe 3.10Z wird dessen Kanalkapazität wie folgt angegeben:
- $$C_{\rm BSC} = 1 - H_{\rm bin} (\varepsilon) \hspace{0.05cm}.$$
Eigenschaften symmetrischer Kanäle
Die Kapazitätsberechnung des (allgemeinen) diskreten gedächtnislosen Kanals ist oftmals aufwändig. Sie vereinfacht sich entscheidend, wenn Symmetrien des Kanals ausgenutzt werden.
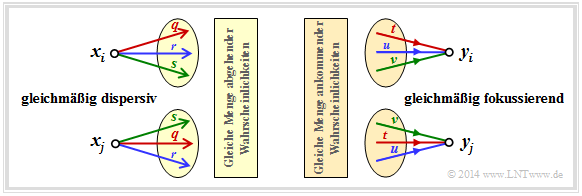
Die Grafik zeigt zwei Beispiele:
- Beim gleichmäßig dispersiven Kanal (englisch: Uniformly Dispersive Channel ) ergibt sich für alle Quellensymbole $x ∈ X$ die genau gleiche Menge an Übergangswahrscheinlichkeiten ⇒ $\{P_{Y\hspace{0.03cm}|\hspace{0.01cm}X}(y_κ\hspace{0.05cm}|\hspace{0.05cm}x)\}$ mit $1 ≤ κ ≤ |Y|$. Für die Werte $q$, $r$, $s$ muss hier stets $q + r + s = 1$ gelten (linke Grafik).
- Beim gleichmäßig fokussierenden Kanal (englisch: Uniformely Focusing Channel ) ergibt sich für alle Sinkensymbole $y ∈ Y$ die gleiche Menge an Übergangswahrscheinlichkeiten ⇒ $\{P_{Y\hspace{0.03cm}|\hspace{0.01cm}X}(y\hspace{0.05cm}|\hspace{0.05cm}x_μ)\}$ mit $1 ≤ μ ≤ |X|$. Hier muss nicht notwendigerweise $t + u + v = 1$ gelten (rechte Grafik).
$\text{Definition:}$ Ist ein diskreter gedächtnisloser Kanal sowohl gleichmäßig dispersiv als auch gleichmäßig fokussierend, so liegt ein streng symmetrischer Kanal (englisch: Strongly Symmetric Channel ) vor. Bei gleichverteiltem Quellenalphabet besitzt dieser die Kapazität
- $$C = {\rm log}_2 \hspace{0.1cm} \vert Y \vert + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{\hspace{0.03cm}Y \vert \hspace{0.01cm} X}(y\hspace{0.05cm} \vert \hspace{0.05cm}x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \vert \hspace{0.01cm} X}(y\hspace{0.05cm}\vert\hspace{0.05cm} x) \hspace{0.05cm}.$$
Für diese Gleichung kann jedes beliebige $x ∈ X$ herangezogen werden.
Diese Definition soll nun durch ein Beispiel verdeutlicht werden.
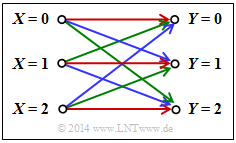
$\text{Beispiel 4}$: Beim betrachteten Kanal gibt es Verbindungen zwischen allen $ \vert X \vert = 3$ Eingängen und allen $ \vert Y \vert = 3$ Ausgängen:
- Eine rote Verbindung steht für $P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm} \vert \hspace{0.05cm} x_μ) = 0.7$.
- Eine blaue Verbindung steht für $P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert \hspace{0.05cm} x_μ) = 0.2$.
- Eine grüne Verbindung steht für $P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert\hspace{0.05cm} x_μ) = 0.1$.
Nach obiger Gleichung gilt dann für die Kanalkapazität:
- $$C = {\rm log}_2 \hspace{0.1cm} (3) + 0.7 \cdot {\rm log}_2 \hspace{0.1cm} (0.7) + 0.2 \cdot {\rm log}_2 \hspace{0.1cm} (0.2) + 0.1 \cdot {\rm log}_2 \hspace{0.1cm} (0.1) = 0.4282 \,\,{\rm bit} \hspace{0.05cm}.$$
Hinweise:
- Der Zusatz „die gleiche Menge an Übergangswahrscheinlichkeiten” bedeutet nicht, dass $P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert\hspace{0.05cm} x_1) = P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert\hspace{0.05cm} x_2) = P_{Y \hspace{0.03cm}\vert\hspace{0.01cm} X}(y_κ \hspace{0.05cm}\vert\hspace{0.05cm} x_3)$ gelten muss.
- Vielmehr geht hier von jedem Eingang ein roter, ein blauer und ein grüner Pfeil ab und an jedem Ausgang kommt ein roter, ein blauer und ein grüner Pfeil an.
- Die jeweiligen Reihenfolgen permutieren: R – G – B, B – R – G, G – B – R.
Ein Beispiel für einen streng symmetrischen Kanal ist der Binary Symmetric Channel $\rm (BSC)$. Dagegen ist der Binary Erasure Channel $\rm (BEC)$ nicht streng symmetrisch,
- da er zwar gleichmäßig dispersiv ist,
- aber nicht gleichmäßig fokussierend.
Die nachfolgende Definition ist weniger restriktiv als die vorherige des streng symmetrischen Kanals.
$\text{Definition:}$ Ein symmetrischer Kanal (englisch: Symmetric Channel ) liegt vor,
- wenn er in mehrere $($allgemein $L)$ streng symmetrische Teilkanäle aufgeteilt werden kann,
- indem das Ausgangsalphabet $Y$ in $L$ Teilmengen $Y_1$, ... , $Y_L$ aufgespalten wird.
Ein solcher symmetrischer Kanal besitzt die folgende Kapazität:
- $$C = \sum_{l \hspace{0.05cm}=\hspace{0.05cm} 1}^{L} \hspace{0.1cm} p_{\hspace{0.03cm}l} \cdot C_{\hspace{0.03cm}l} \hspace{0.05cm}.$$
Hierbei sind folgende Bezeichnungen verwendet:
- $p_{\hspace{0.03cm}l}$ gibt die Wahrscheinlichkeit an, dass der $l$–te Teilkanal ausgewählt wird,
- $C_{\hspace{0.03cm}l}$ ist die Kanalkapazität dieses $l$–ten Teilkanals.
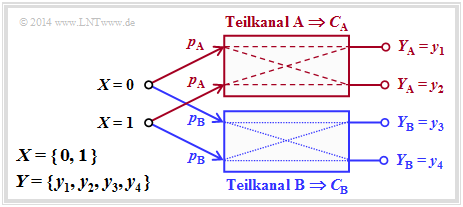
Die Grafik verdeutlicht diese Definition für $L = 2$, wobei die Teilkanäle mit $\rm A$ und $\rm B$ bezeichnet sind.
- An den unterschiedlich gezeichneten Übergängen (gestrichelt oder gepunktet) erkennt man, dass die zwei Teilkanäle verschieden sein können, so dass allgemein $C_{\rm A} ≠ C_{\rm B}$ gelten wird.
- Für die Kapazität des Gesamtkanals erhält man somit allgemein:
- $$C = p_{\rm A} \cdot C_{\rm A} + p_{\rm B} \cdot C_{\rm B} \hspace{0.05cm}.$$
- Über die Struktur der beiden Teilkanäle wird hier keine Aussage gemacht.
Im folgenden Beispiel wird sich zeigen, dass auch der Binary Erasure Channel $\rm (BEC)$ durch diese Grafik grundsätzlich beschreibbar ist. Allerdings müssen dann die zwei Ausgangssysmbole $y_3$ und $y_4$ zu einem einzigen Symbol zusammengefasst werden.
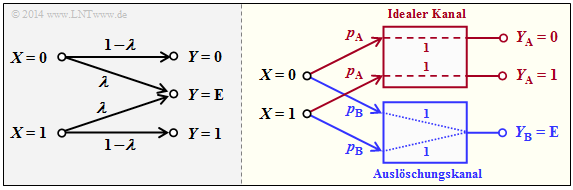
$\text{Beispiel 5}$: Die linke Grafik zeigt die übliche Darstellung des Binary Erasure Channels $\rm (BEC)$ mit Eingang $X = \{0,\ 1\}$ und Ausgang $Y = \{0,\ 1,\ \text{E} \}$.
Teilt man diesen entsprechend der rechten Grafik auf in
- einen idealen Kanal $(y = x)$ für
- $$y ∈ Y_{\rm A} = \{0, 1\} \ \ ⇒ \ \ C_{\rm A} = 1 \ \rm bit/use,$$
- einen Auslöschungskanal für
- $$y ∈ Y_{\rm B} = \{\rm E \} \ \ ⇒ \ \ C_{\rm B} = 0,$$
so ergibt sich mit den Teilkanalgewichtungen $p_{\rm A} = 1 – λ$ und $p_{\rm B} = λ$ für die Kanalkapazität:
- $$C_{\rm BEC} = p_{\rm A} \cdot C_{\rm A} = 1 - \lambda \hspace{0.05cm}.$$
Beide Kanäle sind streng symmetrisch. Für den (idealen) Kanal $\rm A$ gilt gleichermaßen
- für $X = 0$ und $X = 1$: $\text{Pr}(Y = 0 \hspace{0.05cm}\vert \hspace{0.05cm} X) = \text{Pr}(Y = 1 \hspace{0.05cm} \vert\hspace{0.05cm} X) = 1 - λ$ ⇒ gleichmäßig dispersiv,
- für $Y = 0$ und $Y = 1$: $\text{Pr}(Y \hspace{0.05cm} \vert \hspace{0.05cm} X= 0) = Pr(Y \hspace{0.05cm}\vert\hspace{0.05cm} X = 1) = 1 - λ$ ⇒ gleichmäßig fokussierend.
Entsprechendes gilt für den Auslöschungskanal $\rm B$.
In der Aufgabe 3.12 wird sich zeigen, dass die Kapazität des Kanalmodells Binary Symmetric Error & Erasure Channel $\rm (BSEC)$ in gleicher Weise berechnet werden kann. Man erhält:
- $$C_{\rm BSEC} = (1- \lambda) \cdot \left [ 1 - H_{\rm bin}(\frac{\varepsilon}{1- \lambda}) \right ]$$
- mit der Verfälschungswahrscheinlichkeit $ε$
- und der Auslöschungswahrscheinlichkeit $λ$.
Einige Grundlagen der Kanalcodierung
Um das Kanalcodierungstheorem richtig interpretieren zu können, sind einige Grundlagen der Kanalcodierung (englisch: Channel Coding) erforderlich. Dieses äußerst wichtige Gebiet der Nachrichtentechnik wird in unserem Lerntutorial $\rm LNTwww$ in einem eigenen Buch namens Kanalcodierung behandelt.
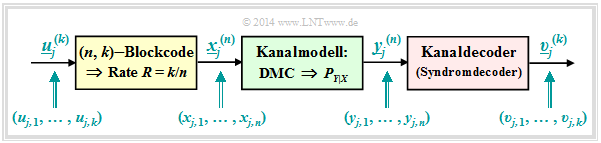
Die folgende Beschreibung bezieht sich auf das stark vereinfachte Modell für binäre Blockcodes:
- Die unendlich lange Quellensymbolfolge $\underline{u}$ (hier nicht dargestellt) wird in Blöcke zu jeweils $k$ Bit unterteilt. Wir bezeichnen den Informationsblock mit der laufenden Nummerierung $j$ mit $\underline{u}_j^{(k)}$.
- Jeder Informationsblock $\underline{u}_j^{(k)}$ wird durch den gelb hinterlegten Kanalcoder in ein Codewort $\underline{x}_j^{(n)}$ umgesetzt, wobei $n > k$ gelten soll. Das Verhältnis $R = k/n$ bezeichnet man als die Coderate.
- Der Discrete Memoryless Channel $\rm (DMC)$ wird durch Übergangswahrscheinlichkeiten $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(⋅)$ berücksichtigt. Dieser grün hinterlegte Block bewirkt Fehler auf Bitebene. Es kann also gelten: $y_{j, \hspace{0.03cm}i} ≠ x_{j,\hspace{0.03cm} i}$.
- Damit können sich auch die aus $n$ Bit bestehenden Empfangsblöcke $\underline{y}_j^{(n)}$ von den Codeworten $\underline{x}_j^{(n)}$ unterscheiden . Ebenso gilt im allgemeinen für die Blöcke nach dem Deoder: $\underline{v}_j^{(k)} ≠ \underline{u}_j^{(k)}$.
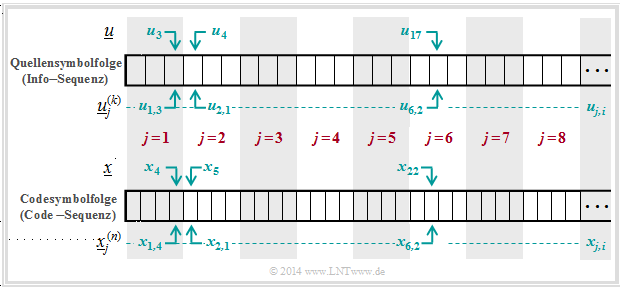
$\text{Beispiel 6}$: Die Grafik soll die hier verwendete Nomenklatur am Beispiel $k = 3$ und $n = 4$ verdeutlichen. Dargestellt sind die jeweils ersten acht Blöcke der Informationssequenz $\underline{u}$ und der Codesequenz $\underline{x}$.
Man erkennt folgende Zuordnung zwischen der geblockten und der ungeblockten Beschreibung:
- Bit 3 des 1. Info–Blocks ⇒ $u_{1,\hspace{0.08cm} 3}$ entspricht dem Symbol $u_3$ in ungeblockter Darstellung.
- Bit 1 des 2. Info–Blocks ⇒ $u_{2, \hspace{0.08cm}1}$ entspricht dem Symbol $u_4$ in ungeblockter Darstellung.
- Bit 2 des 6. Info–Blocks ⇒ $u_{6, \hspace{0.08cm}2}$ entspricht dem Symbol $u_{17}$ in ungeblockter Darstellung.
- Bit 4 des 1. Codewortes ⇒ $x_{1, \hspace{0.08cm}4}$ entspricht dem Symbol $x_4$ in ungeblockter Darstellung.
- Bit 1 des 2. Codewortes ⇒ $x_{2, \hspace{0.08cm}1}$ entspricht dem Symbol $x_5$ in ungeblockter Darstellung.
- Bit 2 des 6. Codewortes ⇒ $x_{6, \hspace{0.08cm}2}$ entspricht dem Symbol $x_{22}$ in ungeblockter Darstellung.
Zusammenhang zwischen Blockfehlern und Bitfehlern
Zur Interpretation des Kanalcodierungstheorems benötigen wir noch verschiedene Definitionen für „Fehlerwahrscheinlichkeiten”. Aus dem obigen Systemmodell lassen sich verschiedene Beschreibungsgrößen ableiten:
$\text{Definitionen:}$
- Die $\rm {Kanalfehlerwahrscheinlichkeit}$ ergibt sich beim vorliegenden Kanalmodell zu
- $${\rm Pr(Kanalfehler)} = {\rm Pr} \left ({y}_{j,\hspace{0.05cm} i} \ne {x}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$
- Beispielsweise ist beim BSC–Modell $\text{Pr(Kanalfehler)} = ε$ für alle $j = 1, 2$, ... und $1 ≤ i ≤ n$.
- Die $\rm {Blockfehlerwahrscheinlichkeit}$ bezieht sich auf die zugeordneten Informationsblöcke am Codereingang ⇒ $\underline{u}_j^{(k)}$ und am Decoderausgang ⇒ $\underline{v}_j^{(k)}$,
jeweils in Blöcken zu $k$ Bit:
- $${\rm Pr(Blockfehler)} = {\rm Pr} \left (\underline{\upsilon}_j^{(k)} \ne \underline{u}_j^{(k)} \right )\hspace{0.05cm}.$$
- Die $\rm {Bitfehlerwahrscheinlichkeit}$ bezieht sich ebenfalls auf den Eingang und den Ausgang des betrachteten Codiersystems, allerdings auf Bitebene:
- $${\rm Pr(Bitfehler)} = {\rm Pr} \left ({\upsilon}_{j,\hspace{0.05cm} i} \ne {u}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$
- Hierbei ist vereinfachend vorausgesetzt, dass alle $k$ Bit $u_{j,\hspace{0.08cm}i}$ des Informationsblockes $j$ mit gleicher Wahrscheinlichkeit verfälscht werden $(1 ≤ i ≤ k)$. Andernfalls müsste über die $k$ Bit noch gemittelt werden.
Zwischen der Blockfehler– und der Bitfehlerwahrscheinlichkeit besteht allgemein der Zusammenhang:
- $$\frac{1}{k} \cdot {\rm Pr(Blockfehler)} \le {\rm Pr(Bitfehler)} \le {\rm Pr(Blockfehler)} \hspace{0.05cm}.$$
- Die untere Schranke ergibt sich, wenn bei allen fehlerhaften Blöcken alle Bit falsch sind.
- Gibt es in jedem fehlerhaften Block genau nur einen einzigen Bitfehler, dann ist die Bitfehlerwahrscheinlichkeit ⇒ ${\rm Pr(Bitfehler)}$ identisch mit der Blockfehlerwahrscheinlichkeit ⇒ ${\rm Pr(Blockfehler)}$.
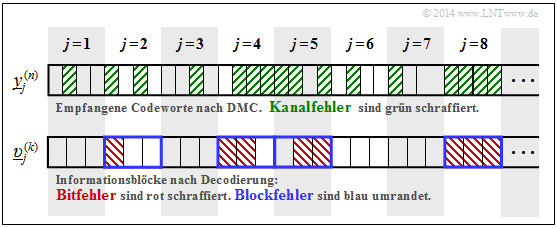
$\text{Beispiel 7:}$ Die Grafik zeigt oben die ersten acht Empfangsblöcke $\underline{y}_j^{(n)}$ mit jeweils $n = 4$ Bit. Kanalfehler sind grün schraffiert.
Unten ist die Ausgangsfolge $\underline{v}$ skizziert, unterteilt in Blöcke $\underline{v}_j^{(k)}$ mit jeweils $k = 3$ Bit:
- Bitfehler sind im unteren Diagramm rot schraffiert.
- Blockfehler erkennt man an der blauen Umrahmung.
Hierzu einige (aufgrund der kurzen Folge) nur sehr vage Angaben zu den Fehlerwahrscheinlichkeiten:
- Die Hälfte der Empfangsbits sind grün schraffiert. Daraus folgt:
- $${\rm Pr(Kanalfehler)} = 16/32 = 1/2.$$
- Die Bitfehlerwahrscheinlichkeit lautet mit der beispielhaften Codierung & Decodierung:
- $${\rm Pr(Bitfehler)} = 8/24 = 1/3.$$
- Dagegen würde bei uncodierter Übertragung gelten:
- $${\rm Pr(Bitfehler)} = {\rm Pr(Kanalfehler)} = 1/2.$$
- Die Hälfte der decodierten Blöcke sind blau umrandet. Daraus folgt:
- $${\rm Pr(Blockfehler)} = 4/8 = 1/2.$$
Mit ${\rm Pr(Blockfehler)}= 1/2$ und $k = 3$ liegt die Bitfehlerwahrscheinlichkeit in folgendem Bereich:
- $$1/6 \le {\rm Pr(Bitfehler)} \le 1/2 \hspace{0.05cm}.$$
- Die obere Schranke bezüglich Bitfehler ergibt sich, wenn in jedem der vier verfälschten Blöcke alle Bit falsch sind: ${\rm Pr(Bitfehler)} = 12/24 = 1/2.$
- Die untere Schranke gibt an, dass in jedem der vier verfälschten Blöcke jeweils nur ein Bit falsch ist: ${\rm Pr(Bitfehler)} = 4/24 = 1/6$.
Rate, Kanalkapazität und Bitfehlerwahrscheinlichkeit
Grundsätzlich gilt:
- Durch Kanalcodierung wird die Zuverlässigkeit (englisch: Reliability) der Datenübertragung von der Quelle zur Sinke erhöht.
- Vermindert man die Coderate $R = k/n$ und erhöht so die hinzugefügte Redundanz $(1 - R)$, so wird im allgemeinen die Datensicherheit verbessert und damit die Bitfehlerwahrscheinlichkeit herabgesetzt, die wir im Weiteren kurz mit $p_{\rm B}$ bezeichnen:
- $$p_{\rm B} = {\rm Pr(Bitfehler)} = {\rm Pr} \left ({\upsilon}_{j,\hspace{0.05cm} i} \ne {u}_{j,\hspace{0.05cm} i} \right )\hspace{0.05cm}.$$
Das folgende Theorem basiert auf dem Data Processing Theorem und Fano's Lemma. Die Herleitung kann in den Standardwerken zur Informationstheorie nachgelesen werden, zum Beispiel in [CT06][2]:
$\text{Umkehrung des Shannonschen Kanalcodierungstheorems:}$
Benutzt man zur Datenübertragung mit Rate $R$ einen Kanal mit zu kleiner Kapazität $C < R$, so kann die Bitfehlerwahrscheinlichkeit $p_{\rm B}$ auch bei bestmöglicher Kanalcodierung eine untere Schranke nicht unterschreiten:
- $$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - {C}/{R}\right ) > 0\hspace{0.05cm}.$$
Hierbei bezeichnet $H_{\rm bin}(⋅)$ die binäre Entropiefunktion.
Da die Wahrscheinlichkeit der Blockfehler nie kleiner sein kann als die der Bitfehler, ist für $R > C$ auch die Blockfehlerwahrscheinlichkeit „Null” nicht möglich.
Aus den angegebenen Schranken für die Bitfehler,
- $$\frac {1}{k} \cdot {\rm Pr}({\rm Blockfehler}) \le {\rm Pr}({\rm Bitfehler}) \le {\rm Pr}({\rm Blockfehler})\hspace{0.05cm},$$
lässt sich auch ein Bereich für die Blockfehlerwahrscheinlichkeit angeben:
- $$ {\rm Pr}({\rm Bitfehler}) \le {\rm Pr}({\rm Blockfehler}) \le k \cdot {\rm Pr}({\rm Bitfehler})\hspace{0.05cm}.$$
$\text{Beispiel 8:}$ Bei einem Kanal mit Kapazität $C = 1/3$ (bit) ist eine fehlerfreie Datenübertragung $(p_{\rm B} = 0)$ mit der Coderate $R < 1/3$ prinzipiell möglich.
- Allerdings ist aus dem Kanalcodierungstheorem der spezielle $(k$, $n)$–Blockcode nicht bekannt, der dieses Wunschergebnis ermöglicht. Auch Shannon macht hierzu keine Aussagen.
- Bekannt ist nur, dass ein solcher bestmöglicher Code mit unendlich langen Blöcken arbeitet. Bei gegebener Coderate $R = k/n$ gilt somit sowohl $k → ∞$ als auch $n → ∞$.
- Deshalb ist die Aussage „Die Bitfehlerwahrscheinlichkeit ist Null” nicht identisch mit „Es treten keine Bitfehler auf”: Auch bei endlich vielen Bitfehlern und $k → ∞$ gilt nämlich $p_{\rm B} = 0$.
Mit der Coderate $R = 1 > C$ (uncodierte Übertragung) erhält man:
- $$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - \frac{1/3}{1}\right ) = H_{\rm bin}^{-1}(2/3) \approx 0.174 > 0\hspace{0.05cm}.$$
Mit der Coderate $R = 1/2 > C$ ist die Bitfehlerwahrscheinlichkeit zwar kleiner, aber ebenfalls von Null verschieden:
- $$p_{\rm B} \ge H_{\rm bin}^{-1} \cdot \left ( 1 - \frac{1/3}{1/2}\right ) = H_{\rm bin}^{-1}(1/3) \approx 0.062 > 0\hspace{0.05cm}.$$
Aufgaben zum Kapitel
Aufgabe 3.10: Transinformation beim BSC
Aufgabe 3.10Z: BSC–Kanalkapazität
Aufgabe 3.11: Auslöschungskanal
Aufgabe 3.11Z: Extrem unsymmetrischer Kanal
Aufgabe 3.12: Streng symmetrische Kanäle
Aufgabe 3.13: Coderate und Zuverlässigkeit
Aufgabe 3.14: Kanalcodierungstheorem
Aufgabe 3.15: Data Processing Theorem
Quellenverzeichnis
- ↑ Shannon, C.E.: A Mathematical Theory of Communication. In: Bell Syst. Techn. J. 27 (1948), S. 379-423 und S. 623-656.
- ↑ 2,0 2,1 Cover, T.M.; Thomas, J.A.: Elements of Information Theory. West Sussex: John Wiley & Sons, 2nd Edition, 2006.
- ↑ Kramer, G.: Information Theory. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2013.
- ↑ Mecking, M.: Information Theory. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2009.