Aufgabe 3.3Z: Hoch- und Tiefpässe in p-Form

Betrachtete Vierpolschaltungen

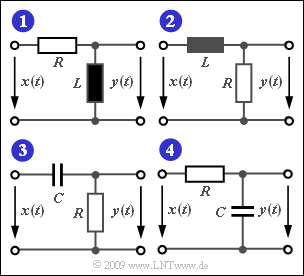
Die Grafik zeigt vier einfache Filterkonfigurationen mit Tiefpass– bzw. Hochpasscharakteristik, die sich aus diskreten Bauelementen zusammensetzen.

Für die Bauelemente der Schaltungen $(1)$ und $(2)$ gelte:

$$R = 100\,{\rm \Omega}\hspace{0.05cm},\hspace{0.2cm} L = 10\,{\rm µ H}\hspace{0.05cm}.$$

Die Vierpol–Schaltungen $(1)$, ... , $(4)$ sollen durch ihre $p$–Übertragungsfunktionen $H_{\rm L}(p)$ charakterisiert werden.
Daraus ergibt sich (bei dieser Aufgabe, nicht allgemein) der Frequenzgang entsprechend der Gleichung

$$H(f) = H_{\rm L}(p)\Bigg |_{\hspace{0.1cm} p\hspace{0.05cm}=\hspace{0.05cm}{\rm j \hspace{0.05cm}2\pi \it f}} \hspace{0.05cm}.$$

Hinweis:

Die Aufgabe gehört zum Kapitel Laplace–Transformation und p–Übertragungsfunktion.

Fragebogen

	Für einen Tiefpass erster Ordnung gilt: $H_{\rm TP}(p) = K/(p + p_{\rm x})$,
	Für einen Hochpass erster Ordnung gilt: $H_{\rm HP}(p) = K \cdot p/(p + p_{\rm x})$.

$K \ = \ $

$p_{\rm x}\ = \ $

$\ \cdot 10^{-6}\ \rm 1/s$

$f_{\rm G} \ = \ $

$\ \rm MHz$

	Vierpol $(3)$,
	Vierpol $(4)$.

$C \ = \ $

$\ \rm nF$

Musterlösung

(1) Beide Aussagen treffen zu:

Für die beiden Vierpole gelten folgende Grenzwerte:

$$\lim_{p \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} H_{\rm TP}(p)\hspace{0.2cm} = \hspace{0.1cm}\lim_{p \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{K}{p + p_{\rm x}} \hspace{0.15cm} { =K /{p_{\rm x}}}, \hspace{1.2cm} \lim_{p \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H_{\rm TP}(p)= 0\hspace{0.05cm},$$

$$ \lim_{p \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}H_{\rm HP}(p) \hspace{0.2cm} = \hspace{0.1cm}0, \hspace{1.4cm} \lim_{p \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} H_{\rm HP}(p)= \lim_{p \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty}\frac{K\cdot p}{p + p_{\rm x}} = K \hspace{0.05cm}.$$

Man erkennt, dass $H_{\rm TP}(p)$ für sehr hohe Frequenzen Null ergibt und $H_{\rm HP}(p)$ für sehr niedrige Frequenzen.

(2) Wir betrachten den Vierpol $(1)$.

Der Spannungsteiler liefert das Ergebnis

$$H_{\rm L}(p)= \frac { p L} {R + pL}= \frac { p } {p +{R}/{L}} \hspace{0.05cm} .$$

Es handelt sich um einen $\rm Hochpass$ mit dem Kennparameter $\underline {K = 1}$ und der Nullstelle bei

$$p_{\rm x}= -\frac{R}{L}= -\frac{100\,{\rm \Omega}}{10^{-5 }\,{\rm \Omega s}}\hspace{0.15cm}\underline{= -0.1} \cdot10^{-6 }\,{1}/{\rm s} \hspace{0.05cm} .$$

(3) Zur Übertragungsfunktion kommt man mit der Substitution $p = {\rm j} \cdot 2 \pi f$:

$$H(f)= \frac { {\rm j} \cdot 2\pi \hspace{-0.05cm}f } {{\rm j} \cdot 2\pi \hspace{-0.05cm}f +p_{\rm x}}\Rightarrow \hspace{0.3cm}\hspace{0.3cm} |H(f)|^2 = \frac { (2\pi \hspace{-0.05cm}f)^2 } {(2\pi \hspace{-0.05cm}f)^2 +p_{\rm x}^2}\hspace{0.05cm} .$$

Aus der Bedingung $|H(f_{\rm G})|^2 = 0.5 $ erhält man folgende Bestimmungsgleichung:

$$(2\pi \hspace{-0.05cm}f_{\rm G})^2 = p_{\rm x}^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\hspace{0.3cm} f_{\rm G} = -\frac { p_{\rm x}} {2 \pi}= \frac { 10^{-7 }\, 1/s} {2 \pi}\hspace{0.15cm}\underline{\approx 1.59\,{\rm MHz}}\hspace{0.05cm} .$$

(4) Richtig ist die erste Aussage:

Für ein Gleichsignal ist eine Kapazität $C$ ein unendlich großer Widerstand, für hohe Frequenzen wirkt $C$ wie ein Kurzschluss.
Daraus folgt: Der Vierpol $(3)$ beschreibt ebenfalls einen Hochpass. Dagegen zeigen die Schaltungen $(2)$ und $(4)$ Tiefpassverhalten.

(5) Die $p$–Übertragungsfunktion von Vierpol $(3)$ lautet:

$$H_{\rm L}(p)= \frac { R } {{1}/{(pC)} + R}= \frac { p } {p +{1}/{(RC)}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm x}= -{1}/(RC)\hspace{0.3cm}\Rightarrow \hspace{0.3cm} C = -\frac{1}{p_{\rm x} \cdot R}= \frac{-1}{-10^{-7 }\, 1/s \cdot 100\,{\rm \Omega}}\hspace{0.15cm}\underline{ = 1\,{\rm nF}} \hspace{0.05cm} .$$