Systembeschreibung im Frequenzbereich

Das Ursachen-Wirkungs-Prinzip

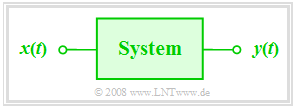
Wir betrachten in diesem Kapitel stets das folgende einfache Modell:

Diese Anordnung ist wie folgt zu interpretieren:

Im Mittelpunkt steht das so genannte System, das in seiner Funktion weitestgehend abstrahiert ist („Black Box”). Über die Realisierung des Systems ist nichts Genaues bekannt.
Die auf dieses System einwirkende zeitabhängige Eingangsgröße x(t) bezeichnen wir im Folgenden auch als die Ursachenfunktion.
Am Ausgang des Systems erscheint dann die Wirkungsfunktion y(t) – quasi als Antwort des Systems auf die Eingangsfunktion x(t).

Anmerkung: Das System kann im Allgemeinen von beliebiger Art sein und ist nicht allein auf die Nachrichtentechnik beschränkt. Vielmehr wird auch in anderen Wissenschaftsgebieten wie zum Beispiel den Naturwissenschaften, der Volks- und Betriebswirtschaft, der Soziologie und Politologie versucht, Kausalzusammenhänge zwischen verschiedenen Größen durch das Ursachen–Wirkungs–Prinzip zu erfassen und zu beschreiben. Die für diese phänomenologischen Systemtheorien angewandten Methoden unterscheiden sich aber deutlich von der Vorgehensweise in der Nachrichtentechnik, die in diesem ersten Kapitel des Buches „Lineare zeitinvariante Systeme” dargelegt wird.

Anwendung in der Nachrichtentechnik

Das Ursachen–Wirkungs–Prinzip lässt sich auch in der Nachrichtentechnik anwenden, beispielsweise zur Beschreibung von Zweipolen. Hier kann man den Stromverlauf i(t) als Ursachen- und die Spannung u(t) als Wirkungsfunktion betrachten. Durch Beobachten der I/U–Beziehungen lassen sich so Rückschlüsse über die Eigenschaften des eigentlich unbekannten Zweipols ziehen.

Karl Küpfmüller hat den Begriff „Systemtheorie” 1949 erstmals (in Deutschland) eingeführt. Er versteht darunter eine Methode zur Beschreibung komplexer Kausalzusammenhänge in Naturwissenschaften und Technik, basierend auf einer Spektraltransformation – beispielsweise der im Buch „Signaldarstellung” dargelegten Fouriertransformation.

Man kann ein ganzes Nachrichtensystem systemtheoretisch beschreiben. Hier ist die Ursachenfunktion das Eingangssignal x(t) bzw. dessen Spektrum X(f) und die Wirkungsfunktion das Ausgangssignal y(t) oder die dazugehörige Spektralfunktion Y(f).

Auch in den nachfolgenden Bildern werden die Eingangsgrößen meist blau, die Ausgangsgrößen rot und Systemgrößen grün gezeichnet.

Beispiel: Beschreibt das „Nachrichtensystem” eine vorgegebene lineare Schaltung, so kann bei bekanntem Eingangssignal x(t) mit Hilfe der Systemtheorie das Ausgangssignal y(t) vorhergesagt werden. Eine zweite Aufgabe der Systemtheorie besteht darin, durch Messung von y(t) bei Kenntnis von x(t) das Nachrichtensystem zu klassifizieren, ohne dieses im Detail zu kennen.

Beschreibt x(t) beispielsweise die Stimme eines Anrufers aus Hamburg und y(t) die Aufzeichnung eines Anrufbeantworters in München, dann besteht das „Nachrichtensystem” aus folgenden Komponenten:

Mikrofon – Telefon – elektrische Leitung – Signalumsetzer – Glasfaserkabel – optischer Verstärker – Signalrücksetzer – Empfangsfilter (Entzerrer, Rauschbegrenzung) – ... – elektromagnetischer Wandler.

Voraussetzungen für die Anwendung der Systemtheorie

Das auf der letzten Seite angegebene Modell eines Nachrichtensystems gilt allgemein und unabhängig von Randbedingungen. Die Anwendung der Systemtheorie erfordert jedoch zusätzlich einige einschränkende Voraussetzungen. Für das Folgende gilt stets, wenn nicht explizit etwas anderes angegeben ist:

Sowohl x(t) als auch y(t) sind deterministische Signale. Andernfalls muss man entsprechend dem Kapitel Stochastische Systemtheorie im Buch „Stochastische Signaltheorie” vorgehen.
Das System ist linear. Dies erkennt man z. B. daran, dass eine harmonische Schwingung x(t) am Eingang auch eine harmonische Schwingung y(t) gleicher Frequenz am Ausgang zur Folge hat:

$$x(t) = A_x \cdot \cos(\omega_0 \hspace{0.05cm}t - \varphi_x)\hspace{0.2cm}\Rightarrow \hspace{0.2cm} y(t) = A_y \cdot\cos(\omega_0 \hspace{0.05cm}t - \varphi_y).$$

Neue Frequenzen entstehen nicht. Lediglich Amplitude und Phase der harmonischen Schwingung können verändert werden. Nichtlineare Systeme werden im Kapitel 2.2 dieses Buches behandelt.
Aufgrund der Linearität ist auch das Superpositionsprinzip anwendbar. Dieses besagt, dass aus $x_1(t) ⇒ y_1(t)$ und $x_2(t) ⇒ y_2(t)$ auch zwingend die folgende Zuordnung gilt:

$$x_1(t) + x_2(t) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y_1(t) + y_2(t)$$.