Systembeschreibung im Zeitbereich

Impulsantwort

Im Kapitel 3 von Buch „Signaldarstellung” wurde dargelegt, dass für jedes deterministische Signal $x(t)$ mit Hilfe der Fouriertransformation eine Spektralfunktion $X(f)$ angegeben werden kann. Oft bezeichnet man $X(f)$ auch kurz als das Spektrum.

Alle Informationen über die Spektralfunktion bleiben auch in der Zeitbereichsdarstellung erhalten, wenn auch nicht immer sofort erkennbar. Der gleiche Sachverhalt trifft für lineare zeitinvariante Systeme zu.

Definition: Die wichtigste Beschreibungsgröße eines linearen zeitinvarianten Systems im Zeitbereich ist die Fourierrücktransformierte von $H(f)$, die man als die Impulsantwort bezeichnet: $$h(t) = \int_{-\infty}^{+\infty}H(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j}2\pi ft}\hspace{0.15cm} {\rm d}f.$$

Hierzu ist Folgendes anzumerken:

Der Frequenzgang $H(f)$ und die Impulsantwort $h(t)$ sind äquivalente Beschreibungsgrößen, die genau die gleichen Informationen über das LZI–System beinhalten.
Verwendet man das diracförmige Eingangssignal $x(t) = δ(t)$, so ist $X(f) = 1$ zu setzen und es gilt $Y(f) = H(f)$ bzw. $y(t) = h(t)$. Die Bezeichnung Impulsantwort spiegelt diese Aussage wieder.
Die obige Definition lässt erkennen, dass jede Impulsantwort die Einheit Hz = $1/s$ besitzen muss.

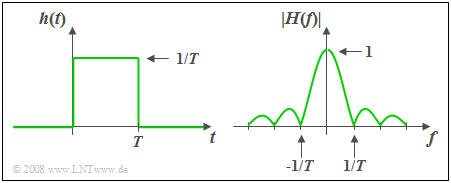
Beispiel: Die Impulsantwort $h(t)$ des so genannten Spalt–Tiefpasses ist über eine Zeitdauer $T$ hinweg konstant und außerhalb dieses Zeitintervalls gleich 0. Der dazugehörige Amplitudengang als der Betrag des Frequenzgangs ist $|H(f)| = |si(πfT)|$. Der Phasenverlauf ergibt sich damit zu $$b(f) = \left\{ \begin{array}{l} \hspace{0.25cm}\pi/T \\ -\pi/T \\ \end{array} \right.\quad \quad\begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{\left| \hspace{0.05cm} f\hspace{0.05cm} \right| > 0,} \\{\left|\hspace{0.05cm} f \hspace{0.05cm} \right|< 0.} \\\end{array}$$ Wäre $h(t)$ symmetrisch um $t$ = 0 und damit akausal, so würde $b(f)$ = 0 gelten.

Die Fläche über die Impulsantwort ist gleich $H(f = 0)$ = 1. Daraus folgt, dass die Impulsantwort im Bereich von 0 bis $T$ gleich $1/T$ sein muss.

Einige Gesetze der Fourier–Transformation

Im Kapitel 3.3 des Buches „Signaldarstellung” wurden die Gesetzmäßigkeiten der Fouriertransformation ausführlich dargelegt. Hier folgt nun eine kurze Zusammenfassung, wobei $H(f)$ den Frequenzgang eines LZI–Systems beschreibt und dessen Fourierrücktransformierte $h(t)$ die Impulsantwort angibt.

Bei allen folgenden Gleichungen wird das Kurzsymbol der Fouriertransformation benutzt. Der ausgefüllte Kreis kennzeichnet stets den Spektralbereich und der weiße Kreis den Zeitbereich.

Multiplikation mit einem konstanten Faktor:

$$k \cdot H(f)\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,k \cdot h(t).$$

Bei $k$ < 1 spricht man von einer Dämpfung, während $k$ > 1 für eine Verstärkung steht.

Ähnlichkeitssatz:

$$H({f}/{k})\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,|k| \cdot h(k\cdot t).$$

Dies besagt: Eine Stauchung ($k$ < 1) des Frequenzgangs führt zu einer breiteren und niedrigeren Impulsantwort. Durch Streckung ($k$ > 1) von $H(f)$ wird $h(t)$ schmaler und höher.

Verschiebungssatz im Frequenz- und Zeitbereich:

$$H(f - f_0) \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, h( t )\cdot {\rm e}^{\hspace{0.05cm}{\rm j}2\pi f_0 t},$$ $$H(f) \cdot {\rm e}^{-{\rm j}2\pi ft_0}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, h( t- t_0 ).$$

Eine Verschiebung um $t_0$ (Laufzeit) führt also im Frequenzbereich zu der Multiplikation mit einer komplexen Exponentialfunktion. Der Amplitudengang $|H(f)|$ wird dadurch nicht verändert.

Differentiationssatz im Frequenz- und Zeitbereich:

$$\frac{1}{{{\rm j}2\pi }} \cdot \frac{{{\rm d}H( f )}}{{{\rm d}f}}\cdot \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,- t \cdot h( t ),$$ $${\rm j}\cdot 2\pi f \cdot H( f ){}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \frac{{{\rm d}h( t )}}{{\rm d}t}.$$

Ein differenzierendes Element im LZI–System führt im Frequenzbereich zu einer Multiplikation mit $j2πf$ und damit unter Anderem zu einer Phasendrehung um 90°.

Diese Gesetzmäßigkeiten werden in den Aufgaben zu den Kapiteln 1.2 und 1.3 häufiger angewendet.