Einige systemtheoretische Tiefpassfunktionen

Allgemeine Bemerkungen

Alle auf den nächsten Seiten beschriebenen Tiefpassfunktionen weisen die folgenden Eigenschaften auf:

Der Frequenzgang $H(f)$ ist stets reell und gerade, so dass nach dem Zuordnungssatz auch die zugehörige Impulsantwort $h(t)$ stets reell und gerade ist.
Damit ist offensichtlich, dass die hier betrachteten Systeme akausal und somit nicht realisierbar sind. Die Beschreibung kausaler Systeme erfolgt im Kapitel 3 dieses Buches.
Der Vorteil dieser systemtheoretischen Filterfunktionen ist die einfache Beschreibung durch maximal zwei Parameter, so dass der Filtereinfluss durchschaubar dargestellt werden kann.
Der wichtigste Funktionsparameter ist die äquivalente Bandbreite entsprechend der Definition über das flächengleiche Rechteck:

$$\Delta f = \frac{1}{H(f=0)}\cdot \int\limits_{-\infty}^{+\infty}H(f) \hspace{0.15cm} {\rm d}f.$$

Nach dem so genannten Reziprozitätsgesetz liegt somit auch die äquivalente Zeitdauer der Impulsantwort fest, die ebenfalls über das flächengleiche Rechteck definiert ist:

$$\Delta t = \frac{1}{h(t=0)}\cdot \int\limits_{-\infty}^{+\infty}h(t) \hspace{0.15cm} {\rm d}t = \frac{1}{\Delta f}.$$

Der Gleichsignalübertragungsfaktor wird – wenn nicht explizit etwas Anderes vermerkt ist – stets zu $H(f$ = 0) = 1 angenommen.
Aus jeder Tiefpassfunktion lassen sich entsprechende Hochpassfunktionen ableiten, wie auf der letzten Theorieseite dieses Abschnitts gezeigt wird.

Idealer Tiefpass – Küpfmüller–Tiefpass (1)

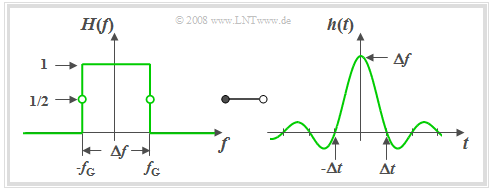
Definition: Man bezeichnet einen Tiefpass als ideal, wenn sein Frequenzgang wie folgt lautet: $$H(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ 0.5 \\\hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad\begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\{\left| \hspace{0.005cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\{\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\\end{array}$$ Wir verwenden teilweise auch die Bezeichnung „Küpfmüller-Tiefpass” (KTP) in Erinnerung an den Pionier der Systemtheorie, Karl Küpfmüller.

Die Grafik zeigt einen solchen idealen Tiefpass im Frequenz– und Zeitbereich.

Man erkennt aus diesem Kurvenverläufen:

Aufgrund des abrupten, unendlich steilen Flankenabfalls ist hier die 3dB–Grenzfrequenz $f_G$ genau halb so groß wie die systemtheoretische Bandbreite $Δf$.
Alle Spektralanteile mit $f$ < $f_G$ werden unverfälscht durchgelassen (Durchlassbereich), alle Anteile mit $f$ > $f_G$ vollständig unterdrückt (Sperrbereich). Bei $f$ = $f_G$ gilt $H(f)$ = 0.5.

Hinweis: Die Beschreibung im Zeitbereich finden Sie nachfolgend.

Idealer Tiefpass – Küpfmüller–Tiefpass (2)

Kommen wir nun zur Beschreibung des idealen Tiefpasses im Zeitbereich:

Die Impulsantwort ergibt sich entsprechend der Fourierrücktransformation zu

$$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t)\hspace{0.7cm}{\rm{mit}}\hspace{0.7cm}{\rm si}(x) =\frac{\sin(x)}{x}.$$

Die beidseitig bis ins Unendliche ausgedehnte Zeitfunktion weist äquidistante Nulldurchgänge im Abstand $Δt$ = 1/ $Δf$ auf (siehe rechte untere

Grafik).

Der asymptotische Abfall erfolgt umgekehrt proportional mit der Zeit:

$$|h(t)| = \frac{\Delta f}{\pi \cdot \Delta f \cdot |t|} \cdot \left |{\rm sin}(\pi \cdot \Delta f\cdot t )\right | \le \frac{1}{\pi \cdot |t|}.$$

Daraus folgt, dass die Impulsantwort erst für Zeiten $t$ > $t_{1‰}$ = 318 · $Δt$ mit Sicherheit kleiner als 1‰ des Impulsmaximums ist.
Die Sprungantwort ergibt sich aus der Impulsantwort durch Integration und lautet:

$${\rm \sigma}(t) = \int\limits_{ - \infty }^{ t } {h ( \tau )} \hspace{0.1cm}{\rm d}\tau = \frac{1}{2} + \frac{1}{\pi} \cdot {\rm Si}(\pi \cdot\Delta f \cdot t ).$$

Hierbei ist die so genannte Integral–Sinusfunktion

$${\rm Si}(x) = \int\limits_{ 0 }^{ x } {{\rm si} ( \xi )} \hspace{0.1cm}{\rm d}\xi = x - \frac{x^3}{3 \cdot 3!} + \frac{x^5}{5 \cdot 5!} - \frac{x^7}{7 \cdot 7!}+ ...$$

verwendet, die folgende Eigenschaften besitzt:

$${\rm Si}(0) = 0, \hspace{0.3cm}{\rm Si}(\infty) = \frac{\pi}{2}, \hspace{0.3cm}{\rm Si}(-x) = -{\rm Si}(x).$$

Hinweis: In manchen Büchern wird statt der Funktion $si(x)$ die ähnliche Funktion $sinc(x)$ verwendet: $${\rm si}(x) = \frac{\sin(x)}{x}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{\rm sinc}(x) = \frac{\sin(\pi x)}{\pi x} = {\rm si}(\pi x).$$ In diesem Fall lautet die Impulsantwort des idealen Tiefpasses $h(t)$ = $Δf · sinc(Δf · t).$