Laplace–Rücktransformation

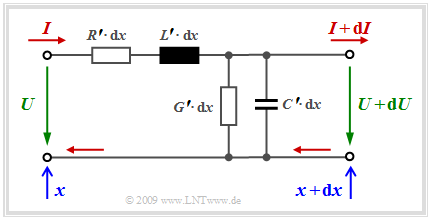
Ersatzschaltbild eines kurzen Leitungsabschnitts (1)

Zur Herleitung der Leitungsgleichungen wird zunächst ein sehr kurzer Leitungsabschnitt der Länge $dx$ betrachtet, so dass sich die Werte für Spannung und Strom am Leitungsanfang $(U$ bzw. $I$ bei $x)$ und am Leitungsende $(U + dU$ sowie $I + dI$ bei $x + dx)$ nur geringfügig unterscheiden. Die Grafik zeigt das zugrundeliegende Modell.

Anders ausgedrückt: Die Leitungslänge $dx$ sei sehr klein gegenüber der Wellenlänge der sich entlang der Leitung ausbreitenden elektromagnetischen Welle, die sich ergibt, da

mit dem Strom ein magnetisches Feld verbunden ist,
die Spannung zwischen den Leitern ein elektrisches Feld bewirkt.

Alle infinitesimalen „Bauelemente” im oben skizzierten Ersatzschaltbild sind bei homogenen Leitungen ortsunabhängig:

Die Induktivität des betrachteten Leitungsabschnitts beträgt $L' · dx$, wobei man die auf die Länge $dx$ bezogene Größe als Induktivitätsbelag bezeichnet.
Ebenso ist der Kapazitätsbelag $C'$ eine infinitesimal kleine Größe, der ebenso wie $L'$ nur relativ wenig von der Frequenz abhängt.
Der Ableitungsbelag $G'$ berücksichtigt die Verluste des Dielektrikums zwischen den Drähten. Er nimmt etwa proportional mit der Frequenz zu.
Den weitaus größten Einfluss auf die Signalübertragung hat der Widerstandsbelag $R'$, der für hohe Frequenzen aufgrund des dann dominanten Skineffekts nahezu proportional mit der Wurzel der Frequenz ansteigt.