Gleichverteilte Zufallsgrößen

Allgemeine Beschreibung und Definition

Eine Zufallsgröße $x$ bezeichnet man als gleichverteilt, wenn sie nur Werte im Bereich von $x_{\rm min}$ bis $x_{\rm max}$ annehmen kann, und zwar mit gleicher Wahrscheinlichkeit.

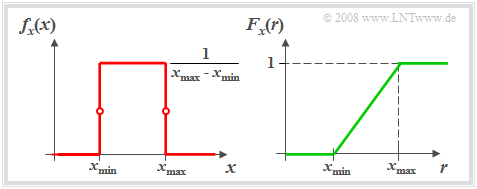
Die Grafik zeigt links die Wahrscheinlichkeitsdichtefunktion (abgekürzt WDF) und rechts die Verteilungsfunktion (kurz VTF) einer gleichverteilten Zufallsgröße $x$.

Daraus können folgende Eigenschaften abgeleitet werden:

Die WDF $f_{\rm x}(x)$ besitzt im Bereich von $x_{\rm min}$ bis $x_{\rm max}$ den konstanten Wert $1/(x_{\rm max} - x_{\rm min})$, wobei an den beiden Bereichsgrenzen für $f_{\rm x}(x)$ jeweils nur der halbe Wert – also der Mittelwert zwischen links- und rechtsseitigem Grenzwert – zu setzen ist.
Die Verteilungsfunktion $F_{\rm x}(r)$ steigt im Bereich von $x_{\rm min}$ bis $x_{\rm max}$ linear von 0 auf 1 an.
Mittelwert und Streuung haben bei der Gleichverteilung die folgenden Werte:

$$m_{\rm 1} = \frac{\it x_ {\rm max} + \it x_{\rm min}}{2},\hspace{0.5cm} \sigma = \frac{\it x_{\rm max} - \it x_{\rm min}}{2 \sqrt{3}}.$$

Bei symmetrischer WDF $(x_{\rm min} = –x_{\rm max})$ erhält man als Sonderfall $m_1 =$ 0 und $σ^2 = x_{\rm max}^2/3.$

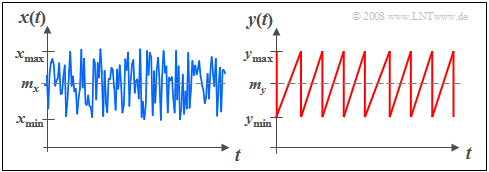
Hier sehen Sie zwei Signalverläufe mit gleichförmiger Amplitudenverteilung.

Links ist statistische Unabhängigkeit der einzelnen Abtastwerte vorausgesetzt, das heißt, $x_ν$ kann alle Werte zwischen $x_{\rm min}$ und $x_{\rm max}$ mit gleicher Wahrscheinlichkeit annehmen, und zwar unabhängig von der Vergangenheit $(x_{ν–1}, x_{ν–2}, ...).$
Beim rechten Signal $y(t)$ ist diese Unabhängigkeit aufeinanderfolgender Signalwerte nicht mehr gegeben. Vielmehr stellt dieses Sägezahnsignal ein deterministisches Signal dar.

Bedeutung der Gleichverteilung für die Nachrichtentechnik

Die Bedeutung gleichverteilter Zufallsgrößen für die Informations- und Kommunikationstechnik ist darauf zurückzuführen, dass diese WDF–Form aus Sicht der Informationstheorie unter der Nebenbedingung „Spitzenwertbegrenzung” ein Optimum darstellt. Mit keiner anderen Verteilung als der Gleichverteilung erreicht man unter dieser Voraussetzung eine größere differentielle Entropie. Mit dieser Thematik beschäftigt sich das Kapitel 4.1 im Buch „Einführung in die Informationstheorie”.

Daneben sind unter Anderem noch folgende Punkte zu nennen:

Die Bedeutung der Gleichverteiltung für die Simulation nachrichtentechnischer Systeme ist darauf zurückzuführen, dass man entsprechende Pseudo–Zufallsgeneratoren relativ einfach realisieren kann, und dass sich daraus andere Verteilungen (zum Beispiel die Gauß–, die Laplace– und die Exponentialverteilung) leicht ableiten lassen (vgl. Kapitel 3.5 bis 3.7).
In Bildverarbeitung & Bildcodierung wird häufig vereinfachend mit der Gleichverteilung anstelle der tatsächlichen, meist sehr viel komplizierteren Verteilung des Originalbildes gerechnet, da der Unterschied des Informationsgehaltes zwischen einem natürlichen Bild und dem auf der Gleichverteilung basierenden Modell relativ gering ist.
Für die Modellierung übertragungstechnischer Systeme sind gleichverteilte Zufallsgrößen dagegen die Ausnahme. Ein Beispiel für eine tatsächlich (nahezu) gleichverteilte Zufallsgröße ist die Phase bei kreissymmetrischen Störungen, wie sie beispielsweise bei Quadraturmodulationsverfahren auftreten.

Das folgende Tool berechnet unter Anderem die Kenngrößen der Gleichverteilung für beliebige Parameter $x_{\rm min}$ und $x_{\rm max}$: WDF, VTF und Momente spezieller Verteilungen

Hinweis: In dieser Multimedia–Anwendung wird die Gleichverteilung als „Rechteck” bezeichnet.