Zweidimensionale Zufallsgrößen
Eigenschaften und Beispiele
Als Überleitung zu den Korrelationsfunktionen betrachten wir nun zwei Zufallsgrößen $x$ und $y$, zwischen denen statistische Abhängigkeiten bestehen. Jede der beiden Zufallsgrößen kann für sich alleine mit den in Kapitel 2 bzw. Kapitel 3 eingeführten Kenngrößen beschrieben werden, je nachdem, ob es sich um eine diskrete oder um eine kontinuierliche Zufallsgröße handelt.
Zur Beschreibung der Wechselbeziehungen zwischen zwei Größen $x$ und $y$ ist es zweckmäßig, die beiden Komponenten zu einer zweidimensionalen Zufallsgröße $(x, y)$ zusammenzufassen. Die Einzelkomponenten können Signale sein wie der Real- und Imaginärteil eines phasenmodulierten Signals. Aber es gibt auch in anderen Bereichen eine Vielzahl von 2D-Zufallsgrößen.
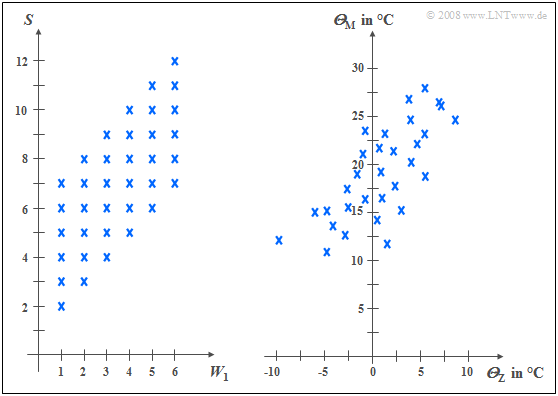
Das folgende linke Diagramm stammt von dem Zufallsexperiment Werfen mit zwei Würfeln. Nach rechts aufgetragen ist die Augenzahl des ersten Würfels $(W_1)$, nach oben die Summe $S$ beider Würfel. Die beiden Komponenten sind hier jeweils diskrete Zufallsgrößen, zwischen denen statistische Bindungen bestehen. Ist $W_1 =$ 1, so kann $S$ nur Werte zwischen 2 und 7 annehmen und zwar mit jeweils gleicher Warscheinlichkeit, bei $W_1 =$ 6 dagegen die Werte zwischen 7 und 12.
Rechts sind die Maximaltemperaturen der 31 Tage im Mai 2002 von München (nach oben) und der Zugspitze (nach rechts) gegenübergestellt. Beide Zufallsgrößen sind wertkontinuierlich. Obwohl die Messpunkte etwa 100 km auseinander liegen und es auf der Zugspitze aufgrund der unterschiedlichen Höhenlagen (knapp 3000 gegenüber 520 Meter) im Mittel um etwa 20 Grad kälter ist als in München, erkennt man doch eine gewisse statistische Abhängigkeit zwischen den beiden Größen $Θ_{\rm M}$ und $Θ_{\rm Z}$: Ist es in München warm, dann sind auch auf der Zugspitze eher angenehme Temperaturen zu erwarten. Der Zusammenhang ist aber nicht deterministisch: Der kälteste Tag im Mai 2002 war in München ein anderer als der kälteste Tag auf der Zugspitze.