Kreuzkorrelationsfunktion und Kreuzleistungsdichte
Definition der Kreuzkorrelationsfunktion
Bei vielen technischen Anwendungen interessiert man sich für ein quantitatives Maß zur Beschreibung der statistischen Verwandtschaft zwischen verschiedenen Prozessen bzw. zwischen deren Mustersignalen. Ein solches Maß ist die Kreuzkorrelationsfunktion (KKF), die hier unter den Voraussetzungen von Stationarität und Ergodizität hergeleitet wird.
Für die Kreuzkorrelationsfunktion zweier stationärer und ergodischer Prozesse mit den Musterfunktionen $x(t)$ und $y(t)$ gilt: $$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\rm d \it t.$$
Die erste Definitionsgleichung kennzeichnet die Erwartungswertbildung (Scharmittelung), während die zweite Gleichung die Zeitmittelung über eine (möglichst große) Messdauer $T_{\rm M}$ beschreibt.
Ein Vergleich mit der AKF-Definition zeigt viele Gemeinsamkeiten mit dieser. Setzt man $y(t) = x(t)$, so erhält man $φ_{xy}(τ) = φ_{xx}(τ)$, also die Autokorrelationsfunktion, für die in Abschnitt 4.4 die vereinfachte Schreibweise $φ_x(τ)$ eingeführt wurde.
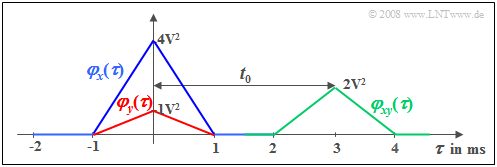
Wir betrachten ein Zufallssignal $x(t)$ mit dreieckförmiger AKF $φ_x(τ)$ ⇒ blaue Kurve. Diese AKF–Form ergibt sich zum Beispiel für ein Binärsignal mit gleichwahrscheinlichen bipolaren Amplitudenkoeffizienten (+1 bzw. –1) und bei rechteckförmigem Grundimpuls.
Betrachten wir dazu noch ein zweites Signal
$$y(t) = \alpha \cdot x (t - t_{\rm 0}),$$
das sich von $x(t)$ nur durch einen Dämpfungsfaktor $α$ und eine Laufzeit $t_0$ unterscheidet, wobei dem obigen Bild $α =$ 0.5 und $t_0 =$ 3 ms zugrunde liegen. Dieses gedämpfte und verschobene Signal besitzt die rot gezeichnete AKF
$$\varphi_{y}(\tau) = \alpha^2 \cdot \varphi_{x}(\tau) .$$
Die Verschiebung um $t_0$ ist in der AKF nicht zu erkennen im Gegensatz zur (grün dargestellten) KKF, für die folgende Beziehung gilt:
$$\varphi_{xy}(\tau) = \alpha \cdot \varphi_{x}(\tau- t_{\rm 0}) .$$
Eigenschaften der Kreuzkorrelationsfunktion
Nachfolgend sind wesentliche Eigenschaften der Kreuzkorrelationsfunktion zusammengestellt und die wichtigsten Unterschiede zur AKF herausgearbeitet.
- Die Bildung der Kreuzkorrelationsfunktion ist nicht kommutativ. Vielmehr gibt es stets zwei unterschiedliche Funktionen, nämlich
$$\varphi_{xy}(\tau)={\rm E} [{x(t)\cdot y(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}x(t)\cdot y(t+\tau)\,\, \rm d \it t,$$ $$\varphi_{yx}(\tau)={\rm E} [{y(t)\cdot x(t+\tau)}]=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}/{\rm 2}}_{-T_{\rm M}/{\rm 2}}y(t)\cdot x(t+\tau)\,\, \rm d \it t .$$
- Zwischen den beiden Funktionen besteht der Zusammenhang $φ_{yx}(τ) = φ_{xy}(–τ)$. Im Beispiel des letzten Abschnitts hätte $φ_{yx}(τ)$ sein Maximum bei $τ =$ –3 ms.
- Im Allgemeinen tritt das KKF-Maximum nicht bei $τ =$ 0 auf (Ausnahme: $y = α · x$) und dem KKF-Wert $φ_{xy}(τ = 0)$ kommt keine besondere, physikalisch interpretierbare Bedeutung zu wie bei der AKF, bei der dieser Wert die Prozessleistung wiedergibt.
- Der Betrag der KKF ist nach der Schwarzschen Ungleichung für alle $τ$-Werte kleiner oder gleich dem geometrischen Mittel der beiden Signalleistungen: