Matched-Filter

Optimierungskriterium des Matched–Filters

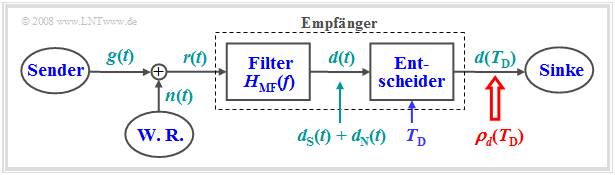
Das Matched-Filter – auch Korrelationsfilter genannt – dient zum Nachweis der Signalexistenz. Es kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem SNR – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht. Zur Herleitung des Matched-Filters wird folgende Anordnung betrachtet.

Blockschaltbild des Matched-Filter-Empfängers

Für die einzelnen Komponenten gelten folgende Voraussetzungen:

Der Nutzanteil $g(t)$ des Empfangssignals $r(t)$ sei impulsförmig und somit energiebegrenzt. Das heißt: Das Integral über $g^2(t)$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$.
Das Störsignal $n(t)$ sei Weißes Gaußsches Rauschen mit der Rauschleistungsdichte $N_0$.
Das Filterausgangssignal $d(t)$ setzt sich additiv aus zwei Anteilen zusammen. Der Anteil $d_{\rm S}(t)$ geht auf das „Signal” $g(t)$ zurück und der Anteil $d_{\rm N}(t)$ auf das „Noise” $n(t)$.
Der Empfänger, bestehend aus linearem Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird:

$$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma _d ^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$

Hierbei bezeichnen $σ_d^2$ die Varianz (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den Detektionszeitpunkt.