Matched-Filter

1. Stochastische Signaltheorie
2. Filterung stochastischer Signale
3. Matched-Filter

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Optimierungskriterium des Matched–Filters

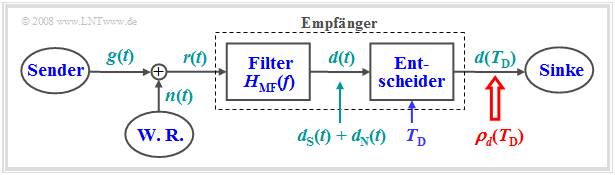
Das Matched-Filter – auch Korrelationsfilter genannt – dient zum Nachweis der Signalexistenz. Es kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem SNR – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht. Zur Herleitung des Matched-Filters wird folgende Anordnung betrachtet.

Für die einzelnen Komponenten gelten folgende Voraussetzungen:

• Der Nutzanteil $g(t)$ des Empfangssignals $r(t)$ sei impulsförmig und somit energiebegrenzt. Das heißt: Das Integral über $g^2(t)$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$.
• Das Störsignal $n(t)$ sei Weißes Gaußsches Rauschen mit der Rauschleistungsdichte $N_0$.
• Das Filterausgangssignal $d(t)$ setzt sich additiv aus zwei Anteilen zusammen. Der Anteil $d_{\rm S}(t)$ geht auf das „Signal” $g(t)$ zurück und der Anteil $d_{\rm N}(t)$ auf das „Noise” $n(t)$.
• Der Empfänger, bestehend aus linearem Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird:

$$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma _d ^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$

Hierbei bezeichnen $σ_d^2$ die Varianz (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den Detektionszeitpunkt.

Matched-Filter-Optimierung (1)

Gegeben sei ein energiebegrenztes Nutzsignal $g(t)$ mit dem zugehörigen Spektrum $G(f)$. Damit kann das Filterausgangssignal zum Detektionszeitpunkt $T_{\rm D}$ für jedes beliebige Filter mit der Impulsantwort $h(t)$ und dem Frequenzgang $H(f) = F${ $h(t)$} wie folgt geschrieben werden (ohne Berücksichtigung des Rauschens ⇒ Index S für „Signal”): $$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{{\rm{j}}2{\rm{\pi }}fT_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$ Der „Rauschanteil” $d_{\rm N}(t)$ des Filterausgangssignals rührt allein vom Weißen Rauschen $n(t)$ am Eingang des Empfängers her. Für seine Varianz (Leistung) gilt unabhängig von $T_{\rm D}$: $$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$ Damit lautet das hier vorliegende Optimierungsproblem: $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{{\rm{j} }2{\rm{\pi } }fT_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$ Man kann zeigen, dass der Quotient für den folgenden Frequenzgang am größten wird: $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e}}^{-{\rm{j}}2{\rm{\pi }}fT_{\rm D} } .$$ Damit erhält man für das Signal-zu-Rauschleistungsverhältnis am Matched–Filter–Ausgang: $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } },$$ und zwar unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF}$. Zur Erklärung:

• $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:

$$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d}}t} = \int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2}}\hspace{0.1cm} {\rm d}f} .$$

Ein rechteckförmiger Impuls $g(t)$ mit der Amplitude $\rm 1V$ und der Dauer 0.5ms und unbekannter Lage soll in einer verrauschten Umgebung aufgefunden werden. Somit ist die Impulsenergie $E_g = \rm 5 · 10^{–4} V^2s$. Die Rauschleistungsdichte sei $N_0 = \rm 10^{–6} V^2/Hz$.

Das beste Ergebnis ⇒ maximale S/N–Verhältnis erzielt man mit dem Matched-Filter: $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$

Die Matched-Filter-Optimierung wird im nächsten Abschnitt hergeleitet. Wenn Sie daran nicht interessiert sind, fahren Sie bitte mit der Seite Interpretation des Matched-Filters fort.

Matched-Filter-Optimierung (2)

Das im letzten Abschnitt angegebene Matched–Filter–Kriterium wird nun schrittweise hergeleitet. Wenn Sie daran nicht interessiert sind, so springen Sie bitte zur Fortsetzungsseite Interpretation des Matched–Filters.

Herleitung des Matched–Filter–Kriteriums: Die Schwarzsche Ungleichung lautet mit den beiden (im allgemeinen komplexen) Funktionen $A(f)$ und $B(f)$: $$\left| {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right|^2 \le \int_a^b {\left| {A(f)} \right|^{\rm{2} } \hspace{0.1cm}{\rm{d}}f} \cdot \int_a^b {\left| {B(f)} \right|^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$ Wir wenden nun diese Gleichung auf das Signal–zu–Rauschverhältnis an: $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm{j} }2{\rm{\pi } }fT_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$ Mit $A(f) = G(f)$ und $B(f) = H(f) · {\rm exp}({\rm j2}πfT_{\rm D})$ ergibt sich somit die folgende Schranke: $$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$ Setzt man für den Filterfrequenzgang versuchsweise $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{ {\rm{ - j} }2{\rm{\pi } }fT_{\rm D} }$$ ein, so erhält man aus der obigen Gleichung: $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$

Das heißt: Mit diesem Ansatz für das Matched-Filter $H_{\rm MF}(f)$ wird in obiger Abschätzung tatsächlich der maximal mögliche Wert erreicht. Mit keinem anderen Filter $H(f) ≠ H_{\rm MF}(f)$ kann man ein höheres Signal–zu–Rauschleistungsverhältnis erzielen ⇒ Das Matched–Filter ist in Bezug auf das ihm zugrunde gelegte Maximierungskriterium optimal.

q.e.d.

Interpretation des Matched-Filters

Auf der letzten Seite wurde der Frequenzgang des Matched-Filters wie folgt abgeleitet: $$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{ {\rm{ - j} }2{\rm{\pi } }fT_{\rm D} } .$$ Durch Fourierrücktransformation erhält man die dazugehörige Impulsantwort: $$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$

Diese beiden Funktionen lassen sich wie folgt interpretieren:

• Das Matched-Filter ist durch den Term $G^{\star}(f)$ an das Spektrum des aufzufindenden Impulses $g(t)$ angepasst – daher sein Name (englisch: to match ≡ anpassen).
• Die Konstante $K_{\rm MF}$ ist aus Dimensionsgründen notwendig. Ist $g(t)$ ein Spannungsimpuls, so hat diese Konstante die Einheit „Hz/V”. Der Frequenzgang ist somit dimensionslos.
• Die Impulsantwort $h_{\rm MF}(t)$ ergibt sich aus dem Nutzsignal $g(t)$ durch Spiegelung ⇒ aus $g(t)$ wird $g(–t)$ – sowie einer Verschiebung um $T_{\rm D}$ nach rechts.
• Der früheste Detektionszeitpunkt $T_{\rm D}$ folgt für realisierbare Systeme aus der Bedingung $h_{\rm MF}(t < 0)$ ≡ 0 ⇒ „Kausalität” (siehe Buch Lineare zeitinvariante Systeme ).
• Für den Nutzanteil des Filterausgangssignals gilt: