Matched-Filter

1. Stochastische Signaltheorie
2. Filterung stochastischer Signale
3. Matched-Filter

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Optimierungskriterium des Matched–Filters

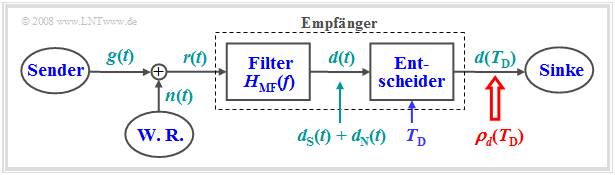
Das Matched-Filter – auch Korrelationsfilter genannt – dient zum Nachweis der Signalexistenz. Es kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem SNR – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht. Zur Herleitung des Matched-Filters wird folgende Anordnung betrachtet.

Für die einzelnen Komponenten gelten folgende Voraussetzungen:

• Der Nutzanteil $g(t)$ des Empfangssignals $r(t)$ sei impulsförmig und somit energiebegrenzt. Das heißt: Das Integral über $g^2(t)$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$.
• Das Störsignal $n(t)$ sei Weißes Gaußsches Rauschen mit der Rauschleistungsdichte $N_0$.
• Das Filterausgangssignal $d(t)$ setzt sich additiv aus zwei Anteilen zusammen. Der Anteil $d_{\rm S}(t)$ geht auf das „Signal” $g(t)$ zurück und der Anteil $d_{\rm N}(t)$ auf das „Noise” $n(t)$.
• Der Empfänger, bestehend aus linearem Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird:

$$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma _d ^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$

Hierbei bezeichnen $σ_d^2$ die Varianz (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den Detektionszeitpunkt.

Matched-Filter-Optimierung (1)

Gegeben sei ein energiebegrenztes Nutzsignal $g(t)$ mit dem zugehörigen Spektrum $G(f)$. Damit kann das Filterausgangssignal zum Detektionszeitpunkt $T_{\rm D}$ für jedes beliebige Filter mit der Impulsantwort $h(t)$ und dem Frequenzgang $H(f) = F${ $h(t)$} wie folgt geschrieben werden (ohne Berücksichtigung des Rauschens ⇒ Index S für „Signal”): $$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{{\rm{j}}2{\rm{\pi }}fT_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$ Der „Rauschanteil” $d_{\rm N}(t)$ des Filterausgangssignals rührt allein vom Weißen Rauschen $n(t)$ am Eingang des Empfängers her. Für seine Varianz (Leistung) gilt unabhängig von $T_{\rm D}$: $$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$ Damit lautet das hier vorliegende Optimierungsproblem: $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{{\rm{j} }2{\rm{\pi } }fT_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$ Man kann zeigen, dass der Quotient für den folgenden Frequenzgang am größten wird: $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e}}^{-{\rm{j}}2{\rm{\pi }}fT_{\rm D} } .$$ Damit erhält man für das Signal-zu-Rauschleistungsverhältnis am Matched–Filter–Ausgang: $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } },$$ und zwar unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF}$. Zur Erklärung:

• $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:

$$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d}}t} = \int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2}}\hspace{0.1cm} {\rm d}f} .$$

Ein rechteckförmiger Impuls $g(t)$ mit der Amplitude $\rm 1V$ und der Dauer 0.5ms und unbekannter Lage soll in einer verrauschten Umgebung aufgefunden werden. Somit ist die Impulsenergie $E_g = \rm 5 · 10^{–4} V^2s$. Die Rauschleistungsdichte sei $N_0 = \rm 10^{–6} V^2/Hz$.

Das beste Ergebnis ⇒ maximale S/N–Verhältnis erzielt man mit dem Matched-Filter: $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$

Die Matched-Filter-Optimierung wird im nächsten Abschnitt hergeleitet. Wenn Sie daran nicht interessiert sind, fahren Sie bitte mit der Seite Interpretation des Matched-Filters fort.

Matched-Filter-Optimierung (2)

Das im letzten Abschnitt angegebene Matched–Filter–Kriterium wird nun schrittweise hergeleitet. Wenn Sie daran nicht interessiert sind, so springen Sie bitte zur Fortsetzungsseite Interpretation des Matched–Filters.

Herleitung des Matched–Filter–Kriteriums: Die Schwarzsche Ungleichung lautet mit den beiden (im allgemeinen komplexen) Funktionen $A(f)$ und $B(f)$: $$\left| {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right|^2 \le \int_a^b {\left| {A(f)} \right|^{\rm{2} } \hspace{0.1cm}{\rm{d}}f} \cdot \int_a^b {\left| {B(f)} \right|^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$ Wir wenden nun diese Gleichung auf das Signal–zu–Rauschverhältnis an: $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{ {\rm{j} }2{\rm{\pi } }fT_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$ Mit $A(f) = G(f)$ und $B(f) = H(f) · {\rm exp}({\rm j2}πfT_{\rm D})$ ergibt sich somit die folgende Schranke: $$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$ Setzt man für den Filterfrequenzgang versuchsweise $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{ {\rm{ - j} }2{\rm{\pi } }fT_{\rm D} }$$ ein, so erhält man aus der obigen Gleichung: $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left| {G(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$

Das heißt: Mit diesem Ansatz für das Matched-Filter $H_{\rm MF}(f)$ wird in obiger Abschätzung tatsächlich der maximal mögliche Wert erreicht. Mit keinem anderen Filter $H(f) ≠ H_{\rm MF}(f)$ kann man ein höheres Signal–zu–Rauschleistungsverhältnis erzielen ⇒ Das Matched–Filter ist in Bezug auf das ihm zugrunde gelegte Maximierungskriterium optimal.

q.e.d.

Interpretation des Matched-Filters

Auf der letzten Seite wurde der Frequenzgang des Matched-Filters wie folgt abgeleitet: $$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{ {\rm{ - j} }2{\rm{\pi } }fT_{\rm D} } .$$ Durch Fourierrücktransformation erhält man die dazugehörige Impulsantwort: $$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$

Diese beiden Funktionen lassen sich wie folgt interpretieren:

• Das Matched-Filter ist durch den Term $G^{\star}(f)$ an das Spektrum des aufzufindenden Impulses $g(t)$ angepasst – daher sein Name (englisch: to match ≡ anpassen).
• Die Konstante $K_{\rm MF}$ ist aus Dimensionsgründen notwendig. Ist $g(t)$ ein Spannungsimpuls, so hat diese Konstante die Einheit „Hz/V”. Der Frequenzgang ist somit dimensionslos.
• Die Impulsantwort $h_{\rm MF}(t)$ ergibt sich aus dem Nutzsignal $g(t)$ durch Spiegelung ⇒ aus $g(t)$ wird $g(–t)$ – sowie einer Verschiebung um $T_{\rm D}$ nach rechts.
• Der früheste Detektionszeitpunkt $T_{\rm D}$ folgt für realisierbare Systeme aus der Bedingung $h_{\rm MF}(t < 0)$ ≡ 0 ⇒ „Kausalität” (siehe Buch Lineare zeitinvariante Systeme ).
• Für den Nutzanteil des Filterausgangssignals gilt:

$$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$

Das bedeutet: Das Ausgangssignal ist formgleich mit der Energie-AKF (in diesem Tutorial durch einen Punkt gekennzeichnet) und gegenüber dieser um $T_{\rm D}$ verschoben.

Anmerkung: Bei einem energiebegrenzten Signal $g(t)$ kann man nur die Energie–AKF angeben: $$\varphi^{^{\bullet}}_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d}}t} .$$ Gegenüber der AKF-Definition eines leistungsbegrenzten Signals $x(t)$, nämlich $$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_M } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$ wird bei der Berechnung der Energie-AKF auf die Division durch die Messdauer $T_{\rm M}$ sowie auf den Grenzübergang $T_{\rm M} → ∞$ verzichtet.

Wir gehen davon aus, dass gemäß dem letzten Beispiel der Rechteckimpuls zwischen 2ms und 2.5ms liegt und der Detektionszeitpunkt $T_{\rm D} =$ 4 ms gewünscht wird. Dann gilt:

• Die Matched–Filter–Impulsantwort $h_{\rm MF}(t)$ muss im Bereich von $t_1 (= 4 – 2.5) =$ 1.5ms bis $t_2 (= 4 – 2) =$ 2ms konstant sein. Für $t < t_1$ sowie für $t > t_2$ darf sie keine Anteile besitzen.
• Der Betragsfrequenzgang $|H_{\rm MF}(f)|$ ist hier si–förmig. Die Höhe der Impulsantwort $h_{\rm MF}(t)$ spielt für das S/N–Verhältnis keine Rolle, da dieses unabhängig von $K_{\rm MF}$ ist.

Matched-Filter bei farbigen Störungen (1)

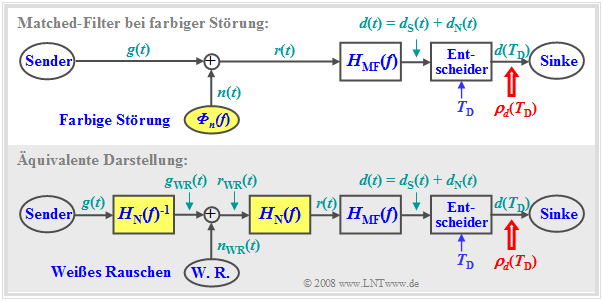
Bei den Herleitungen dieses Abschnittes wurde bisher stets von Weißem Rauschen ausgegangen. Nun soll die Frage geklärt werden, wie das Empfangsfilter $H(f) = H_{\rm MF}(f)$ bei farbiger Störung $n(t)$ zu gestalten ist, damit das Signal–zu–Rauschleistungsverhältnis maximal wird.

Hinweis: Der Begriff „Störung” ist etwas allgemeiner als „Rauschen”. Vielmehr ist Rauschen eine Teilmenge aller Störungen, zu denen z. B. auch das Nebensprechen von benachbarten Leitungen zählt. Wir sprechen nur dann von (weißem) Rauschen $n(t)$, wenn das Leistungsdichtespektrum ${\it Φ}_n(f)$ für alle Frequenzen gleich ist. Ist dies nicht erfüllt, so bezeichnen wir $n(t)$ als farbige Störung.

Zu dem hier betrachteten Modell ist zu bemerken:

• Die obere Grafik zeigt das Blockschaltbild zur Herleitung des Matched–Filters $H_{\rm MF}(f)$ bei farbiger Störung $n(t)$, gekennzeichnet durch das Leistungsdichtespektrum ${\it Φ}_n(f) ≠$ const. Alle bisher für diesen Abschnitt genannten Voraussetzungen gelten weiterhin.
• Das farbige Störsignal $n(t)$ mit dem Leistungsdichtespektrum ${\it Φ}_n(f)$ kann man – zumindest gedanklich – durch eine „weiße” Rauschquelle $n_{\rm WR}(t)$ mit der konstanten (zweiseitigen) Rauschleistungsdichte $N_0/2$ und ein Formfilter mit dem Frequenzgang $H_{\rm N}(f)$ modellieren:

$${\it{\Phi} }_n \left( f \right) = { {N_{\rm 0} } }/{\rm 2} \cdot \left| {H_{\rm N} \left( f \right)} \right|^{\rm 2} .$$

• Diese Modifikation ist in der unteren Grafik berücksichtigt. Da Realisierungsaspekte hier nicht betrachtet werden, wird $H_{\rm N}(f)$ vereinfacht als reell angenommen. Der Phasengang von $H_{\rm N}(f)$ spielt für das Folgende keine Rolle.
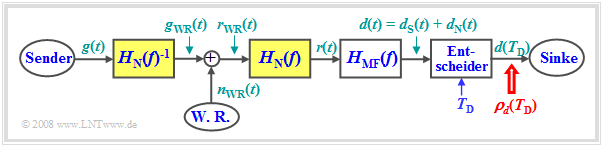
• In der unteren Darstellung ist das Formfilter $H_{\rm N}(f)$ auf die rechte Seite der Störaddition verschoben. Um ein auch bezüglich des Nutzsignals $d_{\rm S}(t)$ äquivalentes Modell zu erhalten, wird das Formfilter im Nutzsignalzweig durch das inverse Filter $H_{\rm N}(f)^{–1}$ kompensiert.

Matched-Filter bei farbigen Störungen (2)

Anhand dieses modifizierten Modells wird nun das verallgemeinerte Matched-Filter für den Fall farbiger Störungen hergeleitet. Besitzt $H_{\rm N}(f)$ keine Nullstelle, was für das Folgende vorausgesetzt werden soll, so ist diese Anordnungen mit dem Blockschaltbild (obere Grafik im letzten Abschnitt) identisch.

An der Störadditionsstelle liegt nun weißes Rauschen $n_{\rm WR}(t)$ an. Die Herleitung der Matched–Filter–Optimierung bei weißem Rauschen lässt sich 1 zu 1 auf das aktuelle Problem anpassen, wenn man Folgendes berücksichtigt:

• Anstelle des tatsächlichen Sendesignals $g(t)$ ist das Signal $g_{\rm WR}(t)$ vor der Störaddition zu berücksichtigen. Die dazugehörige Spektralfunktion lautet: $G_{\rm WR}(f) = G(f)/H_{\rm N}(f)$.
• Anstelle von $H_{\rm MF}(f)$ ist nun der resultierende Frequenzgang $H_{\rm MF}'(f) = H_{\rm N}(f) · H_{\rm MF}$ rechts von der Störadditionsstelle einzusetzen.

Damit ergibt sich für das Matched-Filter bei farbigen Störungen: $${H_{\rm MF} }' (f) = H_{\rm N} (f) \cdot H_{\rm MF} (f) = K_{\rm MF} \cdot G_{\rm WR} ^ {\star} (f) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }fT_{\rm D} } $$ $$\Rightarrow \hspace{0.3cm}H_{\rm MF} (f) = K_{\rm MF} \cdot \frac{ {G^{\star} (f)} }{ {\left| {H_{\rm N} (f)} \right|^2 } } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }fT_{\rm D} } .$$ Das Signal-zu-Störleistungsverhältnis vor dem Entscheider ist somit maximal: $$\rho _{d,\max } ( {T_{\rm D} } ) = \frac{1}{ {N_0 /2} }\int_{ - \infty }^{ + \infty } {\left| {G_{\rm WR} (f)} \right|^2 }\, {\rm{d} }f = \int\limits_{ - \infty }^{ + \infty } \frac{\left| G(f) \right|^2 }{ {\it{\Phi _n (f)} } } \,{\rm{d} }f.$$

Der Fall „Weißes Rauschen” ist in dieser allgemeineren Gleichung für ${\it Φ}_n(f) = N_0/2$ mitenthalten.

Hinweis: Alle auf dieser Seite angegebenen Gleichungen führen bei farbiger Störung allerdings nur dann zu sinnvollen, auch in der Praxis verwertbaren Ergebnissen, wenn das Energiespektrum $|G(f)|^2$ des Nutzsignals asymptotisch schneller abklingt als das Störleistungsdichtespektrum ${\it Φ}_n(f)$.