Zielsetzung von Modulation und Demodulation
Inhaltsverzeichnis
Betrachtetes Nachrichtenübertragungssystem
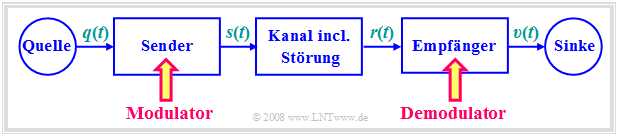
Im gesamten Buch wird von folgendem Blockschaltbild ausgegangen:
Hierzu ist anzumerken:
- Das zur Übertragung anstehende Quellensignal $q(t)$ sei ein Analogsignal, zum Beispiel Sprache, Musik oder der Ausgang einer (analogen) Videokamera. Das zugehörige Spektrum $Q(f)$ sei auf den Frequenzbereich $|f| ≤ B_{\rm NF}$ begrenzt, wobei der Index für „Niederfrequenz” steht.
- Der Kanal kann eine elektrische Leitung (Koaxialkabel, Twisted Pair, usw.), ein Lichtwellenleiter (Multimode– bzw. Monomode–Glasfaser) oder eine Funkverbindung (Richtfunk, Satellitenfunk, Mobilfunk, usw.) sein und wird hier durch seinen Frequenzgang $H_{\rm K}(f)$ beschrieben.
- Der mittlere Block in obigem Bild beinhaltet auch Störungen (Interferenzen, Übersprechen anderer Nutzer, Impulsstörungen durch Starkstromleitungen, etc.) und Rauschquellen wie Widerstands– und Halbleiterrauschen. Diese werden durch das Störleistungsdichtespektrum ${\it Φ}_n(f)$ erfasst.
- Aufgabe eines solchen Nachrichtenübertragungssystems ist es, die im Quellensignal $q(t)$ enthaltene Nachricht bzw. Information – man beachte die unterschiedliche Bedeutung dieser zwei Größen – zur räumlich entfernten Sinke zu übertragen mit der Maßgabe, dass sich das Sinkensignal $υ(t)$ „möglichst wenig” von $q(t)$ unterscheidet.
- Ein häufig auftretendes Problem ist, dass der Übertragungskanal für die direkte Übertragung des Quellensignals $q(t)$ ungeeignet ist, da dieses für ihn ungünstige Frequenzen beinhaltet. So kann ein Musiksignal mit Frequenzen bis ca. 15 kHz nicht direkt per Funk übertragen werden, da eine Funkausbreitung erst ab etwa 100 kHz möglich ist.
- Abhilfe schafft hier nur eine Signalumsetzung beim Sender, die man Modulation nennt. Das Ausgangssignal des Modulators wird im Folgenden einheitlich als das Sendesignal $s(t)$ bezeichnet. Dieses liegt im Allgemeinen bei höheren Frequenzen als das Quellensignal $q(t)$.
- Die Demodulation ist die Signalrücksetzung beim Empfänger, um aus dem hochfrequenten Empfangssignal $r(t)$ das niederfrequente Sinkensignal $υ(t) ≈ q(t)$ zu gewinnen. Bei realem Kanal ist aufgrund des stets vorhandenen Rauschens $n(t)$ das Wunschergebnis $υ(t) = q(t)$ nicht möglich.
Anpassung an Übertragungskanal und Störspektrum
Die vorrangige Aufgabe der Modulation (im hier gemeinten Sinne) ist es, das Nachrichtensignal durch Zusetzen eines höherfrequenten Trägersignals mit der Trägerfrequenz $f_{\rm T}$ in eine andere Frequenzlage
- mit günstigerem Frequenzgang $H_{\rm K}(f)$ und/oder
- mit günstigerem Störleistungsdichtespektrum ${\it Φ}_n(f)$
zu verschieben. Weitere Gründe für Modulation/Demodulation werden in den nachfolgenden Abschnitten genannt.
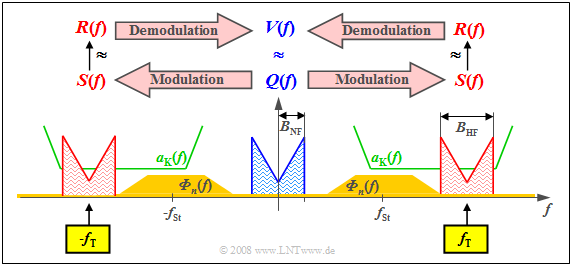
Die Grafik zeigt in blau das niederfrequente Spektrum $Q(f)$ mit der Bandbreite $B_{\rm NF}$. Grün eingezeichnet ist der Dämpfungsverlauf $a_{\rm K}(f) = \ –ln |H_{\rm K}(f)|$ des Kanals, der hier in einem ausreichend großen Frequenzbereich günstige Eigenschaften mit konstant geringer Dämpfung zeigt.
Ockerfarben sehen Sie das Störleistungsdichtespektrum ${\it Φ}_n(f)$, das wegen des thermischen Rauschens im gesamten Frequenzbereich nicht verschwindet und bei unserem konstruierten Beispiel um die Frequenz $f_{\rm St}$ aufgrund äußerer Störungen besonders große Werte annimmt.
Diese Randbedingungen machen deutlich:
- Man muss die Trägerfrequenz $f_{\rm T}$ in etwa so wählen wie eingezeichnet, damit $S(f)$ bestmöglich hinsichtlich Verzerrungen und Störungen/Rauschen übertragen werden kann. Es ergibt sich so ein Frequenzband ausreichender Qualität der Breite $B_{\rm HF} = 2 · B_{\rm NF}$.
- Diese Verschiebung des Quellensignal–Spektrums $Q(f)$ um die Trägerfrequenz $f_{\rm T}$ nach rechts – und aufgrund der systemtheoretischen Betrachtungsweise beidseitiger Frequenzen auch um den gleicen Abstand nach links – beschreibt die Modulation.
- Dagegen versteht man unter Demodulation die Signalumsetzung in Gegenrichtung. Ausgehend vom Empfangsspektrum $R(f)$, das sich vom Sendespektrum $S(f)$ aufgrund von Dämpfung und Rauschen zumindest geringfügig unterscheidet, kommt man zur Spektralfunktion $V(f) ≈ Q(f)$.
Bündelung von Kanälen – Frequenzmultiplex
Ein weiterer Vorteil der Modulation mit einer harmonischen Schwingung als Trägersignal liegt darin, dass ein einziger Übertragungskanal ausreichender Bandbreite von mehreren Teilnehmern gleichzeitig genutzt werden kann. Man spricht dann von Frequenzmultiplex bzw. FDM (Frequency Division Multiplexing) oder auch von FDMA (Frequency Division Multiple Access).
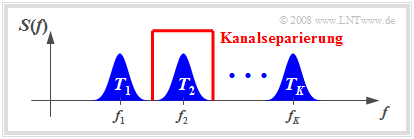
Die Grafik verdeutlicht den Sachverhalt. Über einen physikalischen Kanal entsprechender Bandbreite sollen $K$ Nachrichtensignale gleichzeitig übertragen werden. Die Teilkanäle sind hier mit $T_1, ... , T_K$ bezeichnet. Man geht folgendermaßen vor:
- Man moduliert die Quellensignale $q_1(t), q_2(t), ... , q_K(t)$ der einzelnen Teilnehmer mit den unterschiedlichen Trägerfrequenzen $f_1, f_2, ... , f_K.$
- Man fasst die Signale $s_1(t), s_2(t), ... , s_K(t)$ zu einem Gesamtsignal $s(t)$ zusammen, so dass eine Mehrfachausnutzung der Übertragungseinrichtungen möglich ist.
- Zur Demodulation des Quellensignals $q_k(t)$ verwendet man die spezielle Trägerfrequenz $f_k$. Durch anschließende Filterung erreicht man $υ_k(t) = q_k(t)$. Man nennt den Vorgang Kanalseparierung.
Die Frequenzmultiplextechnik wird schon seit vielen Jahrzehnten in der analogen TV– und Rundfunk–Übertragung angewandt. So können ausreichend viele Programme berücksichtigt werden, zum Beispiel im UHF–Band (470 ... 850 MHz) mehr als vierzig TV–Programme im Kanalabstand von 8 MHz. Seit etwa 2004 wird die analoge TV–Übertragung in diesem Frequenzband allerdings mehr und mehr durch den neuen digitalen Video–Standard DVB–T (Digital Video Broadcast–Terrestrical) verdrängt, der ebenfalls FDMA nutzt.
In der optischen Übertragungstechnik firmiert das gleiche FDMA–Verfahren unter der Bezeichnung Wellenlängenmultiplex bzw. WDM (Wave–length Division Multiplex). Damit können über einen einzigen Lichtwellenleiter derzeit (2005) gleichzeitig 160 Digitalsignale à 10 Gbit/s übertragen werden, was einer Gesamtbitrate von 1.6 Tbit/s entspricht.
Analoge und digitale Modulationsverfahren (1)
Für das gesamte Buch „ Modulationsverfahren” wird vorausgesetzt, dass das Quellensignal $q(t)$ und das Sinkensignal $υ(t)$ jeweils Analogsignale – also sowohl zeitkontinuierlich als auch wertkontinuierlich – seien. Damit ist aber noch nicht festgelegt, ob die eigentliche Übertragung analog oder digital erfolgt.
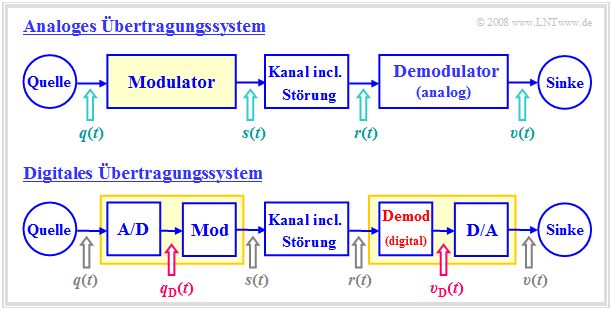
Die beiden Blockschaltbilder verdeutlichen die wesentlichen Unterschiede zwischen einem analogen und einem digitalen Nachrichtenübertragungssystem. Man erkennt:
- Bei analoger Modulation ist das modulierende Signal $q(t)$ immer ein Analogsignal und damit sowohl wert– als auch zeitkontinuierlich.
- Dagegen ist bei digitaler Modulation das Eingangssignal $q_{\rm D}(t)$ des Modulators stets digital, also sowohl wertdiskret als auch zeitdiskret.
- Bei digitaler Modulation eines Audio– oder Videosignals muss $q(t)$ zunächst A/D–gewandelt werden, was folgende Maßnahmen erfordert: Abtastung – Quantisierung – (PCM–)Codierung.
- Während die Modulatoren der beiden Systeme durchaus gleich sein können, unterscheiden sich die Demodulatoren: Der obere liefert das analoge Signal $υ(t)$, der untere das Digitalsignal $υ_{\rm D}(t)$.
- Weiter erkennen wir aus obiger Grafik, dass nach der digitalen Übertragung eines Analogsignals – beispielsweise Audio oder Video – noch eine D/A–Wandlung erfolgen muss.
Analoge und digitale Modulationsverfahren (2)
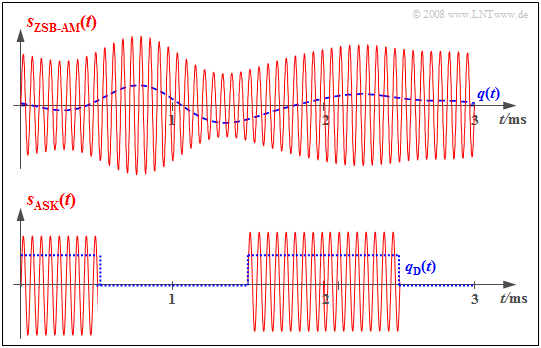
Die beiden Grafiken zeigen die jeweiligen Eingangs– und Ausgangssignale des Modulators bei einem analogen und einem digitalen Übertragungssystem.
Beim System oben steckt die Information über das analoge Quellensignal $q(t)$ direkt in der Amplitude (Hüllkurve) des modulierten Signals $s(t)$. Es handelt sich hierbei um das analoge Modulationsverfahren Zweiseitenband–Amplitudenmodulation mit Träger, das in Kapitel 2.1 beschrieben wird.
Im unteren Bild ist das Modulatoreingangssignal $q_{\rm D}(t)$ digital und aus dem analogen Quellensignal $q(t)$ durch Abtastung, Quantisierung und PCM–Codierung entstanden – siehe Kapitel 4.1. Das modulierte Signal $s(t)$ zeigt, dass der Modulator eine ähnliche Funktionalität aufweist wie im oberen Beispiel. Man bezeichnet diese digitale Variante der Amplitudenmodulation als ASK (Amplitude Shift Keying).
Analoge Modulationsverfahren haben derzeit (2005) vor allem für die Verbreitung von Rundfunk– und Fernsehprogrammen noch eine gewisse Bedeutung, werden aber auch in diesem Bereich mehr und mehr durch entsprechende Digitalverfahren verdrängt. Trotzdem nehmen die Analogverfahren in diesem Buch einen breiteren Raum – Kapitel 2 und Kapitel 3 – ein. Die Gründe hierfür sind:
- Aufgrund der hohen Kosten bei der Umrüstung bestehender sowie der Einführung neuer Systeme werden auch für die Analogsysteme noch längere Laufzeiten prognostiziert.
- Viele Komponenten eines Analogsystems werden ebenso bei den digitalen Modulationsverfahren benötigt, zum Beispiel der in beiden Varianten verwendete Synchrondemodulator.
- Die typische Vorgehensweise bei der Untersuchung nachrichtentechnischer Aspekte lässt sich bei Analogsystemen umfassender – und oft auch verständlicher – erklären als bei Digitalsystemen.
Bevor wir uns den digitalen Modulationsverfahren zuwenden, folgen einige Daten zur geschichtlichen Entwicklung der analogen Modulation.