Allgemeines Modell der Modulation

1. Modulationsverfahren
2. Allgemeine Beschreibung
3. Allgemeines Modell der Modulation

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Gemeinsame Beschreibung von Amplituden– und Winkelmodulation

Bei den Beschreibungen von

• Amplitudenmodulation ⇒ Kapitel 2, und
• Winkelmodulation ⇒ Kapitel 3

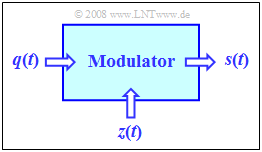
wird stets die nebenstehende Konstellation betrachtet. Der zentrale Block ist hierbei der Modulator.

Die beiden Eingangssignale und das Ausgangssignal weisen folgende Eigenschaften auf:

• Das Quellensignal $q(t)$ ist das niederfrequente Nachrichtensignal und besitzt das Spektrum $Q(f)$. Dieses Signal ist wert– und zeitkontinuierlich und auf den Frequenzbereich $|f| ≤ B_{\rm NF}$ begrenzt.
• Das Trägersignal $z(t)$ ist eine harmonische Schwingung der Form

$$z(t) = A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t - \varphi_{\rm T})= A_{\rm T} \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})\hspace{0.05cm}.$$

Dieses deterministische Signal ist durch die Amplitude $A_{\rm T}$, die Frequenz $f_{\rm T}$ und die Nullphasenlage ${\it ϕ}_{\rm T}$ beschreibbar. Während bei Anwendung von Fourierreihe und Fourierintegral meist die linke Gleichung mit Minuszeichen und $φ_{\rm T}$ benutzt wird, ist zur Beschreibung der Modulationsverfahren die rechte Gleichung mit ${\it ϕ}_{\rm T} = – φ_{\rm T}$ und Pluszeichen üblich.

• Das Sendesignal $s(t)$ ist ein hochfrequentes Signal, dessen Spektralfunktion $S(f)$ im Bereich um die Trägerfrequenz $f_{\rm T}$ liegt. Dieses Modulatorausgangssignal hängt von beiden Eingangssignalen $q(t)$ und $z(t)$ ab. Die nachfolgend betrachteten Modulationsverfahren differieren ausschließlich durch unterschiedliche Verknüpfungen von $q(t)$ und $z(t)$.

Eine sehr einfache, leider nicht ganz richtige Modulatorgleichung

Ausgehend von der harmonischen Schwingung (hier mit der Kreisfrequenz $ω_{\rm T} = 2πf_{\rm T}$ geschrieben) $$z(t) = A_{\rm T} \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T})$$ kommt man zur allgemeinen Modulatorgleichung, indem die bisher festen Schwingungsparameter als zeitabhängig angesetzt werden: $$s(t) = a(t) \cdot \cos(\omega(t) \cdot t + \phi(t))\hspace{0.05cm}.$$ !! Vorsicht !! Diese allgemeine Modulatorgleichung ist sehr einfach und plakativ und trägt zum Verständnis der Modulationsverfahren bei. Leider stimmt diese Gleichung bei der Frequenzmodulation nur in Ausnahmefällen. Hierauf wird in Kapitel 3.2 noch ausführlich eingegangen.

Als Sonderfälle sind in dieser Gleichung enthalten:

• Bei der Amplitudenmodulation (AM) ändert sich die zeitabhängige Amplitude entsprechend dem Quellensignal, während die beiden anderen Signalparameter konstant sind:

$$\omega(t) = \omega_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm}\phi(t) = \phi_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm} a(t) = {\rm Funktion \hspace{0.15cm}von}\hspace{0.15cm}q(t) .$$

• Bei der Frequenzmodulation (FM) wird ausschließlich die momentane (Kreis–)Frequenz durch das Quellensignal bestimmt:

$$a(t) = A_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm}\phi(t) = \phi_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm} \omega(t) = {\rm Funktion \hspace{0.15cm}von}\hspace{0.15cm}q(t) .$$

• Bei der Phasenmodulation (PM) variiert die Phase entsprechend dem Quellensignal:

$$a(t) = A_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm}\omega(t) = \omega_{\rm T} = {\rm const.}\hspace{0.08cm}, \hspace{0.2cm} \phi(t) = {\rm Funktion \hspace{0.15cm}von}\hspace{0.15cm}q(t) .$$

Bei diesen grundlegenden Verfahren werden also stets zwei der drei Schwingungsparameter konstant gehalten. Daneben gibt es auch Varianten mit mehr als einer Zeitabhängigkeit von Amplitude, Frequenz bzw. Phase. Ein Beispiel hierfür ist die Einseitenbandmodulation (siehe Kapitel 2.4), bei der sowohl $a(t)$ als auch ${\it ϕ}(t)$ vom Quellensignal $q(t)$ beeinflusst werden.

Modulierte Signale bei digitalem Quellensignal

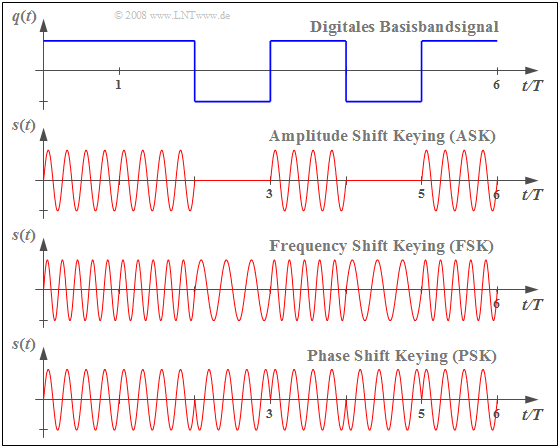
Die Grafik zeigt ein rechteckförmiges Quellensignal $q(t)$ und die modulierten Signale $s(t)$, die sich bei den eben vorgestellten Modulationsverfahren ergeben.

• Bei der Amplitudenmodulation, deren digitale Variante unter der Bezeichnung ASK (Amplitude Shift Keying) bekannt ist, ist das Nachrichtensignal in der Hüllkurve von $s(t)$ zu erkennen.
• Im Signalverlauf der FSK (Frequency Shift Keying) werden die beiden möglichen Signalwerte von $q(t) =$ +1 bzw. $q(t) =$ –1 durch zwei unterschiedliche Frequenzen dargestellt.
• Dagegen führt die PSK (Phase Shift Keying) bei den Amplitudensprüngen des Quellensignals $q(t)$ zu Phasensprüngen im Signal $s(t)$, im binären Fall jeweils um $\pm π$ (bzw. $\pm$180°).

Beschreibung von $s(t)$ mit Hilfe des analytischen Signals (1)

Das modulierte Signal $s(t)$ ist bandpassartig. Wie bereits im Kapitel 4.2 des Buches „Signaldarstellung” beschrieben wurde, wird ein solches BP–Signal $s(t)$ häufig durch das dazugehörige analytische Signal $s_+(t)$ charakterisiert. Zu beachten ist:

• Das analytische Signal $s_+(t)$ erhält man aus dem reellen, physikalischen Signal $s(t)$, indem zu diesem als Imaginärteil dessen Hilberttransformierte hinzugefügt wird:

$$s_+(t) = s(t) + {\rm j} \cdot {\rm H}\{ s(t)\}\hspace{0.05cm}.$$

• Das analytische Signal $s_+(t)$ ist somit stets komplex. Zwischen den beiden Zeitsignalen gilt der folgende einfache Zusammenhang:

$$s(t) = {\rm Re} [s_+(t)] \hspace{0.05cm}.$$

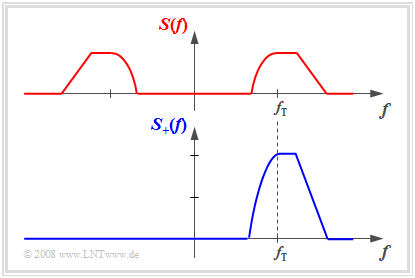
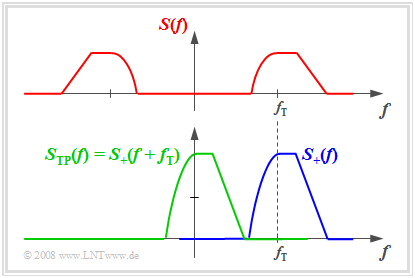
• Das Spektrum $S_+(f)$ des analytischen Signals ergibt sich aus $S(f)$, wenn man dieses bei positiven Frequenzen verdoppelt und für negative Frequenzen zu Null setzt:

$$S_+(f) =\left[ 1 + {\rm sign}(f)\right] \cdot S(f) = \left\{ \begin{array}{c} 2 \cdot S(f) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} f>0 \hspace{0.05cm}, \\ f<0 \hspace{0.05cm}, \\ \end{array}$$

mit

$${\rm sign}(f) = \left\{ \begin{array}{c} +1 \\ -1 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} f>0 \hspace{0.05cm}, \\ f<0 \hspace{0.05cm}. \\ \end{array}$$

Die nachfolgende Grafik verdeutlicht diesen Zusammenhang an einem Beispiel:

Der hier dargelegte Sachverhalt wird mit nachfolgend genanntem Interaktionsmodul verdeutlicht:

Zeigerdiagramm – Darstellung des analytischen Signals

Beschreibung von $s(t)$ mit Hilfe des analytischen Signals (2)

Wenden wir nun diese Definitionen auf das modulierte Signal $s(t)$ an. Im Sonderfall $q(t) =$ 0 ist $s(t)$ wie das Trägersignal $z(t)$ eine harmonische Schwingung, und es gilt: $$s(t) = A_{\rm T} \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T}) \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} s_+(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm}(\omega_{\rm T}\hspace{0.05cm} t \hspace{0.05cm} + \phi_{\rm T})}\hspace{0.05cm}.$$

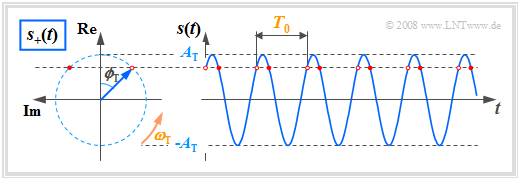
Die zweite Gleichung beschreibt einen Drehzeiger mit folgenden Eigenschaften:

• Die Zeigerlänge kennzeichnet die Signalamplitude $A_{\rm T}$.
• Zur Zeit $t =$ 0 liegt der Zeiger mit dem Winkel $ϕ_{\rm T}$ in der komplexen Ebene.
• Für $t$ > 0 dreht der Zeiger mit der konstanten Winkelgeschwindigkeit $ω_{\rm T}$ in mathematisch positive Richtung, also entgegen dem Uhrzeigersinn.
• Die Zeigerspitze liegt stets auf einem Kreis mit dem Radius $A_{\rm T}$ und benötigt für eine Umdrehung genau die Periodendauer $T_0$.

Die Grafik gilt für $ϕ_{\rm T} =$ –45°. Um den Zusammenhang $s(t) = {\rm Re}[s_+(t)]$ im Querformat verdeutlichen zu können, ist die komplexe Ebene entgegen der üblichen Darstellung um 90° nach links gedreht: Der Realteil ist nach oben und der Imaginärteil nach links aufgetragen.

Die einzelnen Modulationsverfahren lassen sich nun wie folgt darstellen:

• Bei der Amplitudenmodulation ändert sich die Zeigerlänge $a(t) = |s_+(t)|$ und damit die Hüllkurve von $s(t)$ entsprechend dem Quellensignal $q(t)$. Die Winkelgeschwindigkeit $ω(t)$ ist dabei konstant.
• Bei der Frequenzmodulation ändert sich die Winkelgeschwindigkeit $ω(t)$ des rotierenden Zeigers entsprechend $q(t)$, während die Zeigerlänge $a(t) = A_{\rm T}$ nicht verändert wird.
• Bei der Phasenmodulation ist die Phase $ϕ(t)$ zeitabhängig. Es bestehen viele Gemeinsamkeiten mit der Frequenzmodulation, die ebenfalls eine Winkelmodulation ist.

Beschreibung von $s(t)$ mit Hilfe des äquivalenten TP-Signals (1)

Manche Sachverhalte bezüglich der sendeseitigen Modulation und der Demodulation am Empfänger lassen sich anhand des äquivalenten Tiefpass–Signals anschaulich erklären, das bereits im Kapitel 4.3 des Buches „Signaldarstellung” definiert wurde.

Für dieses Signal $s_{\rm TP}(t)$ und dessen Spektrum $S_{\rm TP}(f)$ gelten die folgenden Aussagen:

• Das Spektrum $S_{\rm TP}(f)$ des äquivalenten Tiefpass–Signals erhält man aus $S_+(f)$ durch Verschiebung um $f_{\rm T}$ nach links:

$$S_{\rm TP}(f) = S_+(f + f_{\rm T}) \hspace{0.05cm}.$$

Aus der Grafik erkennt man, dass $S_{\rm TP}(f)$ im Bereich um die Frequenz $f =$ 0 liegt.

• Nach dem Verschiebungssatz gilt somit für die zugehörige Zeitfunktion:

$$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{{-\rm j}\hspace{0.08cm} \omega_{\rm T} \hspace{0.03cm}t }\hspace{0.05cm}.$$

Den zeitabhängigen Verlauf von $s_{\rm TP}(t)$ in der komplexen Ebene bezeichnen wir im Folgenden als Ortskurve, während das Zeigerdiagramm den Verlauf des analytischen Signals $s_+(t)$ beschreibt.

• Das äquivalente Tiefpass–Signal einer unmodulierten harmonischen Schwingung ist für alle Zeiten konstant – die Ortskurve besteht in diesem Sonderfall aus einem einzigen Punkt:

$$s(t) = A_{\rm T} \cdot \cos(\omega_{\rm T}\cdot t + \phi_{\rm T}) \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} s_+(t) = {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm}(\omega_{\rm T}\hspace{0.05cm} t \hspace{0.05cm} + \phi_{\rm T})}\hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} s_{\rm TP}(t) = A_{\rm T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.05cm} \phi_{\rm T}}\hspace{0.05cm}.$$

• Dagegen gilt für ein amplituden– oder phasenmoduliertes Signal mit der Trägerfrequenz $f_{\rm T}$:

$$s(t) = a(t) \cdot \cos(\omega_{\rm T}\cdot t + \phi(t)) \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} s_{\rm TP}(t) = a(t) \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.05cm} \phi (t)}\hspace{0.05cm}.$$

Das bedeutet: Die Hüllkurve $a(t)$ und der Phasenverlauf $ϕ(t)$ des Bandpass-Signals $s(t)$ bleiben auch im äquivalenten TP–Signal $s_{\rm TP}(t)$ erhalten.

Die hier erläuterten Zusammenhänge können Sie sich mit folgendem Interaktionsmodul verdeutlichen:

Ortskurve – Verlauf des äquivalenten Tiefpass-Signals

Beschreibung von $s(t)$ mit Hilfe des äquivalenten TP-Signals (2)

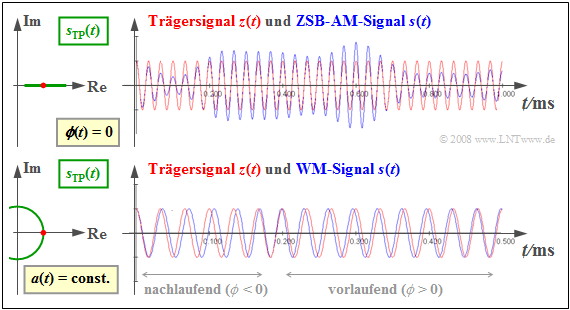
Die Grafik zeigt jeweils rechts das modulierte Signal $s(t)$ ⇒ roter Signalverlauf im Vergleich zum Trägersignal $z(t)$ ⇒ blauer Signalverlauf. Links dargestellt sind die jeweiligen äquivalenten Tiefpass–Signale $s_{\rm TP}(t)$ ⇒ grüne Ortskurven.

Die obere Skizze beschreibt die Amplitudenmodulation, bei der das Quellensignal $q(t)$ in der Hüllkurve $a(t)$ zu erkennen ist. Da die Nulldurchgänge von $z(t)$ in $s(t)$ erhalten bleiben, ist $ϕ(t) =$ 0 und das äquivalente TP–Signal $s_{\rm TP}(t) = a(t)$ reell. Die Herleitung dieses Sachverhalts erfolgt im Kapitel 2.3.

Dagegen ist bei Winkelmodulation die Hüllkurve $a(t)$ konstant, so dass hier das äquivalente TP-Signal $s_{\rm TP}(t) = A_{\rm T} · e^{{\rm j}·ϕ(t)}$ einen Kreisbogen beschreibt. Die Information über das Nachrichtensignal steckt nun in der Lage der Nulldurchgänge von $s(t)$. Genaueres hierüber finden Sie im Kapitel 3.1.