Aufgabe 1.1: Einfache Filterfunktionen

• Zurück zum Buch

A1.1 Einfache Filterfunktionen

Man bezeichnet ein Filter mit dem Frequenzgang $$H_{\rm TP}(f) = \frac{1}{1+ {\rm j}\cdot f/f_0}$$ als Tiefpass erster Ordnung. Daraus lässt sich ein Hochpass erster Ordnung nach folgender Vorschrift gestalten: $$H_{\rm HP}(f) = 1- H_{\rm TP}(f) .$$

In beiden Fällen gibt $f_0$ die so genannte 3dB–Grenzfrequenz an.

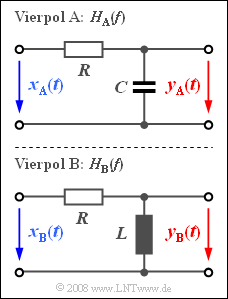
Die Abbildung zeigt zwei Vierpole A und B. In der Aufgabe ist zu klären, welcher der beiden Vierpole eine Tiefpass– und welcher eine Hochpasscharakteristik aufweist.

Die Bauelemente von Schaltung A sind wie folgt gegeben: $$R = 50 \,\, {\rm \Omega}; \hspace{0.1cm} C = 0.637 \,\, {\rm \mu F} .$$

Die Induktivität $L$ ist in der Teilaufgabe f) zu berechnen.

Für die Teilaufgabe d) wird vorausgesetzt, dass die Eingangssignale cosinusförmig seien. Die Frequenz $f_x$ ist variabel, die Leistung beträgt jeweils $P_x =$ 10 mW.

Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.1.

Fragebogen zu "A1.1 Einfache Filterfunktionen"

1

Berechnen Sie den Frequenzgang $H_{\rm A}(f)$ des Vierpols A und beantworten Sie folgende Fragen.

	Vierpol A ist ein Tiefpass.
	Vierpol A ist ein Hochpass.

2

Berechnen Sie die Bezugsfrequenz $f_0$ aus den Bauelementen $R$ und $C$.

$f_0$ = kHz

3

Berechnen Sie den Amplitudengang $|H_{\rm A}(f)|$. Welche Zahlenwerte ergeben sich für $f = f_0$ und $f = 2f_0$?

$|H_{\rm A}(f = f_0)|$ =

$|H_{\rm A}(f = 2f_0)|$ =

4

Wie groß ist die Leistung $P_y$ des Ausgangssignals $y(t)$, wenn am Eingang ein Cosinussignal mit den Frequenzen $f_x =$ 5 kHz bzw. $f_x =$ 10 kHz anliegt?

$P_y(f_x = 5 kHz)$ = mW

$P_y(f_x = 10 kHz)$ = mW

5

Berechnen Sie den Amplitudengang $|H_{\rm B}(f)|$ des Vierpols mit den Elementen $R$ und $L$ unter Verwendung der Bezugsfrequenz $f_0 = R/(2πL)$. Welche Werte ergeben sich für $f =$ 0, $f = f_0% und %f = 2f_0$ sowie für $f → ∞$?

$|H_{\rm B}(f = 0)|$ =

$|H_{\rm B}(f = f_0)|$ =

$|H_{\rm B}(f = 2f_0)|$ =

$|H_{\rm B}(f → ∞)|$ =

6

Welche Induktivität führt zu der Bezugsfrequenz $f_0 =$ 5 kHz?

$L$ = mH

Musterlösung

Musterlösung

a) Der komplexe Widerstand der Kapazität $C$ ist gleich $1/({\rm j}ωC)$, wobei $ω = 2πf$ die so genannte Kreisfrequenz angibt. Der Frequenzgang lässt sich nach dem Spannungsteilerprinzip berechnen:

$$H_{\rm A}(f) = \frac{Y_{\rm A}(f)}{X_{\rm A}(f)} = \frac{1/({\rm j}\omega C)}{R+1/({\rm j}\omega C)}=\frac{1}{1+{\rm j \cdot 2\pi}\cdot f \cdot R\cdot C}.$$ Wegen $H_{\rm A}(f = 0) = 1$ kann dies kein Hochpass sein; vielmehr handelt es sich um einen Tiefpass. Bei niedrigen Frequenzen ist der Blindwiderstand der Kapazität sehr groß und es gilt $y_{\rm A}(t) ≈ x_{\rm A}(t)$. Dagegen wirkt der Kondensator bei sehr hohen Frequenzen wie ein Kurzschluss und es ist $y_{\rm A}(t) ≈ 0$.

b)

c)

d)

e)

f)

g)