Aufgabe 1.4Z: Alles rechteckförmig

• Zurück zum Buch

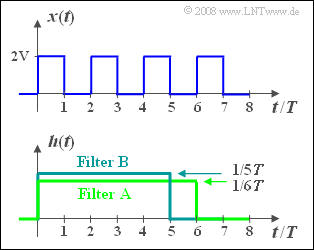
Wir betrachten das periodische Rechtecksignal $x(t)$ gemäß obiger Skizze, dessen Periodendauer $T_0 = 2T$ ist. Dieses Signal besitzt Spektralanteile bei der Grundfrequenz $f_0 = 1/T_0 = 1/(2T)$ und allen ungeradzahligen Vielfachen davon, d.h. bei $3f_0, 5f_0,$ usw. Zusätzlich gibt es einen Gleichanteil.

Dazu betrachten wir zwei Filter A und B mit jeweils rechteckförmiger Impulsantwort $h_{\rm A}(t)$ mit Dauer $6T$ bzw. $h_{\rm B}(t)$ mit der Dauer $5T$. Die Höhen der beiden Impulsantworten sind so gewählt, dass die Flächen der Rechtecke jeweils 1 ergeben.

Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.2. Informationen zur Faltung finden Sie im Kapitel 3.4 des Buches „Signaldarstellung”.

Fragebogen

1

Berechnen Sie das Ausgangssignal $y_{\rm A}(t)$ von Filter A, insbesondere die Werte bei $t = 0$ und $t = T$.

$y_{\rm A}(t = 0) =$ V

$y_{\rm A}(t = T) =$ V

2

Geben Sie die Betragsfunktion $|H_{\rm A}(f)|$ an. Welcher Wert ergibt sich bei der Frequenz $f = f_0$? Interpretieren Sie das Ergebnis der Teilaufgabe 1).

$|H_{\rm A}(f = f_0)| =$

3

Berechnen Sie das Ausgangssignal $y_{\rm B}(t)$ von Filter B, insbesondere die Werte bei $t = 0$ und $t = T$.

$y_{\rm B}(t = 0) =$ V

$y_{\rm B}(t = T) =$ V

4

Wie lautet die Betragsfunktion $|H_{\rm B}(f)|$, insbesondere bei den Frequenzen $f = f_0$ und $f = 3 · f_0$? Interpretieren Sie damit das Ergebnis von 3).

$|H_{\rm B}(f = f_0)| =$

$|H_{\rm B}(f = 3f_0)| =$

Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.