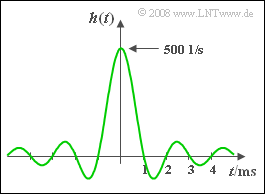
Aufgabe 1.5Z: si-förmige Impulsantwort
Die Impulsantwort eines linearen zeitinvarianten (und akausalen) Systems wurde wie folgt ermittelt (siehe Grafik): $$h(t) = 500\hspace{0.05cm}\frac{1}{ {\rm s}}\cdot{\rm si}(\pi \cdot \frac{t}{ 1\hspace{0.1cm}{\rm ms}}) .$$ Berechnet werden sollen die Ausgangssignale $y(t)$, wenn am Eingang verschiedene Cosinusschwingungen unterschiedlicher Frequenz $f_0$ angelegt werden: $$x(t) = 4\hspace{0.05cm}{\rm V}\cdot {\rm cos}(2\pi \cdot f_0 \cdot t ) .$$ Die Lösung kann entweder im Zeitbereich oder auch im Frequenzbereich gefunden werden. In der Musterlösung werden jeweils beide Lösungswege angegeben. Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 1.3. Gegeben ist dazu das folgende bestimmte Integral: $$\int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u = \left\{ \begin{array}{c} \pi/2 \\ \pi/4 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{ |a| < 1,} \\{ |a| = 1,} \\ { |a| > 1.} \\ \end{array}$$
Fragebogen
Musterlösung