Aufgabe 1.4: 2S/3E-Kanalmodell

• Zurück zum Buch

Ein Sender gibt die binären Symbole $L$ (Ereignis $S_L$) und $H$ (Ereignis $S_H$) ab. Bei guten Bedingungen entscheidet sich der Digitalempfänger ebenfalls nur für die Binärsymbole $L$ (Ereignis $E_L$) oder $H$ (Ereignis $E_H$). Kann der Empfänger allerdings vermuten, dass bei der Übertragung ein Fehler aufgetreten ist, so trifft er keine Entscheidung (Ereignis $E_K$; $K$ steht dabei für „Keine Entscheidung”).

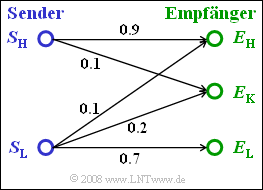
Die Grafik zeigt ein einfaches Kanalmodell in Form von Übergangswahrscheinlichkeiten. Es ist zu erkennen, dass ein gesendetes $L$ durchaus als Symbol $H$ empfangen werden kann. Dagegen ist der Übergang von $H$ nach $L$ nicht möglich.

Die Symbolauftrittswahrscheinlichkeiten am Sender seien $Pr(S_L)$ = 0.3 und $Pr(S_H)$ = 0.7.

Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 1.3. Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:

Fragebogen

1

Wie groß ist die Wahrscheinlichkeit dafür, dass sich der Empfänger für das Symbol $L$ entscheidet?

$Pr(E_L)$ =

2

Wie groß ist die Wahrscheinlichkeit dafür, dass sich der Empfänger für das Symbol $H$ entscheidet?

$Pr(E_H)$ =

3

Wie groß ist die Wahrscheinlichkeit dafür, dass der Empfänger keine Entscheidung trifft?

$Pr(E_K)$ = { 0.13 3%}

4

Mit welcher Wahrscheinlichkeit entscheidet der Empfänger falsch?

$Pr(falsche Entscheidung)$ =

5

Wie groß ist die Wahrscheinlichkeit, dass das Symbol $L$ gesendet wurde, wenn sich der Empfänger für das Symbol $L$ entschieden hat?

$Pr(S_L|E_L)$ =

6

Wie groß ist die Wahrscheinlichkeit, dass das Symbol $L$ gesendet wurde, wenn der Empfänger keine Entscheidung trifft?

$Pr(S_L|E_K)$ =

Musterlösung

Musterlösung

1. 2. 3. 4. 5. 6. 7.