Aufgabe 1.5Z: Ausfallwahrscheinlichkeiten

• Zurück zum Buch

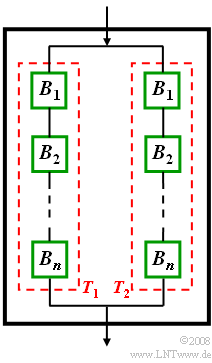
Ein Geräteteil ist aus den Bauteilen $B1, B2,…, Bn$ aufgebaut, wobei die jeweilige Funktionsfähigkeit unabhängig von allen anderen angenommen werden kann. Das Teil $T_1$ funktioniert nur dann, wenn alle $n$ Bauteile funktionsfähig sind. Gehen Sie davon aus, dass alle Bauteile mit gleicher Wahrscheinlichkeit $p_A$ ausfallen.

Zur Erhöhung der Zuverlässigkeit werden wichtige Baugruppen häufig dupliziert. Das Gerät $G$ kann somit mengentheoretisch wie folgt beschrieben werden: $$ G = T_1 \cup T_2 $$

Das heißt: Das Gerät $G$ ist bereits dann einsatzbereit, wenn zumindest eines der beiden baugleichen Teilgeräte ($T_1$ oder $T_2$) funktionsfähig ist.

Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 1.3. Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:

Fragebogen

1

Die Ausfallwahrscheinlichkeit $p_G$ des Gesamtgeräts darf nicht größer sein als 0.04%. Wie groß dürfen dann die Ausfallwahrscheinlichkeiten $p_T$ der zwei parallel vorhandenen Geräteteile höchstens sein?

$p_\T,max$ =

2

Die Ausfallwahrscheinlichkeit aller Bauteile sei $p_A = 0.1$. Jedes Teilgerät bestehe aus $n = 3$ Bauteilen. Berechnen Sie die Wahrscheinlichkeit $p_T$ exakt, dass ein Teilgerät ausfällt.

$p_T$ =

3

Welcher Wert ergibt sich für $p_A = 0.01$? In welcher Form kann man $p_T$ für kleine Werte von $p_A$ annähern?

$p_T$ =

4

Nun gelte für die Ausfallwahrscheinlichkeit aller Bauteile $p_A = 0.4%$. Wieviele Bauteile kann das Teilgerät höchstens enthalten, wenn $p_T ≤ 2%$ gelten soll?

$n$ =

Musterlösung

Musterlösung

a)

b)

c)

d)

e)

f)

g)