Aufgabe 1.6Z: Ergodische Wahrscheinlichkeiten

• Zurück zum Buch

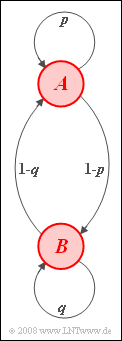
Wir betrachten eine homogene stationäre Markovkette erster Ordnung mit den Ereignissen $A$ und $B$ und den Übergangswahrscheinlichkeiten entsprechend dem nebenstehenden Markovdiagramm:

Für die Teilaufgaben a) bis d) wird vorausgesetzt:

• Nach dem Ereignis $A$ folgen $A$ und $B$ mit gleicher Wahrscheinlichkeit.

• Nach $B$ ist das Ereignis $A$ doppelt so wahrscheinlich wie $B$.

Ab Teilaufgabe e) sind p und q als freie Parameter zu verstehen, während die Ereigniswahrscheinlichkeiten $Pr(A) = 2/3$ und $Pr(B) = 1/3$ vorgegeben sind.

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.4. Zur Ergebniskontrolle können Sie das folgende Berechnungstool nutzen:

Fragebogen

1

Wie groß sind die Übergangswahrscheinlichkeiten $p$ und $q$?

$p$ =

$q$ =

2

Berechnen Sie die ergodischen Wahrscheinlichkeiten.

$Pr(A)$ =

$Pr(B)$ =

3

Wie groß ist die bedingte Wahrscheinlichkeit, dass das Ereignis $B$ auftritt, wenn zwei Takte vorher das Ereignis $A$ aufgetreten ist?

$Pr(B_v|A_\text{v-2})$ =

4

Wie groß ist die Rückschlusswahrscheinlichkeit, dass zwei Takte vorher das Ereignis $A$ aufgetreten ist, wenn aktuell $B$ auftritt?

$Pr(A_\text{v-2}|B_v)$ =

5

Es gelte nun $p = 1/2$ und $Pr(A) = 2/3$. Welcher Wert ergibt sich für $q$?

$q$ =

6

Wie müssen die Parameter gewählt werden, damit die Folgenelemente der Markovkette statistisch unabhängig sind und zusätzlich $Pr(A) = 2/3$ gilt?

$p$ =

$q$ =

Musterlösung

Musterlösung

a)

b)

c)

d)

e)

f)

g)