Aufgabe 3.5: Dreieck- und Trapezsignal

• Zurück zum Buch

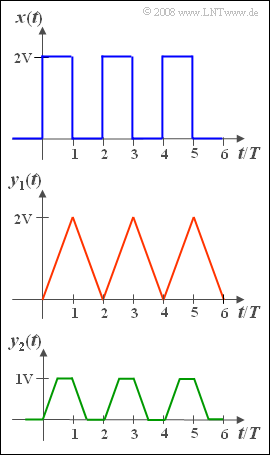
Wir gehen vom Rechtecksignal x(t) gemäß dem oberen Bild aus. Die Amplitudenwerte sind 0V und 2V, die Dauer eines Rechtecks sowie der Abstand zweier aufeinander folgender Rechteckimpulse seien jeweils gleich T. Die Zufallsgröße x – der Momentanwert des Rechtecksignals x(t) – hat somit folgende Kennwerte: m_x = σ_x = 1V.

Gibt man nun dieses Signal auf ein lineares Filter mit der Impulsantwort

$$\it h_{\rm 1}(\it t)=\left \{ \begin{array}{*{4}{c}} 1/\it T & \rm f\ddot{u}r\hspace{0.1cm}{\rm 0\le \it t \le \rm \it T} \\\rm 0 & \rm sonst \end{array} \right. , $$

so ergibt sich an dessem Ausgang entsprechend der Faltung das Dreiecksignal y₁(t) = x(t) * h₁(t) mit

• den Minimalwerten 0V (bei t = 0, 2T, 4T, ...),

• den Maximalwerten 2V (bei t = T, 3T, 5T, ...).

Bei diesem Tiefpassfilter handelt es sich also um einen Integrator über die Zeitdauer T.

Legt man dagegen das Rechtecksignal x(t) an den Eingang eines Filters mit der Impulsantwort

$$\it h_{\rm 2}(\it t)=\left\{ \begin{array}{*{4}{c}} 1/ \it T & \rm f\ddot{u}r\hspace{0.1cm}{\rm 0\le \it t \le \rm \it T{\rm /2}} \\\rm 0 & \rm sonst \end{array} \right. ,$$

so ergibt sich das unten dargestellte trapezförmige Signal y₂(t) = x(t) * h₂(t). Dieses zweite Filter wirkt somit als ein Integrator über die Zeitdauer T/2.

Anzumerken ist, dass für die zugehörigen Frequenzgänge H₁(f = 0) = 1 bzw. H₂(f = 0) = 0.5 gilt.

Hinweis: Diese Aufgabe bezieht sich auf den gesamten Lehrstoff von Kapitel 3.4.

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	y1 ist eine kontinuierliche Zufallsgröße.
	y1 besitzt eine dreieckförmige WDF.
	y1 ist gleichverteilt.
	y2 hat kontinuierliche und diskrete Anteile.

2

Wie groß ist der Gleichanteil des Signals y₁(t)? Überprüfen Sie diesen Wert auch anhand der Größen m_x und H₁(f = 0).

$m_\text{y1}$ = V

3

Bestimmen Sie die Leistung des Signals y₁(t) durch Zeitmittelung.

$P_\text{y1}$ = V^2

4

Berechnen Sie die Leistung P_y1 auch aus der hier vorliegenden WDF. Wie groß ist der Effektivwert des Signals y₁(t)?

$\sigma_\text{y1}$ = V

5

Wie groß ist die Wahrscheinlichkeit, dass y₁(t) größer als 0.75 V ist?

$Pr(y_1\ >\ 0.75V)$ =

6

Ermitteln Sie die WDF des Signals y₂(t) und skizzieren Sie diese. Geben Sie zur Kontrolle den WDF-Wert an der Stelle y₂ = 0.5 V ein.

$f_\text{y2}(y_2\ =\ 0.5V)$ = 1/V

7

Wie groß ist der Gleichanteil des Signals y₂(t)? Überprüfen Sie diesen Wert anhand der Größen m_x und H₂(f = 0).

$m_\text{y2}$ = V

8

Wie groß ist der Effektivwert des Signals y₂(t)?

$\sigma_\text{y2}$ = V

9

Wie groß ist die Wahrscheinlichkeit, dass y₂(t) größer als 0.75 V ist?

$Pr(y2\ >\ 0.75V)$ =

Musterlösung

Musterlösung

1.  Die Zufallsgröße y₁ ist gleichverteilt und dadurch natürlich auch eine kontinuierliche Zufallsgröße. Die WDF von y₂ weist diskrete Anteile bei 0 V und 1 V auf. Zwischen diesen zwei Begrenzungen gibt es selbstverständlich auch kontinuierliche Anteile. In diesem Bereich gilt f_x(x) = 1/2. Richtig sind somit die Lösungsvorschläge 1, 3 und 4.

2.  Der lineare Mittelwert m_y1 = 1V ist aus der Angabenskizze direkt abzulesen, könnte aber auch formal mit der Gleichung für die Gleichverteilung (zwischen 0 V und 2 V) berechnet werden. Eine weitere Lösungsmöglichkeit bietet die Beziehung:

$$m_{y_{\rm 1}}=m_x\cdot H_{\rm 1}(\it f=\rm 0) = \rm 1\,V \cdot 1\hspace{0.15cm}\underline{ =\rm 1\,V}.$$

3.  Eigentlich müsste die Mittelung über den gesamten Zeitbereich (beidseitig bis ins Unendliche) erfolgen. Aus Symmetriegründen genügt jedoch die Mittelung über das Zeitintervall 0 ≤ t ≤ T:

$$P_{y_{\rm 1}}=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}\it y_{\rm 1}(\it t)^{\rm 2}\it \hspace{0.05cm}\hspace{0.1cm}{\rm d}t=\rm\frac{1}{\it T}\cdot \int_{\rm 0}^{\it T} \hspace{-0.15cm}(\rm 2V \cdot \it\frac{t}{T})^{\rm 2} \hspace{0.1cm}{\rm d} t = \rm {4}/{3}\, V^2 \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$

4.  Die Scharmittelung liefert das gleiche Ergebnis. Mit der WDF f_y1(y₁) = 1/(2V) gilt nämlich:

$$P_{y_{\rm 1}}= \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\cdot f_{\it y_{\rm 1}}(\it y_{\rm 1})\it \hspace{0.1cm}{\rm d}y_{\rm 1} =\rm\frac{1}{2V}\cdot \int_0^{2V} \hspace{-0.3cm}\it y_{\rm 1}^{\rm 2}\hspace{0.1cm}{\rm d}y_{\rm 1} =\rm \frac{8\,{\rm V^3}}{3 \cdot 2\,{\rm V}} \hspace{0.15cm}\underline{= \rm 1.333\, V^2}.$$

Die Varianz kann mit dem Satz von Steiner ermittelt werden und ergibt 4/3 V² - 1 V² = 1/3 V². Die Wurzel daraus ist die gesuchte Streuung (der Effektivwert):

$$\sigma_{y_{\rm 1}}\hspace{0.15cm}\underline{=0.577 \, \rm V}.$$

5.  Die gesuchte Wahrscheinlichkeit ist das Integral über die WDF von 0.75V bis 2V, also 0.625.

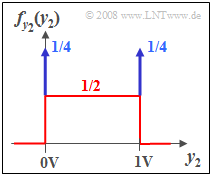
6.  Die WDF besteht aus zwei Diracfunktionen bei 0 V und 1 V (jeweils mit dem Gewicht 1/4) und einem konstanten kontinuierlichen Anteil von 0.5 (mal 1/V). Bei y₂ = 0.5 V gibt es deshalb nur den kontinuierlichen Anteil.

7.  Der Mittelwert m_y2 = 0.5V kann direkt aus obiger WDF-Skizze abgelesen werden oder – wie bei b) – über die Beziehung m_y2 = m_x · H₂ (f = 0) = 1 V · 0.5 berechnet werden.

8.  Mit obiger WDF gilt für die Leistung:

$$P_{y_{\rm 2}}=\int_{-\infty}^{+\infty}\hspace{-0.3cm}y_{\rm 2}^{\rm 2}\cdot f_{\it y_{\rm 2}}(\it y_{\rm 2})\hspace{0.1cm}{\rm d}y_{\rm 2}=\rm \frac{1}{2}\cdot\frac{1}{3}\cdot 1\,V^2+\rm \frac{1}{4}\cdot 1\,V^2 = 5/12 \,V^2 \hspace{0.15cm}{ =\rm 0.417\,V^2}.$$

Der erste Anteil geht auf die kontinuierliche WDF zurück, der zweite auf die WDF–Diracfunktion bei 1 V. Die Diracfunktion bei <nobr>0 V</nobr> liefert keinen Beitrag zur Leistung. Daraus folgt für den Effektivwert:

$$\sigma_{y_{\rm 2}} = \sqrt{{\rm 5}/{\rm 12}\rm V^2 -{1}/{4}\rm V^2}= \sqrt{{\rm 1}/{\rm 6}\rm V^2} \hspace{0.15cm}\underline{=0.409\, \rm V}.$$

9.  Diese Wahrscheinlichkeit setzt sich ebenfalls aus zwei Anteilen zusammen:

$${\rm Pr}(y_2 > 0.75 {\rm V} ) = {\rm Pr}(0.75 {\rm V} \le y_2 < 1 {\rm V} ) + {\rm Pr}(y_2 = 1 {\rm V} ) = \frac{1}{2} \cdot \frac{1}{4}+ \frac{1}{4} = \frac{3}{8}\hspace{0.15cm}\underline{ = 0.375}. $$