Aufgabe 3.9: Kennlinie für Cosinus-WDF

• Zurück zum Buch

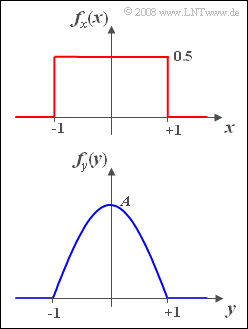
Gesucht ist eine stetige, monoton steigende nichtlineare Kennlinie y = g(x), die aus einer zwischen –1 und +1 gleichverteilten Zufallsgröße x eine neue Zufallsgröße y mit cosinusförmiger WDF generiert:

$$f_y(y)=A\cdot\rm cos(\frac{\rm \pi}{\rm 2}\cdot \it y).$$

Die Zufallsgröße y kann ebenfalls nur Werte zwischen −1 und +1 annehmen. Die beiden Dichtefunktionen f_x(x) und f_y(y) sind nebenstehend skizziert.

Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 3.6.

Fragebogen

1

Welche der nachfolgenden Aussagen sind zutreffend?

	Außerhalb des Bereichs -1 ≤ x ≤ +1 kann g(x) beliebig sein.
	Die Kennlinie muss symmetrisch um x = 0 sein: g(–x) = g(x).
	Die Zufallsgröße y hat eine kleinere Varianz als x.

2

Berechnen Sie den f_y(y)–Wert bei y = 0: A = f_y(0).

$A$ =

3

Bestimmen Sie die Steigung h'(y) der Umkehrfunktion x = h(y), wobei im Bereich |y| ≤ 1 stets h'(y) > 0 gelten soll? Welche Steigung gilt bei y = 0?

$h´(y=0)$ =

4

Berechnen Sie mit dem Ergebnis aus 3. den Funktionsverlauf x = h(y) unter der Nebenbedingung h(0) = 0. Welcher Wert ergibt sich für y = 1?

$h(y=1)$ =

5

Ermitteln Sie den Funktionsverlauf y = g(x) der gesuchten Kennlinie. Welcher Funktionswert ergibt sich an der Stelle x = 1?

$g(x = 1)$ =

Musterlösung

Musterlösung

1.  Richtig sind die Aussagen 1 und 3: Da x nur Werte zwischen ±1 annehmen kann, ist der Verlauf der Kennlinie außerhalb dieses Bereichs für die Zufallsgröße y ohne Belang.

Die Bedingung g(–x) = g(x) muss nicht eingehalten werden. Es gibt beliebig viele Kennlinien, die die gewünschte WDF erzeugen können. Allerdings ist die unter Punkt e) berechnete Kennlinie punktsymmetrisch: g(–x) = –g(x).

Schon die grafischen Darstellungen der beiden Dichtefunktionen zeigen, dass σ_y kleiner als σ_x ist.

2.  Das Integral über die WDF muss stets gleich 1 sein. Daraus folgt:

$$\int_{-\rm 1}^{\rm 1}A\cdot \rm cos(\frac{\pi}{\rm 2}\cdot\it y)\, {\rm d} y=\frac{A\cdot \rm 4}{\pi}\hspace{0.3cm} \Rightarrow\hspace{0.3cm} A=\frac{\pi}{\rm 4} \hspace{0.15cm}\underline{= \rm 0.785}.$$

3.  Die Transformationsformel kann wie folgt umgeformt werden:

$$f_y(y)=\frac{f_x(x)}{| g'(x)|}\Big|_{\, x=h(y)}=f_x(x)\cdot |h'(y)| \Big|_{\, x=h(y)}.$$

Die Umkehrfunktion h(y) einer monoton ansteigenden Kennlinie steigt ebenfalls monoton an. Deshalb kann auf die Betragsbildung verzichtet werden und man erhält:

$$h'(y)=\frac{f_y(y)}{f_x(x)\Big|_{\, x=h(y)}}={\pi}/{\rm 2}\cdot \rm cos({\pi}/{2}\cdot \it y).$$

An der Stelle y = 0 hat die Steigung den Wert π/2 ≈ 1.571.

4.  Man erhält durch (unbestimmte) Integration:

$$h(y)=\int h'(y)\, {\rm d} y + \it C = \frac{\rm \pi}{\rm 2}\cdot \frac{\rm 2}{\pi}\cdot \rm sin(\frac{\pi}{\rm 2}\cdot\it y) + \rm \it C.$$

Die Nebenbedingung h(y = 0) = 0 führt zur Konstanten C = 0 und damit zum Ergebnis:

$$h(y) = \rm sin({\pi}/{\rm 2}\cdot \it y) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} h(y = \rm 1) \hspace{0.15cm}\underline{= \rm 1}.$$

5.  Die Umkehrfunktion der in (d) ermittelten Funktion x = h(y) lautet:

$$y=g(x)={\rm 2}/{\rm \pi}\cdot \rm arcsin({\it x}).$$

Diese Kennlinie steigt im Bereich –1 ≤ x ≤ 1 von y = –1 bis y = +1 monoton an. Der gesuchte Wert ist also g(x = +1) = +1.