Aufgabe 4.7Z: Erzeugung einer 2D–WDF

• Zurück zum Buch

Ausgehend von statistisch unabhängigen Größen u und υ, die beide zwischen –1 und +1 gleichverteilt sind und somit jeweils die Varianz σ² = 2/3 besitzen, soll eine 2D-Zufallsgröße (x, y) generiert werden, wobei für die Komponenten gilt:

$$x = A \cdot u + B \cdot v + C,$$

$$y= D \cdot u + E \cdot v + F.$$

Die zu erzeugende 2D–Zufallsgröße (x, y) soll die folgenden statistischen Eigenschaften aufweisen:

• Die Varianzen seien σ_x² = 4 und σ_y² = 10.

• Die Zufallsgröße x sei mittelwertfrei.

• Für den Mittelwert von y gelte m_y = 1.

• Der Korrelationskoeffizient zwischen x und y betrage

$$\rho_{xy} = \sqrt{0.9} = 0.949.$$

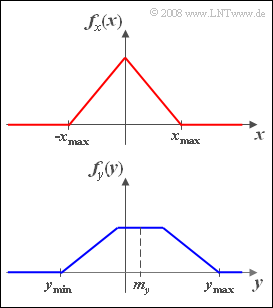
• Die Zufallsgröße x besitze eine dreieckförmige WDF f_x(x) entsprechend der oberen Grafik.

• Die Zufallsgröße y besitze eine trapezförmige WDF f_y(y) entsprechend der unteren Grafik.

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 4.3. Um Mehrdeutigkeiten zu vermeiden wird festgelegt, dass alle Koeffizienten A ... F nicht negativ sein sollen.

Fragebogen

1

Bestimmen Sie die Koeffizienten C und F.

$C$ =

$F$ =

2

Bestimmen Sie die Koeffizienten A und B.

$A$ =

$B$ =

3

Bestimmen Sie die Koeffizienten D und E, wobei D > E gelten soll.

$D$ =

$E$ =

4

Geben Sie die Maximalwerte für x und y an.

$x_\text{max}$ =

$y_\text{max}$ =

Musterlösung

Musterlösung

1.  Aufgrund der angegebenen Mittelwerte muss gelten: C = m_x = 0 und F = m_y = 1.

2.  Unter Berücksichtigung von σ² = 2/3 gilt:

$$\sigma_x^2 = \sigma^2 \cdot ( A^2 + B^2)= \frac {2}{3} \cdot ( A^2 + B^2) .$$

Wegen σ_x² = 4 folgt daraus A² + B² = 6. Eine dreieckförmige WDF bedeutet, dass A = ±B gelten muss. Somit erhält man A = B = 3^1/2 = 1.732 (negative Koeffizienten wurden ausgeschlossen).

3.  Mit A und B entsprechend Punkt b) verbleiben zwei Bestimmungsgleichungen für D und E:

$$\sigma_y^2 = \sigma^2 \cdot ( D^2 + E^2)= 10 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} D^2 + E^2 = \frac {\sigma_y^2}{\sigma^2} = \frac {10}{2/3} \stackrel{!}{=}15,$$

$$\rho_{xy} = \frac{A \cdot D + B \cdot E}{\sqrt{(A^2 + B^2)(D^2 + E^2)}} = \frac{\sqrt{3} \cdot (D + E)}{\sqrt{6 \cdot (D^2 + E^2)}} \stackrel{!}{=} \sqrt{0.9}.$$

Daraus folgt weiter:

$$D + E = \sqrt{1.8 \cdot ( D^2 + E^2)} = \sqrt{27} = 3 \sqrt{3}.$$

Die Gleichung führt in Verbindung mit D² + E² = 15 und der oben angegebenen Nebenbedingung (D > E) zum Ergebnis:

$$ D= 2 \sqrt{3}\hspace{0.15cm}\underline{ = 3.464}, \hspace{0.5cm}E= \sqrt{3} \hspace{0.15cm}\underline{= 1.732}.$$

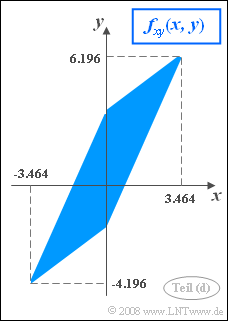
4.  Mit A = B = 1.732 kann die Zufallsgröße x maximal den Wert 3.464 annehmen (wenn jeweils u = 1 und υ = 1 gilt).

Das Maximum von y ergibt sich mit diesen Parameterwerten zu y_max = D + E + F = 6.196, der Minimalwert zu y_min = –D –E +F = –4.196 (siehe Skizze der 2D-WDF).