Aufgabe 2.2: Verzerrungsleistung

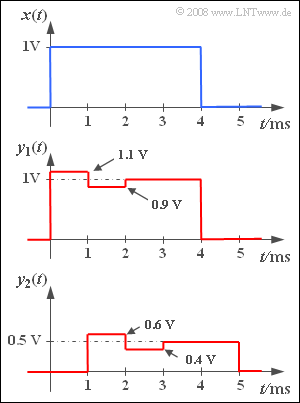
Am Eingang eines Nachrichtensystems S₁ wird ein Rechteckimpuls x(t) mit der Amplitude 1 V und der Dauer 4 ms angelegt. Am Systemausgang wird dann der Impuls y₁(t) gemessen, dessen Signalparameter der mittleren Skizze entnommen werden können.

Am Ausgang eines anderen Systems S₂ stellt sich bei gleichem Eingangssignal x(t) das in dem unteren Bild dargestellte Signal y₂(t) ein.

Für das in dieser Aufgabe verwendete Fehlersignal gelte folgende Definition:

$$\varepsilon(t) = y(t) - \alpha \cdot x(t - \tau) .$$

Die Parameter α und τ sind so zu bestimmen, dass die Verzerrungsleistung (der mittlere quadratische Fehler)

$$P_{\rm V} = \overline{\varepsilon^2(t)} = \frac{1}{T_{\rm M}} \cdot \int\limits_{ ( T_{\rm M})} {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t$$

minimal ist. Bei diesen Definitionen ist bereits berücksichtigt, dass eine frequenzunabhängige Dämpfung ebenso wie eine für alle Frequenzen konstante Laufzeit nicht zur Verzerrung beiträgt.

Das Integrationsintervall ist jeweils geeignet zu wählen. Benutzen Sie für y₁(t) den Bereich von 0 ... 4 ms und für y₂(t) das Intervall 1 ms ... 5 ms. T_M ist in beiden Fällen gleich 4 ms. Es ist offensichtlich, dass bezüglich y₁(t) die Parameter α = 1 und τ = 0 jeweils zur minimalen Verzerrungsleistung führen.

Das so genannte Signal–zu–Verzerrungs–Leistungsverhältnis berechnet sich im allgemeinen Fall zu

$$\rho_{\rm V} = \frac{ \alpha^2 \cdot P_{x}}{P_{\rm V}} \hspace{0.05cm}.$$

Hierbei gibt P_x die Leistung des Signals x(t) an und α² · P_x die Leistung von y(t) = α · x(t – τ), die sich bei Abwesenheit von Verzerrungen ergeben würde. Meist – so auch in dieser Aufgabe – wird dieses S/N-Verhältnis ρ_V logarithmisch in dB angegeben.

Fragebogen

$P_\text{V1}$ =

$V^2$

$10 \cdot lg \ \rho_\text{V1}$ =

$dB$

$\alpha$ =

$\tau$ =

$ms$

$P_\text{V2}$ =

$V^2$

$10 \cdot lg \ \rho_\text{V2}$ =

$dB$

Musterlösung

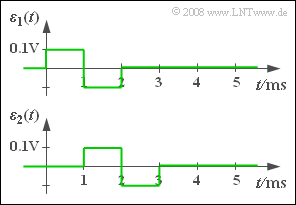
1. Mit den gegebenen Parametern α = 1 und τ = 0 erhält man das in der Grafik dargestellte Fehlersignal ε₁(t). Die Verzerrungsleistung ist somit gleich:

$$P_{\rm V1} = \frac{ {1 \, \rm ms}}{4 \, \rm ms} \cdot \left[ ({0.1 \, \rm V})^2 + ({-0.1 \, \rm V})^2\right] $$

$$\hspace{0.3cm}\Rightarrow P_{\rm V1} \hspace{0.15cm}\underline{ = {0.005 \, \rm V^2}}.$$

2. Die Leistung des Eingangssignals beträgt:

$$P_{x} = \frac{1}{4 \, \rm ms} \cdot ({1 \, \rm V})^2 \cdot {4 \, \rm ms}\hspace{0.15cm}{ = {1 \, \rm V^2}}.$$

Mit dem Ergebnis aus 1) erhält man somit für das Signal–zu–Verzerrungs–Leistungsverhältnis:

$$\rho_{\rm V1} = \frac{ P_{x}}{P_{\rm V1}}= \frac{ {1 \, \rm V^2}}{0.005 \, \rm V^2}\hspace{0.05cm}\rm = 200\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V1}\hspace{0.15cm}\underline{ = {23.01 \, \rm dB}}.$$

3. Die Skizze auf dem Angabenblatt macht deutlich, dass sich auch ohne die auftretenden Verzerrungen, sondern allein durch Dämpfung und Laufzeit, das Signal y(t) von x(t) deutlich unterscheiden würde. Es würde sich y(t) = 0.5 · x(t – 1 ms) ergeben.

Wenn jemand diese Parameterwerte nicht sofort aus der Grafik erkennt, so müsste er für sehr (unendlich) viele α– und τ–Werte zunächst das Fehlersignal

$$\varepsilon_2(t) = y_2(t) - \alpha \cdot x(t - \tau)$$

und anschließend den mitteleren quadratischen Fehler ermitteln, wobei das Integrationsintervall jeweils an τ anzupassen ist. Auch dann würde man das kleinstmögliche Ergebnis für α = 0.5 und τ = 1 ms erhalten. Für diese Optimierung von α und τ sollte man sich allerdings schon ein Computerprogramm gönnen.

4. Die obige Skizze zeigt, dass ε₂(t) bis auf eine Verschiebung um 1 ms gleich dem Fehlersignal ε₁(t) ist. Mit dem Integrationsintervall 1 ms ... 5 ms ergibt sich somit auch die gleiche Verzerrungsleistung:

$$P_{\rm V2} = P_{\rm V1} \hspace{0.15cm}\underline{= {0.005 \, \rm V^2}}.$$

5. Entsprechend dem Angabenblatt gilt:

$$\rho_{\rm V2} = \frac{ \alpha^2 \cdot P_{x}}{P_{\rm V2}}= \frac{ 0.5^2 \cdot {1 \, \rm V^2}}{0.005 \, \rm V^2}\hspace{0.05cm}\rm = 50\hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm V2} \hspace{0.15cm}\underline{= {16.99 \, \rm dB}}.$$

Trotz gleicher Verzerrungsleistung ist 10 · lg ρ_V2 gegenüber 10 · lg ρ_V1 um etwa 6 dB geringer. Das Signal y₂(t) ist also hinsichtlich des SNR deutlich ungünstiger als y₁(t). Hierbei ist berücksichtigt, dass nun wegen α = 0.5 die Leistung des Ausgangssignals nur noch ein Viertel der Eingangsleistung beträgt.

Würde man diese Dämpfung am Ausgang durch eine Verstärkung um 1/α kompensieren, so würde zwar die Verzerrungsleistung um α² größer. Das Signal-zu-Verzerrungs-Leistungsverhältnis ρ_V2 bliebe jedoch erhalten, weil auch das „Nutzsignal” um den gleichen Betrag angehoben wird.