Aufgabe 3.7: Hochpass-Impulsantwort
Aus LNTwww
Version vom 1. Oktober 2016, 01:01 Uhr von Nabil (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Laplace–Rücktransformation }} right| :Wir gehen von der nebensteh…“)
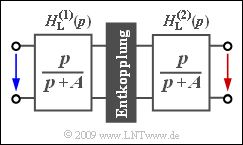
- Wir gehen von der nebenstehend skizzierten Anordnung aus. Die Übertragungsfunktionen der beiden Hochpässe lauten:
- $$H_{\rm L}^{(1)}(p) = H_{\rm L}^{(2)}(p) =\frac{p}{p+A} \hspace{0.05cm} .$$
- Da die Vierpole durch einen Trennverstärker widerstandsmäßig entkoppelt sind, lässt sich für die Gesamtübertragungsfunktion schreiben:
- $$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) \hspace{0.05cm} .$$
- Gleichzeitig ist bekannt, dass folgende Gleichung gültig ist:
- $$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4} \hspace{0.05cm} .$$
- Stellt man diese Funktion in Pol–Nullstellen–Form dar, so wird sich herausstellen, dass hier die Anzahl der Nullstellen (Z) gleich der Anzahl der Pole (N) ist. Eine direkte Anwendung des Residuensatzes ist hier deshalb nicht möglich.
- Um die Zeitfunktion h(t) berechnen zu können, muss eine Partialbruchzerlegung entsprechend
- $$H_{\rm L}(p) =1- H_{\rm L}\hspace{-0.05cm}'(p) \hspace{0.05cm}$$
- vorgenommen werden. Damit gilt für die Impulsantwort:
- $$h(t) = \delta(t)- h\hspace{0.03cm}'(t) \hspace{0.05cm}.$$
- Bezüglich HL'(p) gilt Z' < N'. Somit kann der kontinuierliche Anteil h'(t) der Impulsantwort wieder mit dem Residuensatz ermittelt werden.
- Hinweis: Die Aufgabe gehört zum Kapitel 3.3. Das Residium eines l–fachen Pols px innerhalb der Funktion HL(p) lautet:
- $${\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.7cm}\{H_{\rm L}(p)\cdot {\rm e}^{\hspace{0.05cm}p t}\}= \frac{1}{(l-1)!}\cdot \frac{{\rm d}^{\hspace{0.05cm}l-1}}{{\rm d}p^{\hspace{0.05cm}l-1}}\hspace{0.15cm} \left \{H_{\rm L}(p)\cdot (p - p_{\rm x})^{\hspace{0.05cm}l} \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.05cm} .$$
- Die Ableitung des Produkts y(x) = f(x) · g(x) ist wie folgt gegeben:
- $$\frac{{\rm d}{\hspace{0.05cm}y(x)}}{{\rm d}\hspace{0.05cm}x}= \frac{{\rm d}{\hspace{0.05cm}f(x)}}{{\rm d}\hspace{0.05cm}x}\cdot g(x) + \frac{{\rm d}{\hspace{0.05cm}g(x)}}{{\rm d}\hspace{0.05cm}x}\cdot f(x) \hspace{0.05cm} .$$
Fragebogen
Musterlösung
- 1. Ausgehend von der vorgegebenen Gleichung kann HL(p) wie folgt umgeformt werden:
- $$H_{\rm L}(p) =\frac{4}{1/p^2 + 4/p +4}=\frac{p^2}{p^2 + p +1/4}=\frac{p^2}{(p +1/2)^2} \hspace{0.05cm} $$
- $$\Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{ Z = 2\hspace{0.05cm} , \hspace{0.2cm}N = 2\hspace{0.05cm} , \hspace{0.2cm}K = 1} \hspace{0.05cm} .$$
- 2. Die Gesamtübertragungsfunktion lautet entsprechend der Angabe:
- $$H_{\rm L}(p) = H_{\rm L}^{(1)}(p) \cdot H_{\rm L}^{(2)}(p) =\frac{p^2}{(p+A)^2} \hspace{0.05cm} .$$
- Ein Vergleich mit dem Ergebnis der Teilaufgabe 1) zeigt, dass A = 0.5 sein muss.
- 3. Ausgehend von der unter a) berechneten Gleichung erhält man
- $$H_{\rm L}(p) =\frac{p^2}{p^2 + p +0.25}= \frac{p^2 + p +0.25}{p^2 + p +0.25}- \frac{p +0.25}{p^2 + p +0.25}$$
- $$ \Rightarrow \hspace{0.3cm}H_{\rm L}\hspace{-0.05cm}'(p) = \frac{p +0.25}{p^2 + p +0.25}= \frac{p +0.25}{(p +0.5)^2} \hspace{0.05cm} .$$
- Richtig ist dementsprechend der letzte Lösungsvorschlag.
- 4. Bezüglich der Funktion HL'(p) gilt Z' = 1, N' = 2 und K' = 1. Die beiden Pole bei px = –0.5 fallen zusammen, so dass nur ein Residium ermittelt werden muss:
- $$h\hspace{0.03cm}'(t) \hspace{0.25cm} = \hspace{0.2cm} {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{\rm x}} \hspace{0.7cm}\{H_{\rm L}\hspace{-0.05cm}'(p)\cdot {\rm e}^{p t}\}= \frac{\rm d}{{\rm d}p}\hspace{0.15cm} \left \{ \frac{p +0.25}{(p +0.5)^2} \cdot (p +0.5)^2 \cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5}=\\ = \hspace{0.2cm}\frac{\rm d}{{\rm d}p}\hspace{0.15cm} \left \{ (p +0.25) \cdot {\rm e}^{p \hspace{0.05cm}t}\right\} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} \hspace{0.05cm} .$$
- Mit der Produktregel der Differentialrechnung erhält man:
- $$h\hspace{0.03cm}'(t) \hspace{0.15cm} = \hspace{0.15cm} {\rm e}^{p \hspace{0.05cm}t} + ( p + 0.25) \cdot t \cdot {\rm e}^{\hspace{0.05cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}-0.5} =\\ = \hspace{0.15cm} (1- {t}/{4}) \cdot{\rm e}^{-t/2} \hspace{0.05cm} $$
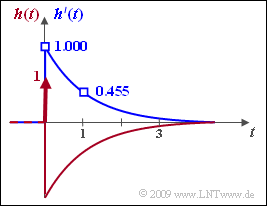
- $$\Rightarrow \hspace{0.3cm}h\hspace{0.03cm}'(t = 0) \hspace{0.15cm} = \underline{1}\hspace{0.05cm} ,\\ h\hspace{0.03cm}'(t = 1) \hspace{0.15cm} = \underline {0.455}\hspace{0.05cm} \\ h\hspace{0.03cm}'(t \rightarrow \infty) \hspace{0.15cm} = \underline {= 0}\hspace{0.05cm} .$$
- Die Grafik zeigt als blaue Kurve h'(t) und als rote Kurve die gesamte Impulsantwort
- $$h(t) = \delta (t) - (1- {t}/{4}) \cdot{\rm e}^{-t/2} \hspace{0.05cm}.$$