Aufgabe 4.8: Nebensprechstörungen

Auf dem S₀–Bus bei ISDN werden die Daten getrennt nach Übertragungsrichtung auf einem Sternvierer übertragen. Das Empfangssignal eines ISDN–Geräts wird daher außer von Verbindungen auf anderen Adern auch durch Nebensprechen von seinem eigenen Sendesignal gestört.

In dieser Aufgabe werden zwei ISDN–Terminals im Abstand von 50 m berechnet, wobei vorausgesetzt wird:

Für das Leistungsdichtespektrum (LDS) des Senders eines jeden Terminals gelte sehr stark vereinfacht mit Φ₀ = 5 · 10^-9 W/Hz:

$${\it\Phi}_{s}(f)= \left\{ \begin{array}{c} {\it\Phi}_{0} \\ 0 \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c} { |f| \le f_0 = 100\,{\rm kHz} \hspace{0.05cm},} \\ { |f| > f_0\hspace{0.05cm}.} \end{array}$$

Die Leistungsübertragungsfunktion auf dem S₀–Bus (0.6 mm Kupfer–Zweidrahtleitung, 50 Meter) soll im betrachteten Bereich 0 < |f| < 100 kHz wie folgt angenähert werden (stark vereinfacht):

$$|H_{\rm K}(f)|^2 = 0.9 - 0.04 \cdot \frac{|f|}[[:Vorlage:\rm MHz]]\hspace{0.05cm}.$$

Die Nahnebensprech–Leistungsübertragungsfunktion ist wie folgt gegeben (NEXT steht dabei für Near–End–Crosstalk):

$$|H_{\rm NEXT}(f)|^2 = \left ( K_{\rm NEXT} \cdot |f|\right )^{3/2}\hspace{0.05cm},\hspace{0.2cm}K_{\rm NEXT} = 6 \cdot 10^{-10}\,{\rm s} \hspace{0.05cm}.$$

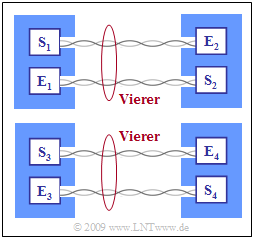
Die Grafik zeigt die betrachtete Systemkonfiguration. Mit zwei Doppeladern sind die Teilnehmer 1 und 2 verbunden (je eine in beide Richtungen), während auf zwei anderen Doppeladern (nicht im gleichen Sternvierer) eine Verbindung zwischen Teilnehmer 3 und Teilnehmer 4 besteht.

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.3 in diesem Buch sowie auf das Kapitel 1.2 im Buch „Beispiele von Nachrichtensystemen”.

Fragebogen

	Der Sender S₁ führt bei Empfänger E₂ zu Nahnebensprechen.
	Der Sender S₂ führt bei Empfänger E₂ zu Nahnebensprechen.
	Der Sender S₃ führt bei Empfänger E₂ zu Nahnebensprechen.
	Nahnebensprechen ist unangenehmer als Fernnebensprechen.

$P_S$ =

$\cdot 10^{-3}\ W$

$P_E$ =

$\cdot 10^{-3}\ W$

$P_\text{NEXT}$ =

$\cdot 10^{-9}\ W$

$10 \cdot \ lg\ P_E/P_\text{NEXT}$ =

$dB$

Musterlösung

1. Nebensprechen entsteht durch Kopplungen der übertragenen Signale auf benachbarte Doppeladern. Bei Nahnebensprechen (NEXT) befinden sich der störende Sender und der gestörte Empfänger am selben Ende der Leitung, bei Fernnebensprechen (FEXT) an unterschiedlichen Enden. Da aber auch die Störsignale auf der Kupferdoppelader sehr stark gedämpft werden, ist NEXT gegenüber FEXT stets der bei Weitem dominante Störeffekt.

Richtig sind hier die Lösungsvorschläge 2 und 4. Der Empfänger E₂ wird hier besonders durch seinen eigenen Sender S₂, also durch Nahnebensprechen gestört. Die Beeinträchtigung von E₂ durch S₃ ist Fernnebensprechen, während S₁ für E₂ das Nutzsignal bereitstellt.

2. Die Sendeleistung ist gleich dem Integral über das Leistungsdichtespektrum:

$$P_{\rm S} = {\it\Phi}_{0} \cdot 2 f_0 = 5 \cdot 10^{-9}\, {\rm W}/{\rm Hz} \cdot 2 \cdot 10^{5}\,{\rm Hz}\hspace{0.15cm}\underline{ = 10^{-3}\,{\rm W}} \hspace{0.05cm}.$$

3. Für die Empfangsleistung gilt (ohne den Anteil durch Nahnebensprechen):

$$P_{\rm E} = \int\limits_{-\infty}^{ +\infty} {\it\Phi}_{s}(f) \cdot |H_{\rm K}(f)|^2 \hspace{0.1cm}{\rm d}f = 2 {\it\Phi}_{0} \cdot \int\limits_{0}^{ f_0} \left [ 0.9 - 0.04 \cdot \frac{f}{f_0} \right ] \hspace{0.1cm}{\rm d}f = \\ = 2 {\it\Phi}_{0} \cdot \left [ 0.9 \cdot f_0 - \frac{0.04}{2} \cdot \frac{f_0^2}{f_0} \right ] = 2 {\it\Phi}_{0} \cdot 0.88 = 0.88 \cdot P_{\rm S}\hspace{0.15cm}\underline{ = 0.88 \cdot 10^{-3}\,{\rm W}} \hspace{0.05cm}.$$

4. Für diesen störenden Leistungsanteil erhält man

$$P_{\rm NEXT} = \int\limits_{-\infty}^{ +\infty} {\it\Phi}_{s}(f) \cdot |H_{\rm NEXT}(f)|^2 \hspace{0.1cm}{\rm d}f = 2 {\it\Phi}_{0} \cdot K_{\rm NEXT}^{3/2} \cdot \int\limits_{0}^{ f_0} f^{3/2} \hspace{0.1cm}{\rm d}f = \\ = \frac{4}{5} \cdot {\it\Phi}_{0} \cdot K_{\rm NEXT}^{3/2} \cdot f_0^{5/2} = 0.8 \cdot 5 \cdot 10^{-9}\, \frac{\rm W}{\rm Hz} \cdot \left ( 6 \cdot 10^{-10}\,{\rm s}\right )^{3/2} \cdot \left ( 10^{5}\,{\rm Hz}\right )^{5/2} = \\\\ = \hspace{0.15cm}\underline{0.186 \cdot 10^{-9}\,{\rm W}} \hspace{0.05cm}.$$

5. Das Verhältnis P_E/P_NEXT ist ca. 4.73 · 10⁶. Daraus ergibt sich der logarithmische Wert zu

$$10 \cdot {\rm lg}\hspace{0.15cm} \frac{P_{\rm E}}{P_{\rm NEXT}} = 10 \cdot {\rm lg}\hspace{0.15cm} 4.73 \cdot 10^{6} \hspace{0.15cm}\underline{= 66.7\,\,{\rm dB}} \hspace{0.05cm}.$$