Aufgabe 2.8: Huffman-Anwendung bei einer Markovquelle

• Zurück zum Buch

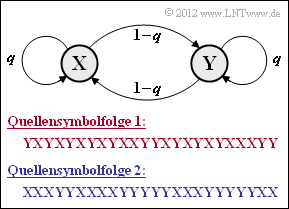
Wir betrachten hier die binäre symmetrische Markovquelle entsprechend nebenstehender Grafik, die durch den einzigen Parameter

$$q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y})$$

vollständig beschrieben wird. Die angegebenen Quellensymbolfolgen gelten für q = 0.2 bzw. q = 0.8. In der Teilaufgabe (a) ist zu klären, welche Symbolfolge mit q = 0.2 und welche mit q = 0.8 generiert wurde.

Die Eigenschaften von Markovquellen werden im Kapitel 1.2 ausführlich beschrieben. Aufgrund der hier vorausgesetzten Symmetrie bezüglich der binären Symbole X und Y ergeben sich einige gravierende Vereinfachungen, wie in Aufgabe Z1.5 hergeleitet wird:

• Die Symbole X und Y sind gleichwahrscheinlich, das heißt. es ist p_X = p_Y = 0.5. Damit lautet die erste Entropienäherung:

$$H_1 = 1\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}. $$

• Die Entropie der Markovquelle ergibt sich zu

$$H = q \cdot {\rm ld}\hspace{0.15cm}\frac{1}{q} + (1-q) \cdot {\rm ld}\hspace{0.15cm}\frac{1}{1-q} = 0.722\,\,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$

Der Zahlenwert gilt nur für q = 0.2 sowie für q = 0.8.

• Bei Markovquellen sind alle Entropienäherungen höherer Ordnung durch H₁ und H bestimmt. Die folgenden Zahlenwerte gelten wieder für q = 0.2 und q = 0.8 gleichermaßen:

$$H_2 \hspace{0.2cm} = \hspace{0.2cm} \frac{1}{2}\cdot \big [ H_1 + H \big ] = 0.861\,\,{\rm bit/Quellensymbol}\hspace{0.05cm},\\ H_3 \hspace{0.2cm} = \hspace{0.2cm} \frac{1}{3} \cdot \big [ H_1 + 2H \big ] = 0.815\,\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$

Wie auf der letzten Theorieseite dieses Kapitels 2.3 soll hier der Huffman–Algorithmus auf k–Tupel angewandt werden, wobei wir uns auf k = 2 und k = 3 beschränken.

Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 2.3. Nützliche Informationen finden Sie auch in Aufgabe A2.7 und Aufgabe Z2.7. Für die Huffman–Codierung können Sie das folgende Interaktionsmodul benutzen:

Shannon–Fano– und Huffman–Codierung

Fragebogen

1

Welche der vorne angegebenen Beispielfolgen gilt für q = 0.8?

	Quellensymbolfolge 1,
	Quellensymbolfolge 2,

2

Welche der folgenden Aussagen treffen zu?

	Auch die direkte Anwendung von Huffman ist hier sinnvoll.
	Huffman macht bei Bildung von Zweiertupeln (k = 2) Sinn.
	Huffman macht bei Bildung von Dreiertupeln (k = 3) Sinn.

3

Wie lauten die Wahrscheinlichkeiten der Zweiertupel (k = 2) für q = 0.8?

$q = 0.8; k = 2:\ p_A = Pr(XX)$ =

$p_B = Pr(XY)$ =

$p_C = Pr(YX)$ =

$p_D = Pr(YY)$ =

4

Ermitteln Sie mit dem angegebenen Flash–Modul den Huffman–Code für k = 2. Wie groß ist in diesem Fall die mittlere Codewortlänge?

$L_M$ = bit/Quellensymbol

5

Welche Schranke ergibt sich für die mittlere Codewortlänge, wenn Zweiertupel gebildet werden (k = 2)? Interpretation.

	LM ≥ H1 = 1 bit/Quellensymbol,
	LM ≥ H2 ≈ 0.861 bit/Quellensymbol,
	LM ≥ H3 ≈ 0.815 bit/Quellensymbol,
	LM ≥ H ≈ 0.722 bit/Quellensymbol,
	LM ≥ 0.5 bit/Quellensymbol.

6

Berechnen Sie die Wahrscheinlichkeiten für k = 3.

$q = 0.8; k = 3:\ p_A = Pr(XXX)$ =

$p_B = Pr(XXY)$ =

$p_C = Pr(XYX)$ =

$p_D = Pr(XYY)$ =

$p_E = Pr(YXX)$ =

$p_F = Pr(YXY)$ =

$p_G = Pr(YYX)$ =

$p_H = Pr(YYY)$ =

7

Ermitteln Sie mit dem genannten Flash–Modul den Huffman–Code für k = 3. Wie groß ist in diesem Fall die mittlere Codewortlänge?

$L_M$ = bit/Quellensymbol

Musterlösung

Musterlösung

1.  Bei der Quellensymbolfolge 2 erkennt man sehr viel weniger Symbolwechsel als in der roten Folge. Die blaue Symbolfolge 2 wurde mit dem Parameter

$$q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.8$$

erzeugt und die rote Symbolfolge 1 mit q = 0.2   ⇒   Richtig ist der Lösungsvorschlag 2.

2.  Da hier die Quellensymbole X und Y gleichwahrscheinlich angenommen wurden, macht die direkte Anwendung von Huffman keinen Sinn. Dagegen kann man die inneren statistischen Bindungen der Markovquelle zur Datenkomprimierung nutzen, wenn man k–Tupel bildet (k ≥ 2). Richtig sind demnach die Antworten 2 und 3. Je größer k ist, desto mehr nähert sich die Codewortlänge L_M der Entropie H.

3.  Die Symbolwahrscheinlichkeiten p_X und p_Y sind jeweils 0.5. Damit erhält man für die Zweiertupel:

$$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XX}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot q = 0.5 \cdot 0.8 \hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm},\\ p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XY}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},\\ p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YX}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},\\ p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YY}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot q = 0.5 \cdot 0.8\hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm}.$$

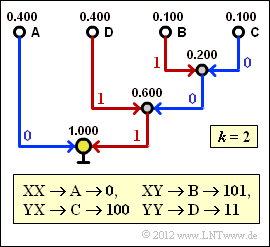
4.  Nebenstehender Bildschirmabzug des Programms Shannon–Fano– und Huffman–Codierung zeigt die Konstruktion des Huffman–Codes für k = 2 mit den soeben berechneten Wahrscheinlichkeiten. Damit gilt für die mittlere Codewortlänge:

$$L_{\rm M}' \hspace{0.2cm} = \hspace{0.2cm} 0.4 \cdot 1 + 0.4 \cdot 2 + (0.1 + 0.1) \cdot 3 = \\ \hspace{0.2cm} = 1.8\,\,{\rm bit/Zweiertupel}$$

$$\Rightarrow\hspace{0.3cm}L_{\rm M} = \frac{L_{\rm M}'}{2}\hspace{0.15cm}\underline{ = 0.9\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$

5.  Nach dem Quellencodierungstheorem gilt L_M ≥ H. Wendet man aber Huffman–Codierung an und lässt dabei Bindungen zwischen nicht benachbarten Symbolen außer Betracht (k = 2), so gilt als unterste Grenze der Codewortlänge nicht H = 0.722, sondern H₂ = 0.861 (auf den Zusatz bit/Quellensymbol wird für den Rest der Aufgabe verzichtet)  ⇒ Lösungsvorschlag 2.

Das Ergebnis der Teilaufgabe 4) war L_M = 0.9. Würde eine unsymmetrische Markovkette vorliegen und zwar derart, dass sich für die Wahrscheinlichkeiten p_A, ... , p_D die Werte 50%, 25% und zweimal 12.5% ergeben würden, so käme man auf die mittlere Codewortlänge L_M = 0.875. Wie die genauen Parameter dieser unsymmetrischen Markovquelle aussehen, weiß ich (G. Söder) nicht. Auch nicht, wie sich der Wert 0.875 auf 0.861 senken ließe. Der Huffman–Algorithmus ist hierfür jedenfalls ungeeignet.

6.  Mit q = 0.8 und 1 – q = 0.2 erhält man:

$$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXX}) = 0.5 \cdot q^2 \hspace{0.15cm}\underline{ = 0.32} = p_{\rm H} = {\rm Pr}(\boldsymbol{\rm YYY})\hspace{0.05cm},\\ p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXY}) = 0.5 \cdot q \cdot (1-q) \hspace{0.15cm}\underline{ = 0.08}= p_{\rm G} = {\rm Pr}(\boldsymbol{\rm YYX}) \hspace{0.05cm},\\ p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYX}) = 0.5 \cdot (1-q)^2\hspace{0.15cm}\underline{ = 0.02} = p_{\rm F}= {\rm Pr}(\boldsymbol{\rm YXY}) \hspace{0.05cm},\\ p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYY}) = 0.5 \cdot (1-q) \cdot q \hspace{0.15cm}\underline{ = 0.08} = p_{\rm E} = {\rm Pr}(\boldsymbol{\rm YXX})\hspace{0.05cm}.$$

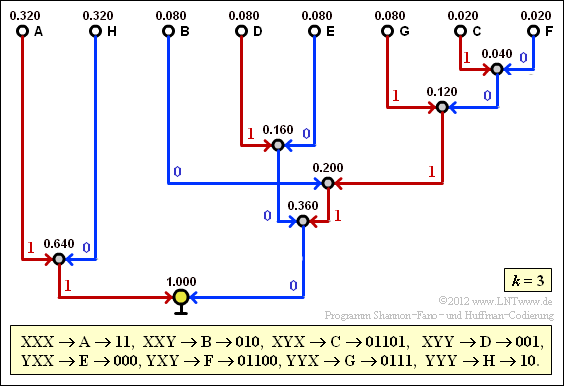
7.  Der Bildschirmabzug des Flash–Moduls verdeutlicht die Konstellation des Huffman–Codes für k = 3. Damit erhält man für die mittlere Codewortlänge:

$$L_{\rm M}' = 0.64 \cdot 2 + 0.24 \cdot 3 + 0.04 \cdot 5 = 2.52\,\,{\rm bit/Dreiertupel}$$

$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}'}/{3}\hspace{0.15cm}\underline{ = 0.84\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$

Man erkennt die Verbesserung gegenüber (4). Die für k = 2 gültige informationstheoretische Schranke H₂ = 0.861 wird nun unterschritten (L_M). Die neue Schranke für k = 3 ist H₃ = 0.815. Um die Quellenentropie H = 0.722 zu erreichen (besser gesagt: diesem Endwert bis auf ein ε näher zu kommen), müsste man allerdings unendlich lange Tupel bilden (k → ∞).