Aufgabe 2.7Z: Huffman-Codierung für Zweiertupel einer Ternärquelle

• Zurück zum Buch

Wir betrachten den gleichen Sachverhalt wie in der Aufgabe A2.7: Der Huffman–Algorithmus führt zu einem besseren Ergebnis, das heißt zu einer kleineren mittleren Codewortlänge L_M, wenn man ihn nicht auf einzelne Symbole anwendet, sondern vorher k–Tupel bildet. Dadurch erhöht man den Symbolumfang von M auf M ′ = M ^k.

Für die hier betrachtete Nachrichtenquelle gilt:

• Symbolumfang: M = 3,

• Symbolvorrat: {X, Y, Z},

• Wahrscheinlichkeiten: p_X = 0.7, p_Y = 0.2, p_Z = 0.1,

• Entropie: H = 1.157 bit/Ternärsymbol.

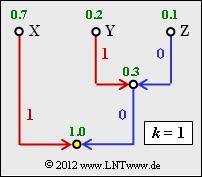
Die Grafik zeigt den Huffman–Baum, wenn man den Huffman–Algorithmus auf Einzelsymbole anwendet, also den Fall k = 1. In der Teilaufgabe (2) sollen Sie den entsprechenden Huffman–Code angeben, wenn vorher Zweiertupel gebildet werden (k = 2).

Hinweis: Die Aufgabe bezieht sich auf die letzte Theorieseite von Kapitel 2.3. Bezeichnen Sie die möglichen Zweiertupel mit

XX = A,  XY = B,  XZ = C,   YX = D,  YY = E,  YZ = F,  ZX = G,  ZY = H,  ZZ = I .

Fragebogen

1

Wie groß ist die mittlere Codewortlänge, wenn der Huffman–Algorithmus direkt auf die ternären Quellensymbole X, Y und Z angewendet wird?

$k = 1:\ L_M$ = bit/Quellensymbol

2

Wie groß sind die Tupel–Wahrscheinlichkeiten? Insbesondere:

$p_A = Pr(XX)$ =

$p_B = Pr(XY)$ =

$p_C = Pr(XZ)$ =

3

Wie groß ist die mittlere Codewortlänge, wenn man erst Zweiertupel bildet und darauf den Huffman–Algorithmus anwendet.

$k = 2:\ L_M$ = bit/Quellensymbol

4

Welche der folgenden Aussagen sind zutreffend, wenn man mehr als zwei Ternärzeichen zusammenfasst (k >2)?

	LM fällt monoton mit steigendem k ab.
	LM ändert sich nicht, wenn man k erhöht.
	Für k = 3 erhält man LM = 1.05 bit/Quellensymbol.

Musterlösung

Musterlösung

1.  Die mittlere Codewortlänge ergibt sich mit p_X = 0.7, L_X = 1, p_Y = 0.2, L_Y = 2, p_Z = 0.1, L_Z = 2 zu

$$L_{\rm M} = p_{\rm X} \cdot 1 + (p_{\rm Y} + p_{\rm Z}) \cdot 2 \hspace{0.15cm}\underline{= 1.3\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}. $$

Dieser Wert liegt noch deutlich über der Quellenentropie H = 1.157 bit/Quellensymbol.

2.  Es gibt M ′ = M ² = 3² = 9 Zweiertupel mit folgenden Wahrscheinlichkeiten:

p_A = Pr(XX) = 0.49,   p_B = Pr(XY) = 0.14,    p_C = Pr(XZ) = 0.07,

p_D = Pr(YX) = 0.14,    p_E = Pr(YY) = 0.04,    p_F = Pr(YZ) = 0.02,

p_G = Pr(YX) = 0.07,    p_H = Pr(YY) = 0.02,    p_I = Pr(YZ) = 0.01.

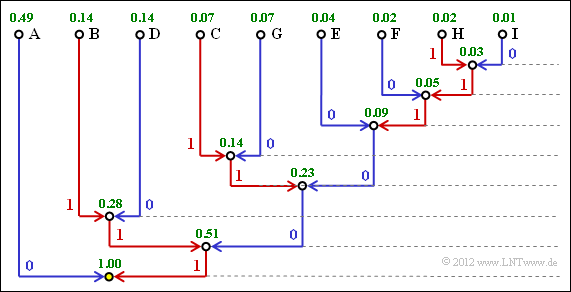
3.  Die Grafik zeigt den Huffman–Baum für die Anwendung mit k = 2.

Damit erhält man

• für die einzelnen Zweiertupels folgende Binärcodierungen:
  

XX = A → 0,   XY = B → 111,   XZ = C → 1011,    YX = D → 110,   YY = E → 1000,

YZ = F → 10010,    ZX = G → 1010,   ZY = H → 100111,   ZZ = I → 100110 .

• für die mittlere Codewortlänge:

$$L_{\rm M}' \hspace{0.2cm} = \hspace{0.2cm} 0.49 \cdot 1 + (0.14 + 0.14) \cdot 3 + (0.07 + 0.04 + 0.07) \cdot 4 + \\ \hspace{0.2cm} + \hspace{0.2cm}0.02 \cdot 5 + (0.02 + 0.01) \cdot 6 = 2.33\,\,{\rm bit/Zweiertupel}$$

$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}'}/{2}\hspace{0.15cm}\underline{ = 1.165\,\,{\rm bit/Quellensymbol}}\hspace{0.05cm}.$$

4.  Richtig ist Aussage 1, auch wenn L_M mit wachsendem k nur sehr langsam abfällt.

• Die letzte Aussage ist falsch, da L_M auch für k → ∞ nicht kleiner sein kann als H = 1.157 bit/Quellensymbol.

• Aber auch die zweite Aussage ist falsch: Da mit k = 2 weiterhin L_M > H gilt, führt k = 3 zu einer Verbesserung.