Aufgabe 4.1Z: Hochpass-System
Die auf Seite 3 dieses Abschnittes dargestellten Beziehungen gelten nicht nur für Signale und Spektren, sondern in gleicher Weise auch für Frequenzgang $H(f)$ und Impulsantwort $h(t)$ eines LZI-Systems; auch diese stehen über die Fouriertransformation im Zusammenhang. Nähere Informationen hierzu finden Sie im Buch „Lineare zeitinvariante Systeme”.
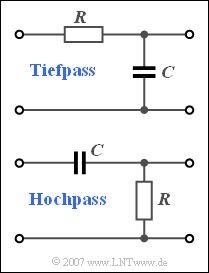
Die Schaltung gemäß dem oberen Bild ist die einfachste Realisierung eines Tiefpasses. Für sehr hohe Frequenzen wirkt die Kapazität $C$ als Kurzschluss, so dass hochfrequente Anteile im Ausgangssignal nicht mehr enthalten sind. Dagegen werden niederfrequente Signalanteile durch den Spannungsteiler nur unmerklich abgeschwächt.
Mit der 3dB-Grenzfrequenz $f_G$ gilt für den Frequenzgang:
- $$H_{\rm TP}(f) = \frac{1}{1 + {\rm j} \cdot f / f_{\rm G}} = |H_{\rm TP}(f)|\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_{\rm TP}(f)} .$$
Im zweiten Gleichungsteil ist der Frequenzgang $H_{TP}(f)$ nach Betrag und Phase aufgespalten.
Die Impulsantwort $h_{TP}(t)$ erhält man durch Fouriertransformation von $H_{TP}(f)$, wobei
- $$\tau = R \cdot C = \frac{1}{2\pi \cdot f_{\rm G}} $$
zu setzen ist. Für $t < 0$ ist die Impulsantwort identisch $0$, für positive Zeiten gilt:
- $$h_{\rm TP}(t) = \frac{1}{\tau} \cdot {\rm e}^{-t / \tau} .$$
Die unten dargestellte Schaltung beschreibt einen Hochpass, dessen Frequenzgang $H_{HP}(f)$ und Impulsantwort $h_{HP}(t)$ in dieser Aufgabe ermittelt werden sollen. Ein solcher Hochpass kann auch als Grenzfall eines Bandpasses interpretiert werden.
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 4.1.
Fragebogen
Musterlösung