Aufgabe 4.10Z: Korrelationsdauer
Aus LNTwww
Version vom 13. Oktober 2016, 20:25 Uhr von Nabil (Diskussion | Beiträge) (Nabil verschob die Seite Zusatzaufgaben:4.10 Korrelationsdauer nach 4.10Z Korrelationsdauer)
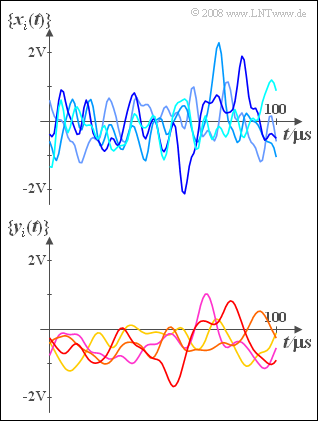
- Das nebenstehende Bild zeigt Mustersignale von zwei Zufallsprozessen mit jeweils gleicher Leistung Px = Py = 5 mW. Vorausgesetzt ist hierbei der Widerstand R = 50 Ω. Der Prozess {xi(t)}
- ist mittelwertfrei (mx = 0),
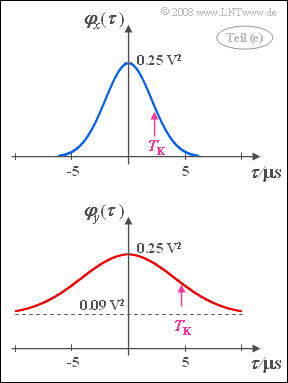
- besitzt die gaußförmige AKF
- $$\varphi_x (\tau) = \varphi_x (\tau = 0) \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2},$$
- und weist eine äquivalente AKF-Dauer ∇τx von 5 Mikrosekunden auf.
- Wie aus dem unteren Bild zu erkennen ist, weist der Prozess {yi(t)} sehr viel stärkere innere statistische Bindungen auf.
- Oder anders ausgedrückt: Der Zufallsprozess {yi(t)} ist niederfrequenter als {xi(t)}, und die äquivalente AKF-Dauer ist ∇τy = 10 μs.
- Aus der Skizze ist auch zu erkennen, dass {yi(t)} nicht gleichsignalfrei ist. Der Gleichsignalanteil beträgt vielmehr my = –0.3 V.
- Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.4.
Fragebogen
Musterlösung
- 1. Der quadratische Mittelwert ergibt sich zu R · Px = 50 Ω · 5 mW = 0.25 V2. Daraus folgt der Effektivwert σx = 0.5V.
- 2. Wegen Px = φx(τ = 0) gilt für die AKF allgemein:
- $$\varphi_x (\tau) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2}.$$
- Daraus erhält man:
- $$\varphi_x (\tau = {\rm 2\hspace{0.1cm} \mu s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- {\rm 0.16 }\pi } \hspace{0.15cm}\underline{= 3.025 \hspace{0.1cm} \rm mW},$$
- $$\varphi_x (\tau = {\rm 5\hspace{0.1cm} \rm \mu s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi } \hspace{0.15cm}\underline{= 0.216 \hspace{0.1cm} \rm mW}.$$
- 3. Hier gilt folgende Bestimmungsgleichung:
- $${\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(T_{\rm K} / {\rm \nabla} \tau_x)^2} \stackrel{!}{=} {\rm 0.5} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} (T_{\rm K} / {\rm \nabla} \tau_x)^2 = \sqrt{{ ln(2)}/{\pi}}\hspace{0.05cm}.$$
- Daraus folgt TK = 2.35 μs. Bei anderer AKF-Form erhält man ein anderes Verhältnis für TK/∇τx.
- 4. Wegen Px = Py sind die quadratischen Mittelwerte von x und y gleich, und zwar jeweils 0.25 V2. Unter Berücksichtigung des Mittelwertes my = –0.3 V gilt:
- $$m_y^2 + \sigma_y^2 = \rm 0.25 V^2.$$
- Daraus folgt σy = 0.4 V.
- 5. Bezogen auf den Einheitswiderstand R = 1 Ω lautet die AKF des Prozesses {yi(t)}:
- $$\varphi_y (\tau) = m_y^2 + \sigma_y^2 \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}.$$
- Rechts sehen Sie den Funktionsverlauf. Bezogen auf den Widerstand R = 50 Ω ergeben sich die nachfolgend angegebenen AKF-Werte:
- $$\varphi_y (\tau = 0) = 5 \hspace{0.1cm} {\rm mW} , \hspace{0.1cm} \atop \varphi_y (\tau \rightarrow \infty) = 1.8\hspace{0.1cm} {\rm mW} .$$
- Daraus folgt:
- $$\varphi_y(\tau) = 1.8 \hspace{0.1cm} {\rm mW} + 3.2 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}$$
- mit dem Zahlenwert 1.938 mW bei τ = 10 μs. Bei positivem Mittelwert my (mit gleichem Betrag) würde sich an der AKF nichts ändern, da my in die AKF-Gleichung quadratisch eingeht.