Aufgabe 5.2Z: Zweiwegekanal

• Zurück zum Buch

Von einem Übertragungssystem ist bekannt, dass zwischen dem Eingangssignal x(t) und dem Ausgangssignal y(t) der folgende Zusammenhang besteht:

$$y(t) = x( {t - \tau _1 } ) + \alpha \cdot x( {t - \tau _2 } ).$$

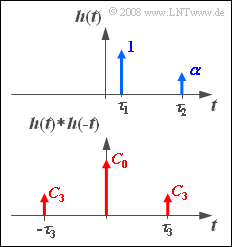
Die dazugehörige Impulsantwort h(t) ist rechts skizziert.

Verwenden Sie für die numerischen Berechnungen stets den Wert α = 0.5. Für die Teilaufgaben (1) und (2) gelte zudem τ₁ = 0 und τ₂ = 4 ms. Für die späteren Aufgabenteile soll von τ₁ = 1 ms und τ₂ = 5 ms ausgegangen werden.

In der unteren Skizze ist die Funktion

$$h(t) * h( { - t} )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\left| {H(f)} \right|^2$$

dargestellt, wobei die Parameter C₀, C₃ und τ₃ von α, τ₁ und τ₂ abhängen (siehe Teilaufgabe 4).

Das Eingangssignal x(t) sei bandbegrenztes weißes Rauschen mit der Leistungsdichte N₀ = 1 μW und der Bandbreite B = 10 kHz, woraus sich die Leistung P_x = 10 mW berechnen lässt.

Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.1.

Fragebogen

1

Berechnen Sie den Frequenzgang H(f) für τ₁ = 0 und τ₂ = 4 ms. Zeigen Sie, dass H(f) eine mit f₀ periodische Funktion ist. Wie groß ist f₀?

$f_0$ = $kHz$

2

Wie groß ist |H(f = 0)|² mit τ₁ = 0, τ₂ = 4 ms, α = 0.5?

$|H(f = 0)|^2$ =

3

Wie verändert sich die Funktion |H(f)|² mit τ₁ = 1 ms und τ₂ = 5 ms? Die Dämpfungskonstante α sei weiterhin 0.5. Geben Sie den Wert bei f = 0 ein.

$|H(f = 0)|^2$ =

4

Es gelte weiterhin α = 0.5, τ₁ = 1 ms und τ₂ = 5 ms. Welche Werte ergeben sich für die Funktionsparameter von h(t) ∗ h(–t) entsprechend der Skizze?

$C_0$ =

$C_3$ =

$\tau_3$ = $ms$

5

Wie groß ist die Leistung des Ausgangssignals y(t)?

$P_y$ = $mW$

Musterlösung

Musterlösung

1.  H(f) ist die Fouriertransformierte zu h(t). Mit dem Verschiebungssatz lautet diese (τ₁ = 0):

$$H(f) = 1 + \alpha \cdot {\rm{e}}^{ - {\rm{j2\pi }}f\tau _2 } = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$

Falls H(f) periodisch mit f₀ ist, muss für alle ganzzahligen Werte von i gelten:

$$H( {f + i \cdot f_0 } ) = H( f ).$$

Mit f₀ = 1/τ₂ = 0.25 kHz ist diese Bedingung erfüllt.

$$H( {f + i \cdot f_0 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) \\= 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$

2.  Das Betragsquadrat ist die Summe von quadriertem Realteil und quadriertem Imaginärteil:

$$\left| {H( f )} \right|^2 = \left( {1 + \alpha \cdot \cos ( A )} \right)^2 + \left( {\alpha \cdot \sin ( A )} \right)^2 .$$

Hierbei ist das Argument der Winkelfunktionen mit A = 2πfτ₂ abgekürzt. Nach Ausmultiplizieren unter Berücksichtigung von cos²(A) + sin²(A) = 1 erhält man:

$$\left| {H(f)} \right|^2 = 1 + \alpha ^2 + 2\alpha \cdot \cos ( A ).$$

Bei der Frequenz f = 0 (und somit A = 0) ergibt sich allgemein bzw. mit α = 0.5:

$$\left| {H( {f = 0} )} \right|^2 = \left( {1 + \alpha } \right)^2 = 1.5^2\hspace{0.15cm} \underline{ = 2.25}.$$

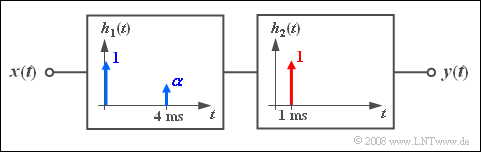
3.  Nun lässt sich das Übertragungssystem aus zwei Teilsystemen zusammensetzen (siehe Skizze):

Die Übertragungsfunktion H₁(f) ist wie unter b) berechnet. Für H₂(f) gilt mit τ₁ = 1 ms:

$$H_2 (f) = {\rm{e}}^{ - {\rm{j2\pi }}f\tau _1 } \quad \Rightarrow \quad \left| {H_2 (f)} \right| = 1\quad \Rightarrow \quad \left| {H_2 (f)} \right|^2 = 1.$$

Das bedeutet: Durch die zusätzliche Laufzeit wird |H(f)|² gegenüber der Teilaufgabe b) nicht verändert. Bei der Frequenz f = 0 gilt also weiterhin |H(f = 0)|² = 2.25.

4.  Durch Vergleich der gezeichneten Funktion h(t) ∗ h(–t) mit dem Ergebnis von b) erhält man:

$$C_0 = 1 + \alpha ^2 \hspace{0.15cm} \underline{= 1.25}, \hspace{0.5cm}C_3 = \alpha \hspace{0.15cm} \underline{= 0.5}, \hspace{0.5cm}\tau _3 = \tau _2 - \tau _1 \hspace{0.15cm} \underline{= 4\;{\rm{ms}}}.$$

5.  Das LDS des Ausgangssignals y(t) ist auf den Bereich von ±B begrenzt und ergibt sich zu

$${\it \Phi}_y(f) = {N_0}/{2} \cdot |H(f)|^2 = N_0/{2} \cdot {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}.$$

Unter Ausnutzung von Symmetrieeigenschaften erhält man somit für die Leistung:

$$P_y = N_0 \cdot \int_0^B {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}\hspace{0.1cm} {\rm{d}}f.$$

Da B = 10 kHz ein ganzzahliges Vielfaches der Frequenzperiode f₀ = 1/τ₃ = 250 Hz ist (vgl. Lösung zu Teilaufgabe 1), trägt die Cosinus-Funktion nicht zum Integral bei, und man erhält:

$$P_y = N_0 \cdot B \cdot \left( {1 + \alpha ^2 } \right) = 1.25 \cdot P_x \hspace{0.15cm} \underline{ = 12.5\;{\rm{mW}}}.$$