Aufgabe 2.5Z: Komprimierungsfaktor vs. Restredundanz

Wir betrachten wie in Aufgabe A2.5 die Datenkomprimierung mit dem 1983 veröffentlichten Lempel–Ziv–Welch–Algorithmus. Dabei gilt:

Die Eingangsfolge habe die Länge N.

Die Länge der LZW–Coderausgabe ist L.

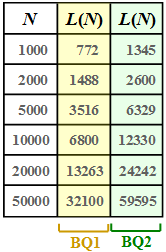
Die Grafik zeigt für zwei verschiedene binäre Nachrichtenquellen BQ1 und BQ2 den Zusammenhang zwischen den Folgenlängen N und L, dargestellt durch den Funktionsverlauf L(N). BQ1 und BQ2 besitzen die gleichen statistischen Eigenschaften wie in Aufgabe A2.5:

BQ1 ist aufgrund von ungleichen Symbolwahrscheinlichkeiten (p_A = 0.89, p_B = 0.11) redundant. Es bestehen keine Bindungen zwischen den einzelnen Symbolen. Die Entropie ist H = 0.5 bit/Quellensymbol.

BQ2 ist redundanzfrei und weist die Entropie H = 1 bit/Quellensymbol auf.

Weiter benötigen Sie für die Lösung dieser Aufagbe noch zwei Definitionen:

Der Komprimierungsfaktor ist definitionsgemäß K(N) = L(N)/N.

Die relevante Redundanz der LZW–Coderfolge (im Folgenden Restredundanz genannt) ist

$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$

Hinweis: Die Aufgabe bezieht sich auf das Kapitel 2.2.

Fragebogen

Musterlösung

1. Der Komprimierungsfaktor ist definiert als der Quotient der Längen von LZW–Ausgangsfolge (L) und Eingangsfolge (N = 10000):

$${\rm BQ1:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{6800}{10000}\hspace{0.15cm}\underline{= 0.680}\hspace{0.05cm},\\ \\ {\rm BQ2:}\hspace{0.3cm} K \hspace{0.2cm} = \hspace{0.2cm} \frac{12330}{10000}\hspace{0.15cm}\underline{= 1.233}\hspace{0.05cm}. $$

Die Lempel–Ziv–Codierung macht natürlich nur bei der redundanten Binärquelle BQ1 Sinn. Hier kann die Datenmenge um 32% gesenkt werden. Bei der redundanzfreien Binärquelle BQ2 führt dagegen die LZ–Codierung zu einer um 23.3% größeren Datenmenge.

2. Aus der angegebenen Gleichung erhält man mit N = 10000:

$${\rm BQ1:}\hspace{0.3cm} H = 0.5\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{0.5 \cdot N}{L } = 1 - \frac{5000}{6800 } \hspace{0.15cm}\underline{\approx 26.5\,\%}\hspace{0.05cm},\\ \\ {\rm BQ2:}\hspace{0.3cm} H = 1.0\hspace{0.05cm},\hspace{0.2cm} r(N=10000) \hspace{0.2cm} = \hspace{0.2cm}1 - \frac{N}{L } = 1 - \frac{10000}{12330 } \hspace{0.15cm}\underline{\approx 19\,\%}\hspace{0.05cm}.$$

Die Restredundanz gibt die (relative) Redundanz der LZ–Ausgangsfolge an. Obwohl die Quelle BQ1 für die LZ–Codierung besser geeignet ist als die redundanzfreie Quelle BQ2, ergibt sich bei BQ1 wegen der Redundanz in der Eingangsfolge eine größere Restredundanz.

Eine kleinere Restredundanz r(N) bei gegebenem N sagt also nichts darüber aus, ob der Einsatz von Lempel–Ziv für die vorliegende Quelle sinnvoll ist. Hierzu muss der Komprimierungsfaktor K betrachtet werden. Allgemein gilt folgender Zusammenhang zwischen r(N) und K(N):

$$r(N) = 1 - \frac{H}{K(N)}\hspace{0.05cm},\hspace{0.2cm} K(N) = H \cdot (1- r(N)) \hspace{0.05cm}.$$

3. Aus der Tabelle auf der Angabenseite kann man ablesen (bzw. daraus ableiten)

für die redundante Binärquelle BQ1:

$$L(N = 50000) = 32100\hspace{0.05cm},\hspace{0.2cm} K(N = 50000) = 0.642\hspace{0.05cm},\hspace{0.2cm}r(N = 50000) \hspace{0.15cm}\underline {= 22.2\,\% \hspace{0.05cm}},$$

für die redundanzfreie Binärquelle BQ2:

$$L(N = 50000) = 59595\hspace{0.05cm},\hspace{0.2cm} K(N = 50000) = 1.192\hspace{0.05cm},\hspace{0.2cm}r(N = 50000) \hspace{0.15cm}\underline {= 16.1\,\% \hspace{0.05cm}}.$$

Richtig sind somit die Aussagen 1 und 2. Für beide Quellen ist K(N = 50000) < K(N = 10000) und r(N = 50000) < r(N = 10000). In beiden Fällen ergeben sich also bei größerem N „günstigere” Werte, auch dann, wenn eigentlich wie bei der redundanzfreien Binärquelle BQ2 die Anwendung von Lempel–Ziv zu einer Verschlechterung führt.

	Bei beiden Quellen ist K(N = 50000) kleiner als K(N = 10000).
	Bei beiden Quellen ist r(N = 50000) kleiner als r(N = 10000).
	Nur bei BQ1 ergeben sich mit N = 50000 günstigere Werte.