Eigenschaften von Nyquistsystemen

Erstes Nyquistkriterium im Zeitbereich

Für dieses Kapitel wurde vorausgesetzt, dass die Detektion eines Symbols nicht durch Nachbarimpulse beeinträchtigt werden soll. Dies erreicht man durch die Detektion des Signals
\(d(t) = \sum_{(\nu)} a_\nu \cdot g_d ( t - \nu T)\) zu den Zeitpunkten νT immer dann, wenn der Detektionsgrundimpuls g_d(t)

auf den Bereich | t | < T beschränkt ist, was für das Kapitel 1.2 vorausgesetzt wurde, oder
äquidistante Nulldurchgänge zu den Zeitpunkten νT aufweist.

Aus Gründen einer möglichst einfachen Darstellung wird im Kapitel 1.3 das Detektionsstörsignal d_N(t) als vernachlässigbar klein angenommen.

: Man bezeichnet einen Detektionsgrundimpuls mit den Eigenschaften

\(g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r}}\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}...\)

als Nyquistimpuls g_Nyq(t), benannt nach dem Physiker Harry Nyquist.

: Die Grafik zeigt das Detektionssignal d(t) eines solchen Nyquistsystems. Rot gepunktet sind die (gewichteten und verschobenen) Nyquistimpulse a_ν · g_Nyq(t – νT) eingezeichnet.

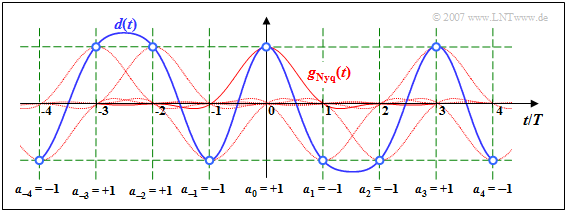
Zu den Detektionszeitpunkten gilt d(νT) = a_ν · g_Nyq(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (ν < 0) sowie die Vorläufer der nachfolgenden Impulse (ν > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols a₀ nicht.

Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls
\(g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot T}\right)\)

mit trapezförmigem Spektrum und dem Rolloff–Faktor r = 0.5 zugrunde liegt. Dieser wurde bereits im Kapitel 3 des Buches „Signaldarstellung” behandelt.