Aufgabe 1.5: Binäre Markovquelle

Die Aufgabe A1.4 hat gezeigt, dass die Berechnung der Entropie bei einer gedächtnisbehafteten Quelle sehr aufwändig sein kann. Man muss dann zunächst (sehr viele) Entropienäherungen H_k für k–Tupel berechnen und kann erst dann mit dem Grenzübergang k → ∞ die Quellenentropie ermitteln:

$$H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$

Oft tendiert dabei H_k nur sehr langsam gegen den Grenzwert H.

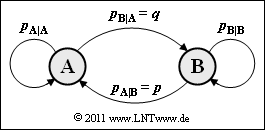
Der Rechengang wird drastisch reduziert, wenn die Nachrichtenquelle Markoveigenschaften besitzt. Die Grafik zeigt das Übergangsdiagramm für eine binäre Markovquelle mit den zwei Zuständen (Symbolen) A und B. Dieses ist durch die beiden bedingten Wahrscheinlichkeiten p_A|B = p und p_B|A = q eindeutig bestimmt. Die bedingten Wahrscheinlichkeiten p_A|A und p_B|B sowie die Symbolwahrscheinlichkeiten p_A und p_B lassen sich daraus ermitteln.

Die Entropie der binären Markovkette (mit der Einheit „bit/Symbol”) lautet dann:

$$H = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$

Bei dieser Gleichung ist zu beachten, dass im Argument des Logarithmus dualis jeweils die bedingten Wahrscheinlichkeiten p_A|A, p_B|A, ... einzusetzen sind, während für die Gewichtung die Verbundwahrscheinlichkeiten p_AA, p_AB, ... zu verwenden sind.

Mit der Entropienäherung erster Ordnung,

$$H_1 = p_{\rm A} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A}} + p_{\rm B} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B}} \hspace{0.5cm}({\rm Einheit\hspace{-0.1cm}: \hspace{0.1cm}bit/Symbol})\hspace{0.05cm},$$

sowie der oben angegebenen (tatsächlichen) Entropie H lassen sich bei einer Markovquelle auch alle weiteren Entropienäherungen (k = 2, 3, ...) direkt berechnen:

$$H_k = \frac{1}{k} \cdot [ H_{\rm 1} + (k-1) \cdot H_{\rm M}] \hspace{0.05cm}.$$

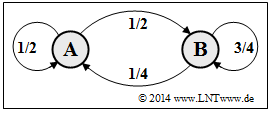
Hinweis: Diese Aufgabe gehört zum Themengebiet von Kapitel 1.2. Mit Ausnahme der Teilaufgabe (6) sei p = 1/4 und q = 1/2.

Für die (ergodischen) Symbolwahrscheinlichkeiten einer Markovkette erster Ordnung gilt:

$$ p_{\rm A} = \frac {p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}, \hspace{0.3cm} p_{\rm B} = \frac {p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} { p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} + p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} \hspace{0.05cm}.$$

Fragebogen

$p = 1/4,\ q = 1/2:\ p_\text{A|A}$ =

$p_\text{B|B}$ =

$p = 1/4,\ q = 1/2:\ p_A$ =

$p_B$ =

$p = 1/4,\ q = 1/2:\ H_1$ =

$bit/Symbol$

$p = 1/4,\ q = 1/2:\ H$ =

$bit/Symbol$

$p = 1/4,\ q = 1/2:\ H_2$ =

$bit/Symbol$

$H_3$ =

$bit/Symbol$

$H_4$ =

$bit/Symbol$

$p = 1/4,\ q = 1/2:\ H$ =

$bit/Symbol$

Musterlösung

1. Hier gilt für die Übergangswahrscheinlichkeiten:

$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}= 1 - q \hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm},\\ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.1cm} = \hspace{0.1cm} 1 - p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}= 1 - p \hspace{0.15cm} \underline {= 0.75} \hspace{0.05cm}.$$

Nach A sind A und B gleichwahrscheinlich. Nach B tritt B sehr viel häufiger als A auf.

2. Entsprechend den angegebenen Gleichungen gilt:

$$p_{\rm A}= \frac{p}{p+q} = \frac{0.25}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.333} \hspace{0.05cm}, \hspace{2cm}$$

$$ p_{\rm B} = \frac{q}{p+q} = \frac{0.50}{0.25 + 0.50} \hspace{0.15cm} \underline {= 0.667} \hspace{0.05cm}.$$

3. Mit den unter (b) berechneten Wahrscheinlichkeiten gilt:

$$H_{\rm 1} = H_{\rm bin}(p_{\rm A}) = 1/3 \cdot {\rm log}_2\hspace{0.01cm} (3) + 2/3 \cdot {\rm log}_2\hspace{0.01cm} (1.5) = 1.585 - 2/3\hspace{0.15cm} \underline {= 0.918 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

4. Die Entropie der Markovquelle lautet entsprechend der Angabe

$$H = p_{\rm AA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$

Für die Verbundwahrscheinlichkeiten gilt:

$$p_{\rm AA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = (1-q) \cdot \frac{p}{p+q} = \frac{1/2 \cdot 1/4}{3/4} = \frac{1}{6} \hspace{0.05cm},\\ p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} = q \cdot \frac{p}{p+q} = \frac{1/2 \cdot 1/4}{3/4} = \frac{1}{6} \hspace{0.05cm},\\ p_{\rm BA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = p \cdot \frac{q}{p+q} = p_{\rm AB} = \frac{1}{6} \hspace{0.05cm},\\ p_{\rm BB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = (1-p) \cdot \frac{q}{p+q} = \frac{3/4 \cdot 1/2}{3/4} = \frac{1}{2} $$

$$\Rightarrow\hspace{0.3cm} H \hspace{0.1cm} = \hspace{0.1cm} 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (2) + 1/6 \cdot {\rm log}_2\hspace{0.01cm} (4) + 1/2 \cdot {\rm log}_2\hspace{0.1cm} (4/3) = \\ \hspace{0.1cm} = \hspace{0.1cm} 1/6 + 1/6 + 2/6 + 1 - 1/2 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.875 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

5. Allgemein gilt mit H_M = H für die k–Entropienäherung:

$$H_k = \frac{1}{k} \cdot [ H_{\rm 1} + (k-1) \cdot H_{\rm M}] \hspace{0.05cm}.$$

Daraus folgt:

$$H_2 \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{2} \cdot [ 0.918 + 1 \cdot 0.875] \hspace{0.15cm} \underline {= 0.897 \,{\rm bit/Symbol}} \hspace{0.05cm},\\ H_3 \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{3} \cdot [ 0.918 + 2 \cdot 0.875] \hspace{0.15cm} \underline {= 0.889 \,{\rm bit/Symbol}} \hspace{0.05cm},\\ H_4 \hspace{0.1cm} = \hspace{0.1cm} \frac{1}{4} \cdot [ 0.918 + 3 \cdot 0.875] \hspace{0.15cm} \underline {= 0.886 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

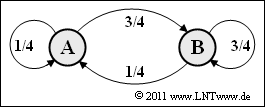
6. Mit dem neuen Parametersatz (p = 1/4, q = 3/4) erhält man für die Symbolwahrscheinlichkeiten: p_A = 1/4 und p_B = 3/4. Dieser Sonderfall führt demnach zu statistisch unabhängigen Symbolen:

$$ p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B} \hspace{0.05cm}.$$

Damit ist die Entropie H identisch mit der Entropienäherung H₁:

$$H = H_{\rm 1} = 1/4 \cdot {\rm log}_2\hspace{0.01cm} (4) + 3/4 \cdot {\rm log}_2\hspace{0.01cm} (4/3) = 2 - 0.75 \cdot {\rm log}_2\hspace{0.01cm} (3) \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$

Die Entropienäherungen H₂, H₃, H₄, ... liefern hier ebenfalls das Ergebnis 0.811 bit/Symbol.